ここでは【数学C】複素数平面でよく利用する公式(基礎知識)や例題を一覧にしてまとめています。
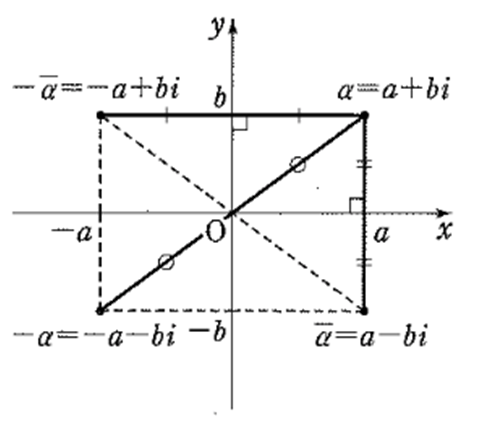
1.共役な複素数の性質
\(z, \alpha, \beta\) は複素数, \(\alpha =a + bi\) とする。
① \(z\) が実数 ⇔ \(\color{red}{\overline{z} = z}\)
② \(z\) が純虚数 ⇔ \(\color{red}{\overline{z} = – z, z \neq 0}\)
① \(\color{red}{\alpha + \overline{\alpha} = 2a}\)
② \(\color{red}{\alpha \overline{\alpha} = a^2 + b^2}\)
③ \(\color{red}{\overline{\overline{\alpha}} = \alpha}\) ⇐共役な複素数のバーは2回で外れる
① \(\color{red}{\overline{\alpha + \beta} = \overline{\alpha} + \overline{\beta}}\)
② \(\color{red}{\overline{\alpha – \beta} = \overline{\alpha}}\) \(\color{red}{-}\) \(\color{red}{\overline{\beta}}\)
③ \(\color{red}{\overline{\alpha \beta} = \overline{\alpha}}\) \(\color{red}{\overline{\beta}}\)
特に、\(\color{red}{\overline{\alpha^n} = (\overline{\alpha})^n}\)
④ \(\color{red}{\overline{\left( \displaystyle\frac{\alpha}{\beta} \right)} = \displaystyle\frac{\overline{\alpha}}{\overline{\beta}}}\)
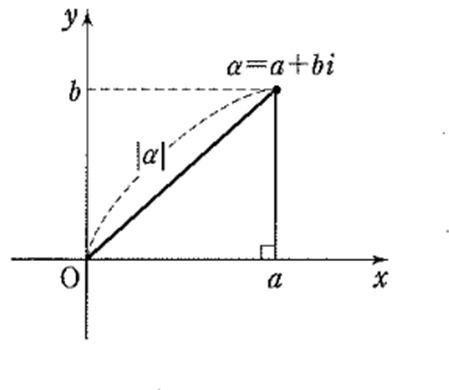
2.複素数の絶対値(大きさ)
\(\alpha, z\)は複素数であり、 \(\alpha = a + bi\) とする
\(|\alpha| = |a + bi| = \color{red}{\sqrt{a^2 + b^2}}\)
例題
\(\alpha = 2 + 3i\) のとき,\(|\alpha|\) の値を求めよ。
解答
\(|\alpha| = \sqrt{2^2 + 3^2} =\sqrt{13}\)
① \(|\alpha| = |\overline{\alpha}| = |- \alpha|\)
② \(\color{red}{z\overline{z} = |z|^2} \)
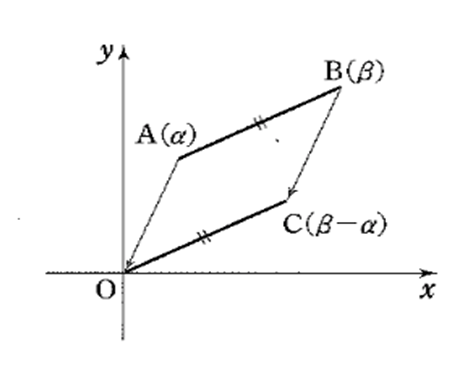
3.複素数の演算と図示
\(\alpha, \beta\) は複素数とする。
\(\alpha = a + bi , \beta = c + di\) のとき
2点 \(\alpha , \beta\) 間の距離は \(|\beta – \alpha| = \color{red}{\sqrt{(c – a)^2 + (d – b)^2}}\)
例題
2点\(\alpha = 2+ i , \beta = 3 – 2i\) 間の距離を求めよ。
解答
\(|\beta – \alpha| = \sqrt{( 3 – 2)^2 + (-2 – 1)^2} = \sqrt{10}\)
\(a \neq 0\) のとき
3点 \(0, \alpha, \beta\) が一直線上にある ⇔ \(\color{red}{\beta = k\alpha}\) となる実数 \(k\) がある
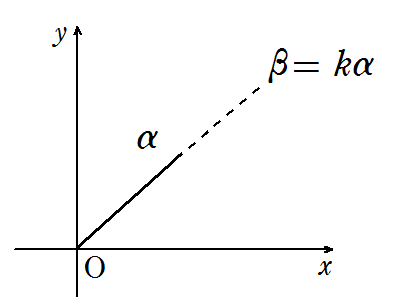
例題
\(\alpha = a – i, \beta = 8 + 4i\) とする。
\(3\) 点\(O, \alpha , \beta\) が一直線上にあるとき,\(a\) を求めよ。
解答
\(3\) 点\(O, \alpha , \beta\) が一直線上にあるとき,
\(\beta = k \alpha. (k:実数)\)
と表せるから,
\(8 + 4i = k (a – i)\)
\(8 + 4i = ka – ki)\)
よって,\(8 = ka , 4 = -k\)
したがって,\(k = -4, a = -2\)
4.複素数の極形式
\(\alpha, \beta, z\) は複素数とする。
\( \alpha = r_1 (\cos \theta_1 + i \sin \theta_1 ), \beta = r_2 (\cos \theta_2 + i \sin \theta_2 )\) のとき
① \(\color{red}{\alpha \beta = r_1 r_2 \{\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)\}}\)
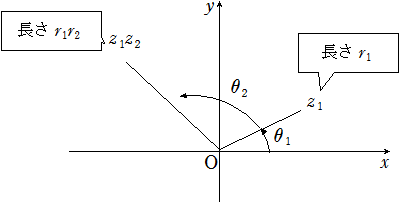
② \(\color{red}{\displaystyle\frac{\alpha}{\beta} = \displaystyle\frac{r_1}{r_2}\{\cos(\theta_1 – \theta_2) + i\sin(\theta_1 – \theta_2) \}}\)
例題
\(z_1 = r(\cos\theta + i\sin\theta)\) , \(z_2 = \cos\displaystyle\frac{\pi}{6} + i\sin\displaystyle\frac{\pi}{6}\) のとき,\(z_1 z_2\) を求めよ。
解答
\(z_1 z_2 = r(\cos\theta + i\sin\theta) \times \left(\cos\displaystyle\frac{\pi}{6} + i\sin\displaystyle\frac{\pi}{6}\right)\)
\(= r\left\{\cos\left(\theta + \displaystyle\frac{\pi}{6}\right) +i\sin\left(\theta + \displaystyle\frac{\pi}{6}\right) \right\}\)
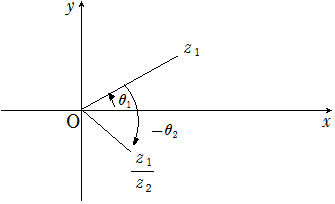
① \(\color{red}{|\alpha \beta| = |\alpha||\beta| , arg\alpha \beta = arg\alpha + arg\beta}\)
② \(\color{red}{\left|\displaystyle\frac{\alpha}{\beta}\right| = \displaystyle\frac{|\alpha|}{|\beta|} , arg\displaystyle\frac{\alpha}{\beta} = arg\alpha – arg\beta}\)
例題
\(z_1 =\left( \cos\displaystyle\frac{\pi}{3} + i\sin\displaystyle\frac{\pi}{3}\right)\) , \(z_2 = 2\left(\cos\displaystyle\frac{\pi}{6} + i\sin\displaystyle\frac{\pi}{6}\right)\) のとき,\(|z_1 z_2|\) を求めよ。また,\(z_1 z_2\) の偏角を求めよ。
解答
\(|z_1| = 1\) , \(|z_2| = 2\) より\(|z_1 z_2| = |z_1||z_2| = 1 \cdot 2 = 2 \)
\(arg z_1 = \displaystyle\frac{\pi}{3}, arg z_2 = \displaystyle\frac{\pi}{6}\)より\(arg z_1 z_2 = arg z_1 + arg z_2 = \displaystyle\frac{\pi}{3} + \displaystyle\frac{\pi}{6} = \displaystyle\frac{\pi}{2}\)
\(\alpha = \cos\theta + i\sin\theta\) と\(z\) に対して, 点 \(\alpha z\) は, 点 \(z\) を原点を中心として\(\theta\)だけ回転した点である。
例題
点\(z = 1 + i\) を原点を中心として\(\displaystyle\frac{\pi}{3}\) だけ回転した点を求めよ。
解答
\(z \cdot \left(\cos\displaystyle\frac{\pi}{3} + i \sin\displaystyle\frac{\pi}{3}\right)\)
\(= (1 + i)\left(\displaystyle\frac{1}{2} + \displaystyle\frac{\sqrt{3}}{2}i\right)\)
\(= \left(1 – \displaystyle\frac{\sqrt{3}}{2}\right) + \left(\displaystyle\frac{1}{2} + \displaystyle\frac{\sqrt{3}}{2}\right)i\)
5.ド・モアブルの定理
\(n\) が整数のとき
\(\color{red}{(\cos\theta + i\sin\theta)^n = \cos n\theta + i\sin n\theta}\)
例題
\(\left(\cos\displaystyle\frac{\pi}{3} + i\sin\displaystyle\frac{\pi}{3}\right)^4 \) を計算せよ。
解答
\(\left(\cos\displaystyle\frac{\pi}{3} + i\sin\displaystyle\frac{\pi}{3}\right)^4 \)
\(= \cos\displaystyle\frac{4}{3}\pi + i\sin\displaystyle\frac{4}{3}\pi \)
\(= -\displaystyle\frac{1}{2} -\displaystyle\frac{\sqrt{3}}{2}i\)
自然数 \(n\) に対して, \(1\) の\(n\) 乗根は,次の\(n\) 個の複素数になる
\(\color{red}{z_k = \cos\displaystyle\frac{2k\pi}{n} + i\sin\displaystyle\frac{2k\pi}{n}} \)
\((k = 0, 1, 2, \cdots, n – 1)\)
例題
\(1\) の\(6\) 乗根を表す複素数を求めよ。
解答
\(z_k = \cos\displaystyle\frac{2k\pi}{6} + i\sin\displaystyle\frac{2k\pi}{6}\) \((k = 0, 1, 2, \cdots, 5)\)
より
\(z_0 = 1\)
\(z_1 = \cos\displaystyle\frac{2\pi}{6} + i\sin\displaystyle\frac{2\pi}{6} = \displaystyle\frac{1}{2} + \displaystyle\frac{\sqrt{3}}{2}i\)
\(z_2 = \cos\displaystyle\frac{4\pi}{6} + i\sin\displaystyle\frac{4\pi}{6} = -\displaystyle\frac{1}{2} + \displaystyle\frac{\sqrt{3}}{2}i\)
\(z_3 = \cos\displaystyle\frac{6\pi}{6} + i\sin\displaystyle\frac{6\pi}{6} = -1\)
\(z_4 = \cos\displaystyle\frac{8\pi}{6} + i\sin\displaystyle\frac{8\pi}{6} = -\displaystyle\frac{1}{2} – \displaystyle\frac{\sqrt{3}}{2}i\)
\(z_5 = \cos\displaystyle\frac{10\pi}{6} + i\sin\displaystyle\frac{10\pi}{6} = \displaystyle\frac{1}{2} – \displaystyle\frac{\sqrt{3}}{2}i\)
6.複素数と図形
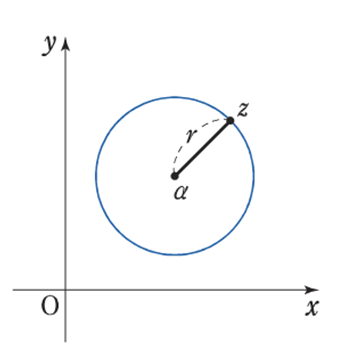
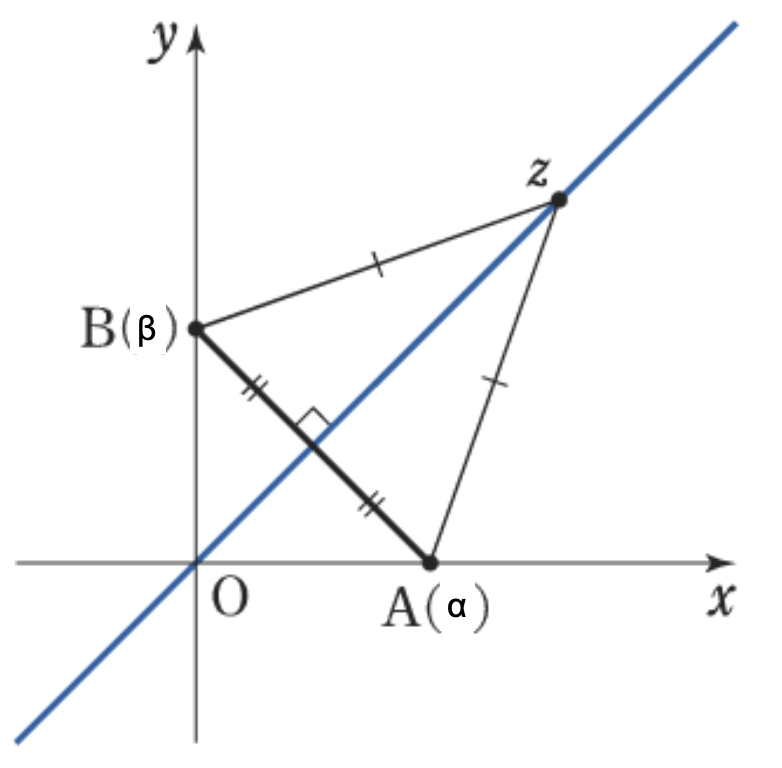
\(A(\alpha)\),\(B(\beta)\),\(C(\gamma)\) とする。
\(|z – \alpha| = \gamma \) ⇒ 点 A を中心とする半径\(r\) の円
\(|z – \alpha| = |z – \beta| \) ⇒ 線分 AB の垂直二等分線
例題
次の方程式を満たす点\(z\) 全体はどのような図形か。
(1)\(|z – 1 + i| = 3 \)
(2) \(|z – 1| = |z – i| \)
解答
(1)\(|z – (1 – i)| = 3 \) より 中心が点 \(1 – i\) , 半径\(3\) の円
(2) 点\(A(1)\), \(B(i)\) を結ぶ線分の垂直二等分線
点 \(\beta\) を, 点\(\alpha\) を中心として角\(\theta\) だけ回転した点を\(\gamma\) とすると
\(\color{red}{\gamma – \alpha = (\cos\theta + i\sin\theta)(\beta – \alpha)}\)
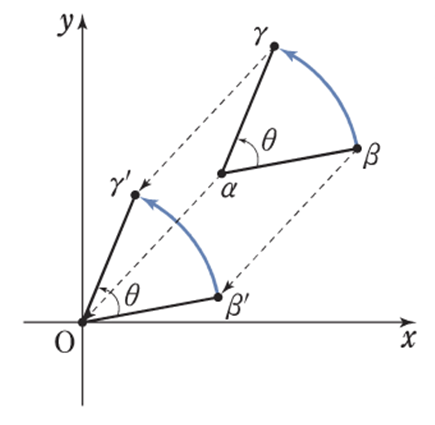
例題
\(\alpha = 2 + 3i, \beta = 4 + i \) とするとき,点\(\beta\) を点\(\alpha\) を中心として\(\displaystyle\frac{\pi}{6}\) だけ回転した点を表す複素数\(\gamma\) を求めよ。
解答
\(\gamma – \alpha = \left(\cos\displaystyle\frac{\pi}{6} + i\sin\displaystyle\frac{\pi}{6}\right)(\beta – \alpha)\)
より
\(\gamma = \left(\displaystyle\frac{\sqrt{3}}{3} + \displaystyle\frac{1}{2}i \right)\left\{(4 + i) – (2 + 3i)\right\} + (2 + 3i)\)
\(= (3 + \sqrt{3}) + (4 – \sqrt{3})i\)
\(A(\alpha), B(\beta), C(\gamma)\) について
半直線 AB から半直線 AC までの回転角\(\theta\) は
\(\color{red}{\theta = arg\displaystyle\frac{\gamma – \alpha}{\beta – \alpha}}\)
例題
\(\alpha = 1 – 2i, \beta = -i , \gamma = (1 + \sqrt{3}) – (2 – \sqrt{3})i\) のときの\(\angle \beta\alpha\gamma\) の値を求めよ。(ただし,\(-\pi < \angle \beta\alpha\gamma \leq \pi\))
解答
\(\displaystyle\frac{\gamma – \alpha}{\beta – \alpha}\)
\(= \displaystyle\frac{\sqrt{3} + \sqrt{3}i}{-1 + i}\)
\(= -\sqrt{3}i\)
\(= \sqrt{3}\left\{ \cos\left(-\displaystyle\frac{\pi}{2}\right) + i\sin\left(-\displaystyle\frac{\pi}{2}\right)\right\}\)
よって、 \(\angle \beta\alpha\gamma = arg\displaystyle\frac{\gamma – \alpha}{\beta – \alpha} = -\displaystyle\frac{\pi}{2}\)





コメント