ここでは【数学C】式と曲線でよく利用する基本公式(基礎知識)や例題を一覧にしてまとめています。
1.放物線
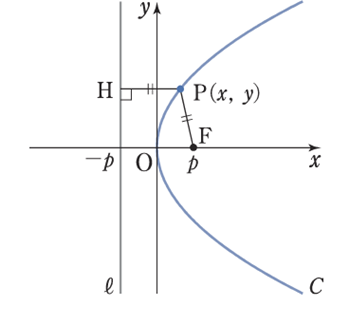
定点 \(F\) と\(F\) を通らない定直線 \(\ell\) からの距離が等しい点\(P\) の軌跡
※この定点\(F\) を焦点、定直線 \(\ell\)を準線という。
\(x\) 軸を軸とする放物線について
① 方程式は \(\color{red}{y^2 = 4px (p \neq 0)}\)
② 頂点は原点, 軸は\(x\) 軸
(曲線は軸に関して対称)
③ 焦点は\((\color{red}{F(p, 0)}\) , 準線は直線 \(\color{red}{x = -p}\)
例題
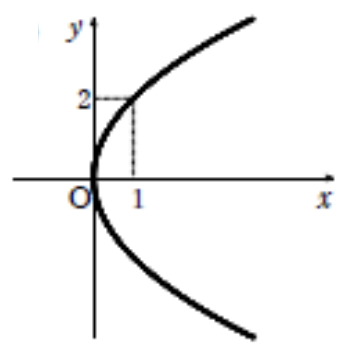
焦点が点\((1, 0)\) ,準線が直線\(x = -1\) である放物線の方程式を求め,概形をかけ。
解答
\(y^2 = 4 \cdot 1 \cdot x\) より\(y^2 = 4x\)
2.楕円
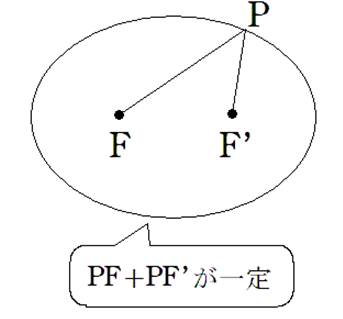
2定点\(F, F’\) からの距離の和が一定である点\(P\)の軌跡
(ただし、\(PF + PF’ > FF’\))
※2定点 \(F, F’\) を焦点という
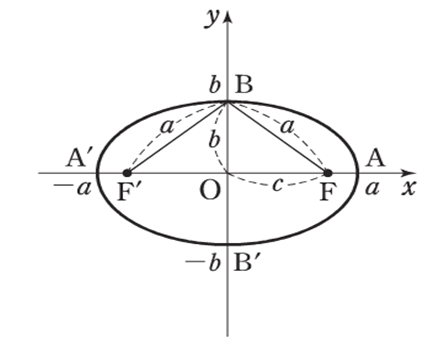
長軸の長さ(AA’) が \(2a\), 短軸の長さ(BB’)が \(2b\) の楕円について
① 方程式は
\(\color{red}{\displaystyle\frac{x^2}{a^2} + \displaystyle\frac{y^2}{b^2} = 1}\)
② 焦点は
\(\color{red}{F(\sqrt{a^2 – b^2} , 0), F'(-\sqrt{a^2 – b^2} , 0)}\)
④ 頂点は
\((a, 0), (-a, 0), (0, b), (0, -b)\)
③ 楕円上の点から 2 つの焦点までの和は
\(\color{red}{2a}\)
例題
方程式が\(\displaystyle\frac{x^2}{16} + \displaystyle\frac{y^2}{4} = 1\) である楕円の長軸の長さ,短軸の長さ,焦点および頂点を求めよ。また,楕円の概形をかけ。
解答
\(\displaystyle\frac{x^2}{4^2} + \displaystyle\frac{y^2}{2^2} = 1\) より
長軸の長さは \(2 \cdot 4 = 8\)
短軸の長さは \(2 \cdot 2 = 4\)
\(\sqrt{16 – 4} = 2\sqrt{3}\)より
焦点は2点\((2\sqrt{3}, 0)\),\((-2\sqrt{3}, 0)\)
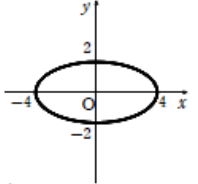
頂点は\((4, 0)\), \((-4, 0)\), \((0, 2)\), \((0, -2)\)
概形は以下になる
3.双曲線
2定点\(F, F’\) からの距離の差が一定である点\(P\)の軌跡
※2定点 \(F, F’\) を焦点という
\(|PF – PF’|\)が一定
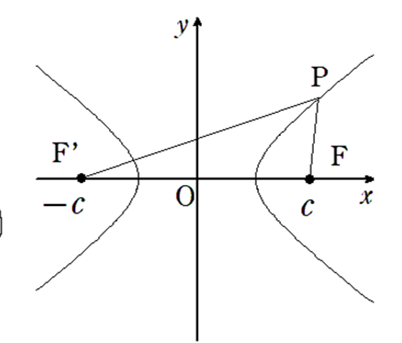
2定点 \(F(c, 0), F'(-c, 0)\) を焦点とし、定点からの距離の差が \(2a\) である双曲線について
① 方程式は
\(\color{red}{\displaystyle\frac{x^2}{a^2} – \displaystyle\frac{y^2}{b^2} = 1}\)
② 焦点は
\(\color{red}{F(\sqrt{a^2 + b^2} , 0), F'(-\sqrt{a^2 + b^2} , 0)}\)
※\(\color{red}{c = \sqrt{a^2 + b^2}}\)
③ 双曲線上の点から 2 つの焦点までの差は
\(\color{red}{2a}\)
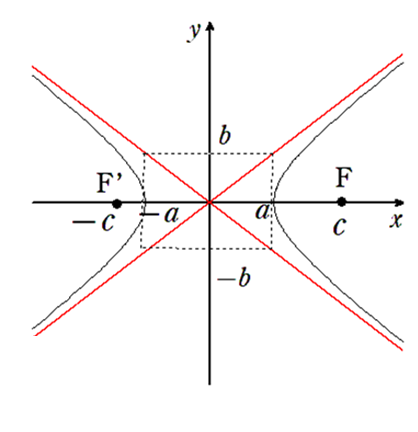
④ 頂点は \((a, 0), (-a, 0)\)
⑤ 漸近線の方程式は
直線 \(\color{red}{y = \displaystyle\frac{b}{a}x, y = -\displaystyle\frac{b}{a}x}\)
例題
方程式が\(\displaystyle\frac{x^2}{9} – \displaystyle\frac{y^2}{16} = 1\) である双曲線の頂点,焦点,および漸近線を求めよ。また,双曲線の概形をかけ。
解答
\(\displaystyle\frac{x^2}{3^2} – \displaystyle\frac{y^2}{4^2} = 1\) より
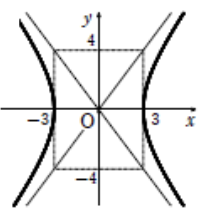
頂点:\((3, 0), (-3, 0)\)
\(\sqrt{9 + 16} = 5\) より
焦点:\((5, 0), (-5, 0)\)
漸近線:2直線\(\displaystyle\frac{x}{3} – \displaystyle\frac{y^2}{4} = 0, \displaystyle\frac{x}{3} + \displaystyle\frac{y^2}{4} = 0\)
4.曲線の平行移動
曲線\(F(x, y) = 0\) を\(x\) 軸方向に\(p\), \(y\) 軸方向に\(q\) だけ平行移動して得られる曲線の方程式は
\(\color{red}{F(x – p, y – q) = 0}\) ←通常の平行移動と同じ
例題
方程式が\(\displaystyle\frac{x^2}{4} – \displaystyle\frac{y^2}{9} = 1\)である曲線を,\(x\) 軸方向に\(3\), \(y\) 軸方向に\(5\) だけ平行移動して得られる曲線の方程式を求めよ。
解答
\(\displaystyle\frac{(x – 3)^2}{4} – \displaystyle\frac{(y – 5)^2}{9} = 1\)
5.2次曲線と直線の共有点
2次曲線と直線の方程式から1文字を消去して2次方程式が得られる場合,その2次方程式の実数解の個数と,2次曲線と直線の共有点の個数は一致する。
例題
\(k\) は定数とするとき,曲線\(x^2 – 2y^2 = 8 \cdots ①\)と直線 \(y = x + k \cdots ②\) の共有点の個数を調べよ。
解答
②を①に代入すると
\(x^2 – 2(x + k)^2 = 8\)
\(x^2 – 2x^2 – 4kx – 2k^2 = 8\)
\(x^2 + 4kx + 2k^2 + 8 = 0\)
この2次方程式の判別式を\(D\) とすると
\(\displaystyle\frac{D}{4} = (2k)^2 – (2k^2 + 8) = 2k^2 – 8 = 2(k + 2)(k – 2)\)
よって,曲線①と直線②の共有点の個数は,次のようになる。
\(D > 0\) すなわち \(k < -2, 2 < k\) のとき 共有点は\(2\)個
\(D = 0\) すなわち \(k = \pm 2\) のとき 共有点は\(1\)個
\(D < 0\) すなわち \(-2 < k < 2\) のとき 共有点は\(0\)個
6.2次曲線と接線
① 放物線\(y^2 =4px\) 上の点\((x_1 , y_1)\) における接線の方程式は
\(\color{red}{y_1y = 2p(x + x_1)}\)
② 楕円\(\displaystyle\frac{x^2}{a^2} + \displaystyle\frac{y^2}{b^2} = 1\)上の点\((x_1 , y_1)\) における接線の方程式は
\(\color{red}{\displaystyle\frac{x_1x}{a^2} + \displaystyle\frac{y_1y}{b^2} = 1}\)
③ 双曲線\(\displaystyle\frac{x^2}{a^2} – \displaystyle\frac{y^2}{b^2} = 1\)上の点\((x_1 , y_1)\) における接線の方程式は
\(\color{red}{\displaystyle\frac{x_1x}{a^2} – \displaystyle\frac{y_1y}{b^2} = 1}\)
例題
楕円\(\displaystyle\frac{x^2}{2} + \displaystyle\frac{y^2}{8} = 1\)上の点\((1 , 2)\) における接線の方程式を求めよ。
解答
\(\displaystyle\frac{1 \cdot x}{2} + \displaystyle\frac{2 \cdot y}{8} = 1\) より
\(\displaystyle\frac{x}{2} + \displaystyle\frac{y}{4} = 1\)
7.離心率と準線
定点\(F\) と, \(F\) を通らない定直線\(ell\) からの距離の比が \(e : 1\) である点の軌跡は
① \(0 < e < 1\) のとき \(F\) を焦点の1つとする楕円
② \(e = 1\) のとき \(F\) を焦点, \(\ell\) を準線とする放物線
③ \(e > 1\) のとき \(F\) を焦点の1つとする双曲線
※\(e\) を離心率という。
8.曲線の媒介変数表示
① 放物線 \(y^2 = 4px\)
→ \(\color{red}{x = pt^2, y = 2pt}\)
② 円 \(x^2 + y^2 = a^2\)
→ \(\color{red}{x = a\cos\theta, y = a\sin\theta}\)
③ 楕円 \(\displaystyle\frac{x^2}{a^2} + \displaystyle\frac{y^2}{b^2} = 1\)
→ \(\color{red}{x = a\cos\theta, y = b\sin\theta}\)
④ 双曲線 \(\displaystyle\frac{x^2}{a^2} – \displaystyle\frac{y^2}{b^2} = 1\)
→ \(\color{red}{x = \displaystyle\frac{a}{\cos\theta}, y = b\tan\theta}\)
⑤ サイクロイド
→ \(x = a(\theta – \sin\theta), y = a(1 – \cos\theta)\)
※\(p \neq 0 , a > 0, b > 0\)
例題
次の方程式を角\(\theta\) を媒介変数として表せ。
(1)\(y^2 = 8x\)
(2)\(x^2 + y^2 = 4\)
(3)\(\displaystyle\frac{x^2}{9} + \displaystyle\frac{y^2}{4} = 1\)
(4)\(\displaystyle\frac{x^2}{16} – \displaystyle\frac{y^2}{9} = 1\)
解答
(1)\(x = 2t^2, y = 4t\)
(2)\(x = 2\cos\theta, y = 2\sin\theta\)
(3)\(x = 3\cos\theta, y = 2\sin\theta\)
(4)\(x = \displaystyle\frac{4}{\cos\theta}, y = 3\tan\theta\)
曲線 \(x = f(t), y = g(t)\) を,\(x\)軸方向に\(p\) ,\(y\)軸方向に\(q\) だけ平行移動した曲線は
\(\color{red}{x = f(t) + p , y = g(t) + q} \)
例題
\(x = 2\cos\theta , y = 2\sin\theta\) を\(x\)軸方向に\(5\) ,\(y\)軸方向に\(3\) だけ平行移動した曲線の方程式を求めよ。
解答
\(x = 2\cos\theta + 5 , y = 2\sin\theta + 3\)
9.極座標と極方程式
① \(\color{red}{x = r\cos\theta , y = r\sin\theta}\)
② \(\color{red}{r = \sqrt{x^2 + y^2}}\)
\(r \neq 0\) のとき \(\cos\theta = \displaystyle\frac{x}{r}, \sin\theta = \displaystyle\frac{y}{r}\)
例題
直交座標が\((-3, 3)\) であるような極座標\((r, \theta)\) を求めよ。ただし,\(0 \leq \theta < 2\pi \) とする。
解答
\(x = 0 , y = -3\) より
\(r = \sqrt{0^2 + (-3)^2} = 3\)
\(\cos\theta = \displaystyle\frac{x}{r} = 0\)
\(\sin\theta = \displaystyle\frac{y}{r} = -1\)
\(0 \leq \theta < 2\pi \) より \(\theta = \displaystyle\frac{3}{2}\pi \)
よって、求める極座標は \(\left(3, \displaystyle\frac{3}{2}\pi \right)\)
① 中心が極\(O\), 半径が\(a\) の円の極方程式は
\(\color{red}{r = a}\)
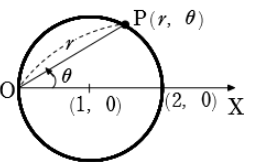
② 中心の極座標が\((a, 0)\), 半径が\(a\) の円の極方程式は
\(\color{red}{r = 2a\cos\theta}\)
③ 中心の極座標が\((r_1, \theta_1)\), 半径が\(a\)の円の極方程式は
\(\color{red}{r^2 + r_1{}^2 – 2rr_1 \cos(\theta – \theta_1) = a^2}\)
例題
次の極方程式で表される曲線を求めよ。
(1)\(r = 1\)
(2)\(r = 2\cos\theta\)
解答
(1)極Oを中心とし,半径が1の円
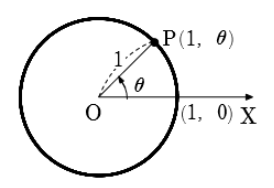
(2)中心の極座標が\((1, 0)\) ,半径\(1\)の円
① 極\(O\) を通り, 始線とのなす角が\(\alpha\) である直線の極方程式は
\(\color{red}{\theta = \alpha}\)
② \(A(r_1, \theta_1)\) を通り, OA に垂直な直線の極方程式は
\(\color{red}{r\cos(\theta – \theta_1) = r_1}\)
※\(r_1 > 0\)
例題
次の極方程式で表される曲線を求めよ。
(1)\(\theta = \displaystyle\frac{\pi}{6}\)
(2)\(r\cos(\theta – \displaystyle\frac{\pi}{3}) = 2\)
解答
(1)極O を通り,始線とのなす角が\(\displaystyle\frac{\pi}{6}\) の直線
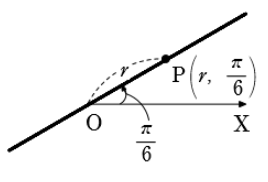
(2)極座標が\(\left(2, \displaystyle\frac{\pi}{3}\right)\) である点A を通り,OAに垂直な直線
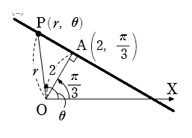
極座標が\((a, 0)\) である点を通り,始線 OX に垂直な直線を\(\ell\) とすると、次の極方程式は2次曲線を表す。
\(r = \displaystyle\frac{ea}{1 + e\cos\theta}\)
① \(0 < e < 1\) のとき \(O\) を焦点の1つとする楕円
② \(e = 1\) のとき \(O\) を焦点, \(\ell\) を準線とする放物線
③ \(e > 1\) のとき \(O\) を焦点の1つとする双曲線





コメント