【数学Ⅲ】関数～基本公式・例題一覧～

①　定義域は\(x \neq p\), 値域は\(y \neq q\)

②　漸近線は\(x = 0\) (\(y\) 軸), \(y = 0\) (\(x\) 軸)

③ グラフの存在範囲は　
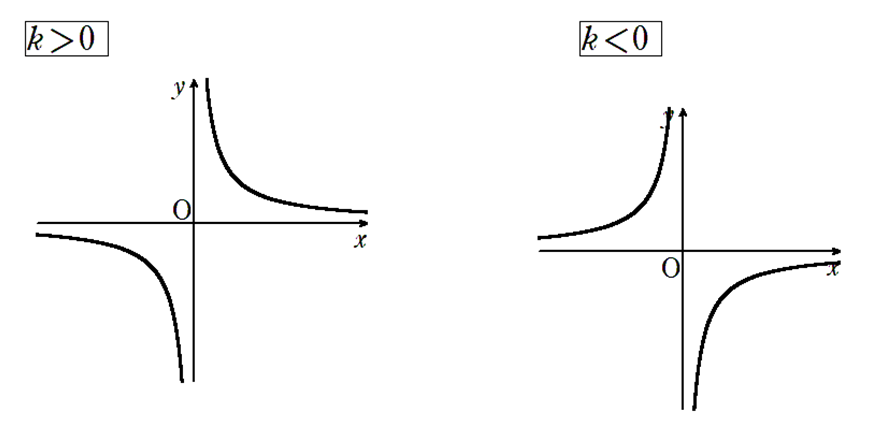
\(k > 0\) のとき第1象限、第3象限
\(k < 0\) のとき第2象限、第4象限

④　グラフは原点対称

⑤　概形は直角双曲線（漸近線が直交している）

例題

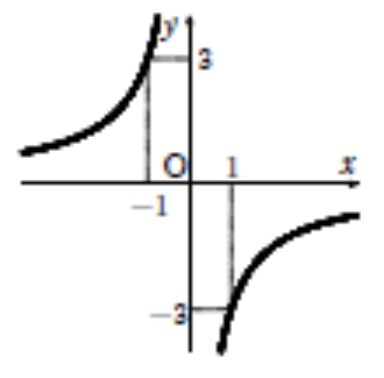
関数\(y = – \displaystyle\frac{3}{x}\) のグラフをかけ。

解答

①　\(y = \displaystyle\frac{k}{x}\) を \(x\) 軸方向\(p\) , \(y\) 軸方向\(q\) だけ平行移動したグラフ

②　漸近線は \(x = p , y = q\)

③　定義域は \(x \neq p\), 値域は\(y \neq q\)

例題

関数\(y = -\displaystyle\frac{1}{x – 1} + 2\) のグラフをかけ。また，その定義域と値域を求めよ。

解答

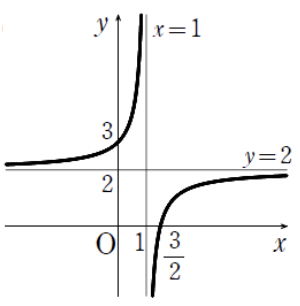
定義域：\(x \neq 1, y \neq2\)

\( y = \displaystyle\frac{ax + b}{cx + d}\) のグラフ 　⇒　　\( y = \displaystyle\frac{k}{x – p} + q\) に変形する

例題

関数\(y = \displaystyle\frac{4x + 3}{2x – 1}\) のグラフをかけ。また，その定義域と値域を求めよ。

解答

\(y = \displaystyle\frac{4x + 3}{2x – 1}\)

\(= \displaystyle\frac{2(2x – 1) + 5}{2x – 1}\)

\(= \displaystyle\frac{5}{2x – 1} + 2\)

より、グラフは以下になる

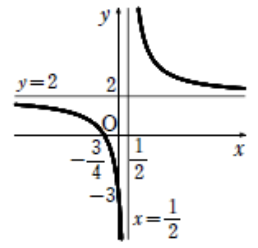
定義域：\(x \neq \displaystyle\frac{1}{2}\)

値域：\(y \neq 2\)

\(a > 0\) のとき

①　定義域：\(x \geq 0\), 値域：\(y \geq 0\)

②　グラフは単調増加

③　概形は\(y^2 = x\) の上側\(x \geq 0, y \geq 0\) の部分

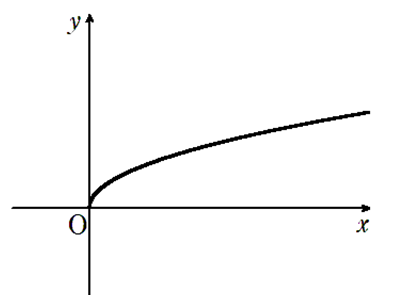
例題

関数\(y = -\sqrt{2x}\) のグラフをかけ。また，その定義域と値域を求めよ。

解答

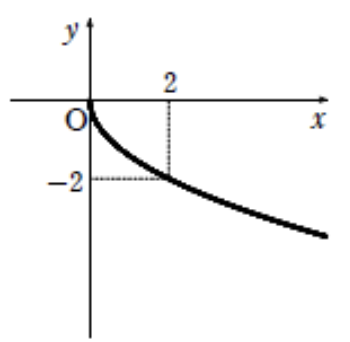
定義域：\(x \geq 0\)

値域：\(y \leq 0\)

無理関数\(y = \sqrt{a(x – p)}\) のグラフは

①　\(y = \sqrt{ax}\)のグラフを\(x\) 軸方向に\(p\) だけ平行移動したグラフ

②　定義域と値域は
・\(a > 0\) のとき、定義域：\(x \geq p\) , 値域：\(y \geq 0\)
・\(a < 0\) のとき、定義域：\(x \leq p\) , 値域：\(y \geq 0\)

例題

関数\(y = \sqrt{2x + 4}\) のグラフをかけ。また，その定義域と値域を求めよ。

解答

\(\sqrt{2x + 4} = \sqrt{2(x + 2)}\)

より、グラフは以下のようになる

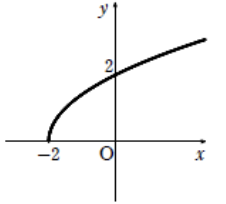
定義域：\(x \geq -2\)

値域：\(y \geq 0\)

関数\(f(x)\) が逆関数 \(f^{-1}(x)\) をもつとき

①　\(b = f(a) \iff a = f^{-1}(b)\)

②　\(f(x)\) と \(f^{-1}(x)\) では、定義域と値域が入れ替わる

③　\(y = f(x)\) のグラフと\(y = f^{-1}(x)\) のグラフは直線\(y = x\) に関して対称

\(f(x)\) の値域が \(g(x)\) の定義域に含まれているとき

\((g \circ f) (x) = g(f(x))\)

①　一般に\((g \circ f) (x)\) と \((f \circ g) (x)\) は一致しない。

②　\(f(x)\) の逆関数が \(g(x)\) のとき,それぞれの定義域で
\((f \circ g) (x) = x\) , \((g \circ f) (x) = x\)