ここでは、【数学C】でよく利用する公式を一覧にしてまとめています。
【数学C】ベクトル~公式集一覧~
【ベクトル】1.ベクトルの演算
\(k, l\) は,実数とする。
① \(\vec{ a } + \vec{ b } = \vec{ b } + \vec{ a }\) , \( (\vec{ a } + \vec{ b }) + \vec{ c } = \vec{ a } + (\vec{ b } + \vec{ c })\)
② \(\vec{ a } + (- \vec{ a }) = \vec{ 0 }\) , \(\vec{ a } + \vec{ 0 } = \vec{ a }\), \(\vec{ a } – \vec{ b } = \vec{ a } + (-\vec{ b })\)
③ \((k + l) \vec{ a } = k \vec{ a } + l \vec{ a }\) , \( k(\vec{ a } + \vec{ b }) = k\vec{ a } + k\vec{ b }\)
④ \(\overrightarrow{ AB } + \overrightarrow{ BC } = \overrightarrow{ AC } \), \( \overrightarrow{ OA } – \overrightarrow{ OB } = \overrightarrow{ BA }\)
\(\overrightarrow{ AA } = \vec{ 0 }\), \(\overrightarrow{ BA } = -\overrightarrow{ AB }\)
【ベクトル】2.ベクトルの分解
\(\vec{ a } \neq \vec{ 0 }, \vec{ b } \neq 0\) で, \(\vec{ a }\), \(\vec{ b }\) が平行でないとき
① 平面上の任意のベクトル \(\vec{ p } = \color{red}{s \vec{ a } + t \vec{ b }}\) のただ1通りの形に表される。
② \( s \vec{ a } + t \vec{ b } = s’ \vec{ a } + t’ \vec{ b }\) \(\iff\) \(\color{red}{s = s’} \), \( \color{red}{t = t’}\)
\(\vec{ a } \neq \vec{ 0 }, \vec{ b } \neq 0, \vec{ c } \neq 0\) で, \(\vec{ a }\), \(\vec{ b }\) , \(\vec{ c }\) が同じ平面上にないとき
① 空間上の任意のベクトル \(\vec{ p } = \color{red}{s \vec{ a } + t \vec{ b } + + u \vec{ c }}\) のただ1通りの形に表される。
② \( s \vec{ a } + t \vec{ b } + u \vec{ c } = s’ \vec{ a } + t’ \vec{ b } + u’\vec{ c }\) \(\iff\) \(\color{red}{s = s’, t = t’, u = u’}\)
【ベクトル】3.ベクトルの成分
\( \vec{ a } = (a_1, a_2), \vec{ b } = (b_1, b_2)\) とする。
・相等:\( \vec{ a } = \vec{ b }\) \(\iff\) \(\color{red}{a_1 = b_1, a_2 = b_2}\)
・大きさ:\(\left| \vec{ a } \right| = \color{red}{\sqrt{a_1{}^2 + a_2{}^2}}\)
・成分による演算
\(k \vec{a} + l \vec{b} = k(a_1, a_2) + l(b_1 , b_2) = (ka_1 + lb_1 , ka_2 + lb_2)\)
※\(k, l\) は実数とする
\( \vec{ a } = (a_1, a_2, a_3), \vec{ b } = (b_1, b_2, b_3)\) とする。
・相等:\( \vec{ a } = \vec{ b }\) \(\iff\) \(\color{red}{a_1 = b_1, a_2 = b_2, , a_3 = b_3}\)
・大きさ:\(\left| \vec{ a } \right| = \color{red}{\sqrt{a_1{}^2 + a_2{}^2 + a_3{}^2}}\)
・成分による演算
\(k \vec{a} + l \vec{b} = k(a_1, a_2 , a_3) + l(b_1 , b_2 , b_3) = (ka_1 + lb_1 , ka_2 + lb_2 , ka_3 + lb_3)\)
※\(k, l\) は実数とする
【ベクトル】4.\(\overrightarrow{ AB }\) の成分と大きさ
\( \vec{ a } = (a_1, a_2), \vec{ b } = (b_1, b_2)\) とする。
\(\overrightarrow{ AB } = \color{red}{(b_1 – a_1, b_2 – a_2)}\)
\(\left|\overrightarrow{ AB }\right| = \color{red}{\sqrt{(b_1 – a_1)^2 + (b_2 – a_2)^2}}\)
\( \vec{ a } = (a_1, a_2, a_3), \vec{ b } = (b_1, b_2, b_3)\) とする。
\(\overrightarrow{ AB } = \color{red}{(b_1 – a_1, b_2 – a_2 , b_3 – a_3)}\)
\(\left|\overrightarrow{ AB }\right| = \color{red}{\sqrt{(b_1 – a_1)^2 + (b_2 – a_2)^2 + (b_3 – a_3)^2}}\)
【ベクトル】5.ベクトルの内積
\(\vec{a} \cdot \vec{b} = \color{red}{\left| \vec{a} \right| \left| \vec{b} \right| \cos\theta}\)
\((0^\circ \leq \theta \leq 180^\circ)\)
\(\cos\theta = \color{red}{\displaystyle\frac{\vec{a} \cdot \vec{b}}{\left| \vec{a} \right| \left| \vec{b} \right|}}\)
① \(\vec{ a } \cdot \vec{ b } = \vec{ b } \cdot \vec{ a }\)
② \(\begin{eqnarray}
\left\{
\begin{array}{l}
(\vec{a} + \vec{b}) \cdot \vec{c} = \vec{a} \cdot \vec{c} + \vec{b} \cdot \vec{c} \\
\vec{a} \cdot (\vec{b} + \vec{c}) = \vec{a} \cdot \vec{b} + \vec{a} \cdot \vec{c}
\end{array}
\right.
\end{eqnarray}\)
③ \((k \vec{a}) \cdot \vec{b} = \vec{a} \cdot (k\vec{b}) = k (\vec{a} \cdot \vec{b})\)
※\(k\) は実数
④ \(\vec{a} \cdot \vec{a} = \color{red}{\left| \vec{a} \right| {}^2}\)
⑤ \(\left| \vec{a} \right| = \color{red}{\sqrt{\vec{a} \cdot \vec{a}}}\)
【ベクトル】6.ベクトルの平行と垂直
\(\vec{a} \neq \vec{0}, \vec{b} \neq \vec{0}\) とする。
\(\vec{a} /\!/ \vec{b} \iff \color{red}{\vec{b} = k\vec{a}}\) (\(k\) は実数)
\(\vec{a} \perp \vec{b} \iff \color{red}{\vec{a} \cdot \vec{b} = 0}\)
【ベクトル】7.ベクトルの内積と成分
\(\vec{ a } \neq \vec{ 0 }\), \(\vec{ b } \neq \vec{ 0 }\), \(\vec{ a }, \vec{ b }\) のなす角 \(\theta\) \((0^\circ \leq \theta \leq 180^\circ )\) とする。
\(\vec{ a } = (a_1 , a_2), \vec{ b } = (b_1 , b_2)\) とする。
\(\vec{ a } \cdot \vec{ b } = \color{red}{a_1 b_1 + a_2 b_2}\)
\(\vec{ a } = (a_1 , a_2 , a_3), \vec{ b } = (b_1 , b_2 , b_3)\) とする。
\(\vec{ a } \cdot \vec{ b } = \color{red}{a_1 b_1 + a_2 b_2 + a_3 b_3}\)
【ベクトル】8.三角形の面積
\(△OAB\) において,
\(\overrightarrow{ OA } = \vec{ a } = (a_1 , a_2), \overrightarrow{ OB } = \vec{ b } = (b_1 , b_2)\) とすると,
面積 \(S = \color{red}{\displaystyle\frac{1}{2}\sqrt{\left| \vec{ a } \right|{}^2 \left| \vec{ b } \right|{}^2 – (\vec{ a } \cdot \vec{ b })^2} }\)\( \color{red}{= \displaystyle\frac{1}{2}\left| a_1 b_2 – a_2 b_1 \right|} \)
【ベクトル】9.位置ベクトル
\(A(\vec{ a }) ,B(\vec{ b }), C(\vec{ c })\) とする。
① \(\overrightarrow{ AB } = \color{red}{\vec{b} – \vec{a}}\)
② 線分\( AB\) を\(m : n\) に内分する点は \( \color{red}{\displaystyle\frac{n\vec{ a } + m\vec{ b }}{m + n}}\)
③ 線分 \(AB\) を\(m : n\) に外分する点は \( \color{red}{\displaystyle\frac{- n\vec{ a } + m\vec{ b }}{m – n}}\)
④ 線分 \(AB\) の中点は \( \color{red}{\displaystyle\frac{\vec{ a } + \vec{ b }}{2}}\)
④ 線分 \(AB\) の中点は \( \color{red}{\displaystyle\frac{\vec{ a } + \vec{ b } + \vec{ c }}{3}}\)
【ベクトル】10.ベクトル方程式
\((s, t)\) は実数とする。
点\(A(\vec{ a })\) を通り、\(\vec{ d } \) \((\vec{ d } \neq \vec{ 0 } )\) に平行な直線上のベクトル \(\vec{ p }\)は
\(\vec{ p } = \color{red}{\vec{ a } + t \vec{ d }}\)
※\(\vec{ d } \)を方向ベクトルという。
点\(P(\vec{ p })\) が2点\(A(\vec{ a })\), \(B(\vec{ b })\)を通る直線上にあるとき、
① \( \color{red}{\vec{ p } = (1 – t) \vec{ a } + t \vec{ b }}\)
② \( \color{red}{\vec{ p } = s \vec{ a } + t \vec{ b } ( s + t = 1)}\)
\(\overrightarrow{ OP } = s\overrightarrow{ OA } + t\overrightarrow{ OB }\) のとき,
① \(s + t = 1, s \geq 0 , t \geq 0 \) \(\iff\) 点 P の存在範囲は線分 AB 上
② \(0 \leq s + t \leq 1 , s \geq 0 , t \geq 0\) \(\iff\) 点 P の存在範囲は △OAB の周および内部
【ベクトル】11.ベクトルの表し方(まとめ)
\(k, s, t, u\) は実数とする。
① 点 \(P\) は直線 \(OA\)上にある ⇔ \(\color{red}{\overrightarrow{ OP } = k\overrightarrow{ OA }}\)
② 点\(P\) は直線 \(AB\) 上にある
\(\iff\) \(\color{red}{\overrightarrow{ OP } = s\overrightarrow{ OA } + t\overrightarrow{ OB } (s + t = 1)}\)
\(\iff\) \(\color{red}{\overrightarrow{ OP } = s\overrightarrow{ OA } + (1 – s)\overrightarrow{ OB }}\)
③ 点 \(P\)は平面 \(ABC\)上にある
\(\iff\) \(\color{red}{\overrightarrow{ OP } = s\overrightarrow{ OA } + t\overrightarrow{ OB } + u\overrightarrow{ OC } (s + t + u= 1)}\)
\(\iff\) \(\color{red}{\overrightarrow{ OP } = s\overrightarrow{ OA } + t\overrightarrow{ OB } + ( 1 – s -t)\overrightarrow{ OC }}\)
\(\iff\) \(\color{red}{\overrightarrow{ CP } = s\overrightarrow{ CA } + t\overrightarrow{ CB }}\)
【数学C】複素数平面~公式集一覧~
【複素数平面】1.共役な複素数の性質
\(z, \alpha, \beta\) は複素数, \(\alpha =a + bi\) とする。
① \(z\) が実数 ⇔ \(\color{red}{\overline{z} = z}\)
② \(z\) が純虚数 ⇔ \(\color{red}{\overline{z} = – z, z \neq 0}\)
① \(\color{red}{\alpha + \overline{\alpha} = 2a}\)
② \(\color{red}{\alpha \overline{\alpha} = a^2 + b^2}\)
③ \(\color{red}{\overline{\overline{\alpha}} = \alpha}\) ⇐共役な複素数のバーは2回で外れる
① \(\color{red}{\overline{\alpha + \beta} = \overline{\alpha} + \overline{\beta}}\)
② \(\color{red}{\overline{\alpha – \beta} = \overline{\alpha}}\) \(\color{red}{-}\) \(\color{red}{\overline{\beta}}\)
③ \(\color{red}{\overline{\alpha \beta} = \overline{\alpha}}\) \(\color{red}{\overline{\beta}}\)
特に、\(\color{red}{\overline{\alpha^n} = (\overline{\alpha})^n}\)
④ \(\color{red}{\overline{\left( \displaystyle\frac{\alpha}{\beta} \right)} = \displaystyle\frac{\overline{\alpha}}{\overline{\beta}}}\)
【複素数平面】2.複素数の絶対値(大きさ)
\(\alpha, z\)は複素数であり、 \(\alpha = a + bi\) とする
\(|\alpha| = |a + bi| = \color{red}{\sqrt{a^2 + b^2}}\)

① \(|\alpha| = |\overline{\alpha}| = |- \alpha|\)
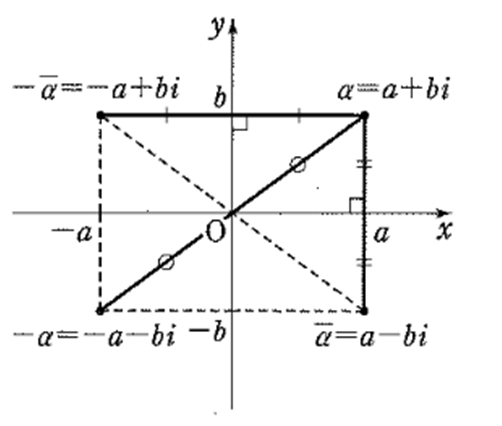
② \(\color{red}{z\overline{z} = |z|^2} \)
【複素数平面】3.複素数の演算と図示
\(\alpha, \beta\) は複素数とする。
\(\alpha = a + bi , \beta = c + di\) のとき
2点 \(\alpha , \beta\) 間の距離は \(|\beta – \alpha| = \color{red}{\sqrt{(c – a)^2 + (d – b)^2}}\)
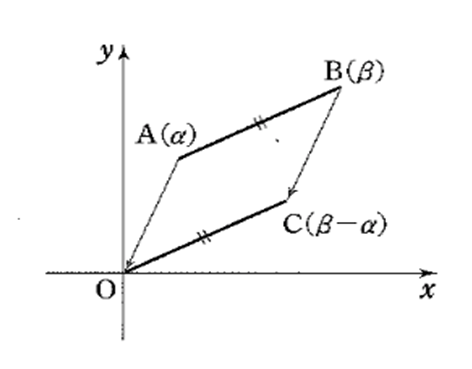
\(a \neq 0\) のとき
3点 \(0, \alpha, \beta\) が一直線上にある ⇔ \(\color{red}{\beta = k\alpha}\) となる実数 \(k\) がある
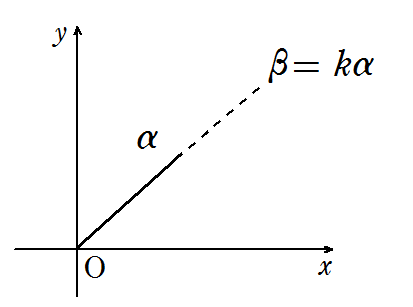
【複素数平面】4.複素数の極形式
\(\alpha, \beta, z\) は複素数とする。
\( \alpha = r_1 (\cos \theta_1 + i \sin \theta_1 ), \beta = r_2 (\cos \theta_2 + i \sin \theta_2 )\) のとき
① \(\color{red}{\alpha \beta = r_1 r_2 \{\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)\}}\)

② \(\color{red}{\displaystyle\frac{\alpha}{\beta} = \displaystyle\frac{r_1}{r_2}\{\cos(\theta_1 – \theta_2) + i\sin(\theta_1 – \theta_2) \}}\)
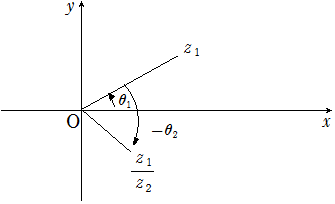
① \(\color{red}{|\alpha \beta| = |\alpha||\beta| , arg\alpha \beta = arg\alpha + arg\beta}\)
② \(\color{red}{\left|\displaystyle\frac{\alpha}{\beta}\right| = \displaystyle\frac{|\alpha|}{|\beta|} , arg\displaystyle\frac{\alpha}{\beta} = arg\alpha – arg\beta}\)
\(\alpha = \cos\theta + i\sin\theta\) と\(z\) に対して, 点 \(\alpha z\) は, 点 \(z\) を原点を中心として\(\theta\)だけ回転した点である。
【複素数平面】5.ド・モアブルの定理
\(n\) が整数のとき
\(\color{red}{(\cos\theta + i\sin\theta)^n = \cos n\theta + i\sin n\theta}\)
自然数 \(n\) に対して, \(1\) の\(n\) 乗根は,次の\(n\) 個の複素数になる
\(\color{red}{z_k = \cos\displaystyle\frac{2k\pi}{n} + i\sin\displaystyle\frac{2k\pi}{n}} \)
\((k = 0, 1, 2, \cdots, n – 1)\)
【複素数平面】6.複素数と図形
\(A(\alpha)\),\(B(\beta)\),\(C(\gamma)\) とする。
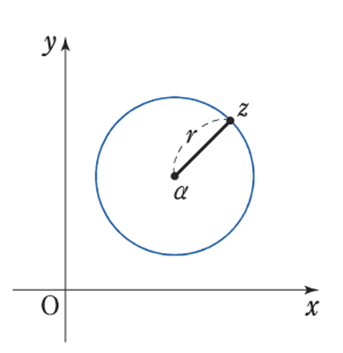
\(|z – \alpha| = \gamma \) ⇒ 点 A を中心とする半径\(r\) の円
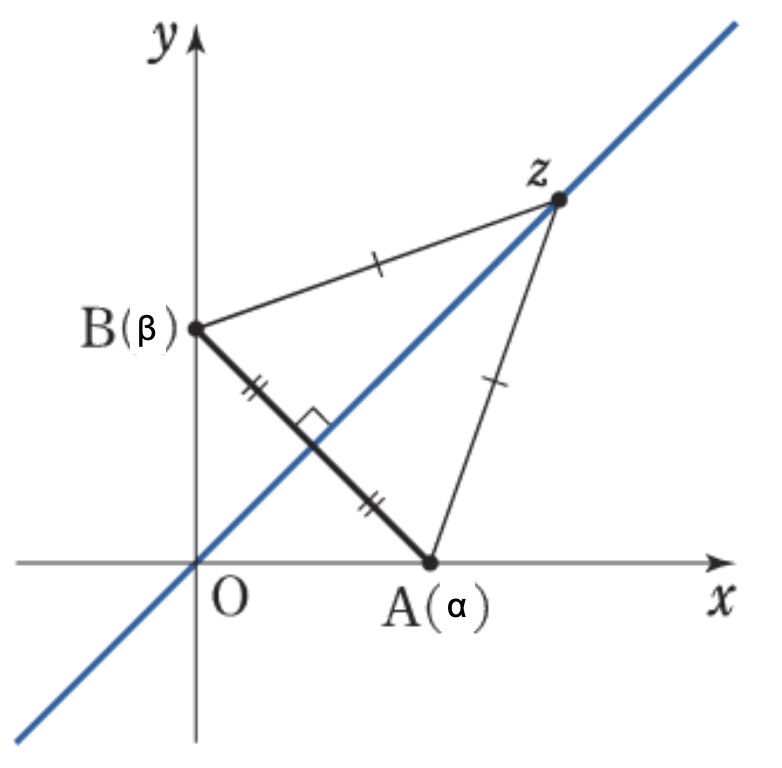
\(|z – \alpha| = |z – \beta| \) ⇒ 線分 AB の垂直二等分線
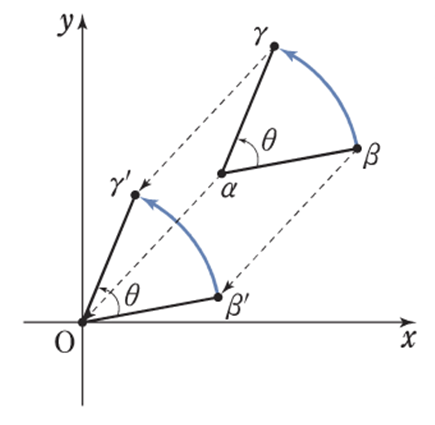
点 \(\beta\) を, 点\(\alpha\) を中心として角\(\theta\) だけ回転した点を\(\gamma\) とすると
\(\color{red}{\gamma – \alpha = (\cos\theta + i\sin\theta)(\beta – \alpha)}\)
\(A(\alpha), B(\beta), C(\gamma)\) について
半直線 AB から半直線 AC までの回転角\(\theta\) は
\(\color{red}{\theta = arg\displaystyle\frac{\gamma – \alpha}{\beta – \alpha}}\)
【数学C】式と曲線~公式集一覧~
【式と曲線】1.放物線
定点 \(F\) と\(F\) を通らない定直線 \(\ell\) からの距離が等しい点\(P\) の軌跡
※この定点\(F\) を焦点、定直線 \(\ell\)を準線という。
\(x\) 軸を軸とする放物線について
① 方程式は \(\color{red}{y^2 = 4px (p \neq 0)}\)
② 頂点は原点, 軸は\(x\) 軸
(曲線は軸に関して対称)
③ 焦点は\((\color{red}{F(p, 0)}\) , 準線は直線 \(\color{red}{x = -p}\)

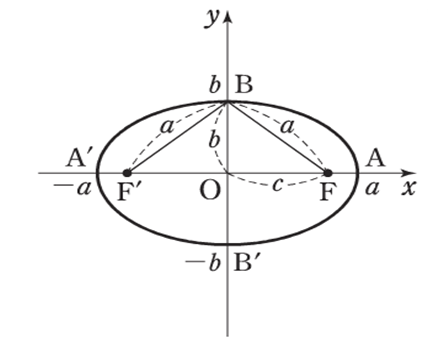
【式と曲線】2.楕円
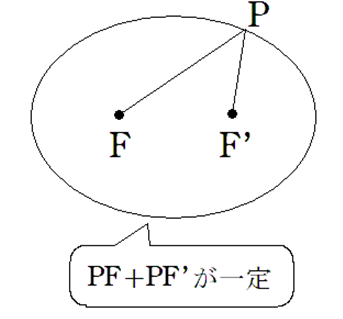
2定点\(F, F’\) からの距離の和が一定である点\(P\)の軌跡
(ただし、\(PF + PF’ > FF’\))
※2定点 \(F, F’\) を焦点という
長軸の長さ(AA’) が \(2a\), 短軸の長さ(BB’)が \(2b\) の楕円について
① 方程式は
\(\color{red}{\displaystyle\frac{x^2}{a^2} + \displaystyle\frac{y^2}{b^2} = 1}\)
② 焦点は
\(\color{red}{F(\sqrt{a^2 – b^2} , 0), F'(-\sqrt{a^2 – b^2} , 0)}\)
④ 頂点は
\((a, 0), (-a, 0), (0, b), (0, -b)\)
③ 楕円上の点から 2 つの焦点までの和は
\(\color{red}{2a}\)
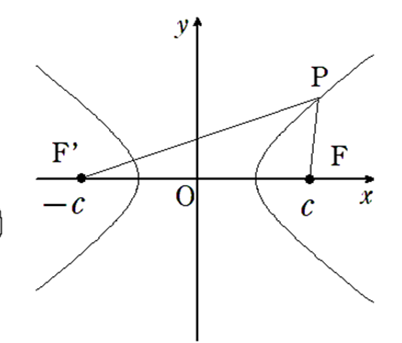
【式と曲線】3.双曲線
2定点\(F, F’\) からの距離の差が一定である点\(P\)の軌跡
※2定点 \(F, F’\) を焦点という
\(|PF – PF’|\)が一定
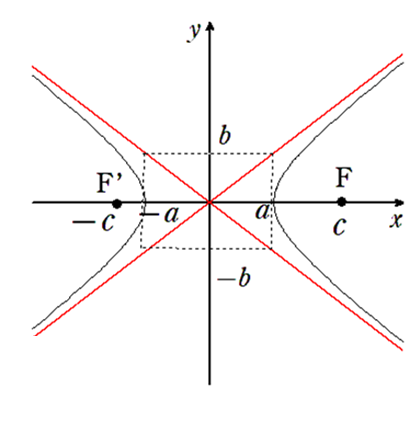
2定点 \(F(c, 0), F'(-c, 0)\) を焦点とし、定点からの距離の差が \(2a\) である双曲線について
① 方程式は
\(\color{red}{\displaystyle\frac{x^2}{a^2} – \displaystyle\frac{y^2}{b^2} = 1}\)
② 焦点は
\(\color{red}{F(\sqrt{a^2 + b^2} , 0), F'(-\sqrt{a^2 + b^2} , 0)}\)
※\(\color{red}{c = \sqrt{a^2 + b^2}}\)
③ 双曲線上の点から 2 つの焦点までの差は
\(\color{red}{2a}\)
④ 頂点は \((a, 0), (-a, 0)\)
⑤ 漸近線の方程式は
直線 \(\color{red}{y = \displaystyle\frac{b}{a}x, y = -\displaystyle\frac{b}{a}x}\)
【式と曲線】4.曲線の平行移動
曲線\(F(x, y) = 0\) を\(x\) 軸方向に\(p\), \(y\) 軸方向に\(q\) だけ平行移動して得られる曲線の方程式は
\(\color{red}{F(x – p, y – q) = 0}\) ←通常の平行移動と同じ
【式と曲線】5.2次曲線と直線の共有点
2次曲線と直線の方程式から1文字を消去して2次方程式が得られる場合,その2次方程式の実数解の個数と,2次曲線と直線の共有点の個数は一致する。
【式と曲線】6.2次曲線と接線
① 放物線\(y^2 =4px\) 上の点\((x_1 , y_1)\) における接線の方程式は
\(\color{red}{y_1y = 2p(x + x_1)}\)
② 楕円\(\displaystyle\frac{x^2}{a^2} + \displaystyle\frac{y^2}{b^2} = 1\)上の点\((x_1 , y_1)\) における接線の方程式は
\(\color{red}{\displaystyle\frac{x_1x}{a^2} + \displaystyle\frac{y_1y}{b^2} = 1}\)
③ 双曲線\(\displaystyle\frac{x^2}{a^2} – \displaystyle\frac{y^2}{b^2} = 1\)上の点\((x_1 , y_1)\) における接線の方程式は
\(\color{red}{\displaystyle\frac{x_1x}{a^2} – \displaystyle\frac{y_1y}{b^2} = 1}\)
【式と曲線】7.離心率と準線
定点\(F\) と, \(F\) を通らない定直線\(ell\) からの距離の比が \(e : 1\) である点の軌跡は
① \(0 < e < 1\) のとき \(F\) を焦点の1つとする楕円
② \(e = 1\) のとき \(F\) を焦点, \(\ell\) を準線とする放物線
③ \(e > 1\) のとき \(F\) を焦点の1つとする双曲線
※\(e\) を離心率という。
【式と曲線】8.曲線の媒介変数表示
① 放物線 \(y^2 = 4px\)
→ \(\color{red}{x = pt^2, y = 2pt}\)
② 円 \(x^2 + y^2 = a^2\)
→ \(\color{red}{x = a\cos\theta, y = a\sin\theta}\)
③ 楕円 \(\displaystyle\frac{x^2}{a^2} + \displaystyle\frac{y^2}{b^2} = 1\)
→ \(\color{red}{x = a\cos\theta, y = b\sin\theta}\)
④ 双曲線 \(\displaystyle\frac{x^2}{a^2} – \displaystyle\frac{y^2}{b^2} = 1\)
→ \(\color{red}{x = \displaystyle\frac{a}{\cos\theta}, y = b\tan\theta}\)
⑤ サイクロイド
→ \(x = a(\theta – \sin\theta), y = a(1 – \cos\theta)\)
※\(p \neq 0 , a > 0, b > 0\)
曲線 \(x = f(t), y = g(t)\) を,\(x\)軸方向に\(p\) ,\(y\)軸方向に\(q\) だけ平行移動した曲線は
\(\color{red}{x = f(t) + p , y = g(t) + q} \)
【式と曲線】9.極座標と極方程式
① \(\color{red}{x = r\cos\theta , y = r\sin\theta}\)
② \(\color{red}{r = \sqrt{x^2 + y^2}}\)
\(r \neq 0\) のとき \(\cos\theta = \displaystyle\frac{x}{r}, \sin\theta = \displaystyle\frac{y}{r}\)
① 中心が極\(O\), 半径が\(a\) の円の極方程式は
\(\color{red}{r = a}\)
② 中心の極座標が\((a, 0)\), 半径が\(a\) の円の極方程式は
\(\color{red}{r = 2a\cos\theta}\)
③ 中心の極座標が\((r_1, \theta_1)\), 半径が\(a\)の円の極方程式は
\(\color{red}{r^2 + r_1{}^2 – 2rr_1 \cos(\theta – \theta_1) = a^2}\)
① 極\(O\) を通り, 始線とのなす角が\(\alpha\) である直線の極方程式は
\(\color{red}{\theta = \alpha}\)
② \(A(r_1, \theta_1)\) を通り, OA に垂直な直線の極方程式は
\(\color{red}{r\cos(\theta – \theta_1) = r_1}\)
※\(r_1 > 0\)
極座標が\((a, 0)\) である点を通り,始線 OX に垂直な直線を\(\ell\) とすると、次の極方程式は2次曲線を表す。
\(r = \displaystyle\frac{ea}{1 + e\cos\theta}\)
① \(0 < e < 1\) のとき \(O\) を焦点の1つとする楕円
② \(e = 1\) のとき \(O\) を焦点, \(\ell\) を準線とする放物線
③ \(e > 1\) のとき \(O\) を焦点の1つとする双曲線
【数学C】数学的な表現の工夫~公式集一覧~
【数学的な表現の工夫】1.データの表現方法の工夫
【数学的な表現の工夫】2.行列による表現
以下のように,いくつかの数や文字を長方形状に書き並べ,両端を括弧で囲んだものを行列といい,括弧の中のそれぞれの数や文字を,この行列の成分という。
また,\(m\) 個の行と\(n\) 個の列からなる行列を\(m\) 行 \(n\) 列の行列、または、\(m \times n\) 行列といい,特に,行と列の個数が等しい\(n \times n\) 行列を,\(n\)次の正方行列という。
\(\begin{eqnarray}
\left(
\begin{array}{ccc}
3 & 2 & 5 \\
4 & 3 & 2 \\
1 & 5 & 3 \\
\end{array}
\right)
\end{eqnarray}\)
2つの行列\(A, B\) が行数と列数がともに等しいとき,\(A\) と \(B\) は同じ型であるという。
\(A, B\)が同じ型であり,かつ対応する成分がそれぞれ等しいとき,\(A\) と \(B\) は等しいといい\(A = B\)で表す。
また、行列\(A, B\)が同じ型であるとき,
\(A, B\) の対応する成分の和を成分とする行列を\(A, B\)の和といい,\(A + B\) で表す。
\(A, B\) の対応する成分の差を成分とする行列を\(A, B\)の差といい,\(A – B\) で表す。
成分がすべて\(0\) である行列を零行列といい,記号\(O\) で表す。
2つの行列\(A, B\),および零行列 \(O\) について次の計算法則が成り立つ。
① \(A + B = B + A\) (交換法則)
② \((A + B) + C = A + (B + C)\) (結合法則)
③ \(A – A = O, A + O = A \)
\(k\) を実数とするとき,行列\(A\) の各成分の \(k\) 倍を成分とする行列を\(\color{red}{kA}\) で表す。
2つの行列\(A, B\),および実数 \(k, l\) について次の計算法則が成り立つ。
① \(k(lA) = (kl)A \)
② \((k + l)A = kA + lA\)
③ \(k(A + B) = kA + kB\)
\(1 \times m\) 行列 を \(m\) 次の行ベクトル,\(n \times 1\) 行列 を \(n\) 次の列ベクトルという。
\(m\) 次の行ベクトル \(A\), \(m\) 次の列ベクトル\(B\) について,その対応する成分の積の和を,積\(AB\)と定める。
すなわち,
\(A = \begin{eqnarray}
\left(
\begin{array}{cccc}
a_1 & a_2 & \cdots & a_m\\
\end{array}
\right)
\end{eqnarray}\) , \(B = \begin{eqnarray}
\left(
\begin{array}{cccc}
b_1\\
b_2\\
\vdots\\
b_m\\
\end{array}
\right)
\end{eqnarray}\) に対して,
積\(AB = \begin{eqnarray}
\left(
\begin{array}{cccc}
a_1 & a_2 & \cdots & a_m\\
\end{array}
\right)
\end{eqnarray}\) \(\begin{eqnarray}
\left(
\begin{array}{cccc}
b_1\\
b_2\\
\vdots\\
b_m\\
\end{array}
\right)
\end{eqnarray}\)
\(= a_1b_1 + a_2b_2 + \cdots\cdots + a_mb_m\)
で定める。
一般に,\(m \times n\) 行列 \(A\), \(n \times l\) 行列\(B\) について,積\(AB\)は\(m \times l\) 行列となり,以下の計算規則が成り立つ。
\(\begin{eqnarray}
\left(
\begin{array}{cccc}
a_{11} & a_{12} &\cdots & a_{1n}\\
a_{21} & a_{22} &\cdots & a_{2n}\\
\vdots & \vdots &\ddots & \vdots\\
a_{m1} & a_{m2} &\cdots & a_{mn}\\
\end{array}
\right)
\end{eqnarray}\)\(\begin{eqnarray}
\left(
\begin{array}{cccc}
b_{11} & b_{12} &\cdots & b_{1l}\\
b_{21} & b_{22} &\cdots & b_{2l}\\
\vdots & \vdots &\ddots & \vdots\\
b_{n1} & b_{n2} &\cdots & b_{nl}\\
\end{array}
\right)
\end{eqnarray}\)
\(= \begin{eqnarray}
\left(
\begin{array}{cccc}
\displaystyle\sum_{k=1}^{n}a_{1k}b_{k1} & \displaystyle\sum_{k=1}^{n}a_{1k}b_{k2} &\cdots & \displaystyle\sum_{k=1}^{n}a_{1k}b_{kl}\\
\displaystyle\sum_{k=1}^{n}a_{2k}b_{k1} & \displaystyle\sum_{k=1}^{n}a_{2k}b_{k2} &\cdots & \displaystyle\sum_{k=1}^{n}a_{2k}b_{kl}\\
\vdots & \vdots &\ddots & \vdots\\
\displaystyle\sum_{k=1}^{n}a_{mk}b_{k1} & \displaystyle\sum_{k=1}^{n}a_{mk}b_{k2} &\cdots & \displaystyle\sum_{k=1}^{n}a_{mk}b_{kl}\\
\end{array}
\right)
\end{eqnarray}\)
※ただし,\(A\) の列数と\(B\) の行数が異なるときは,積\(AB\) は考えない。
2つの行列\(A, B\),および実数 \(k\) について次の計算法則が成り立つ。
① \((kA)B = A(kB) = k(AB)\)
② \((AB)C = A(BC)\) (結合法則)
③ \((A + B) C = AC + BC , A (B + C) = AB + AC\) (分配法則)
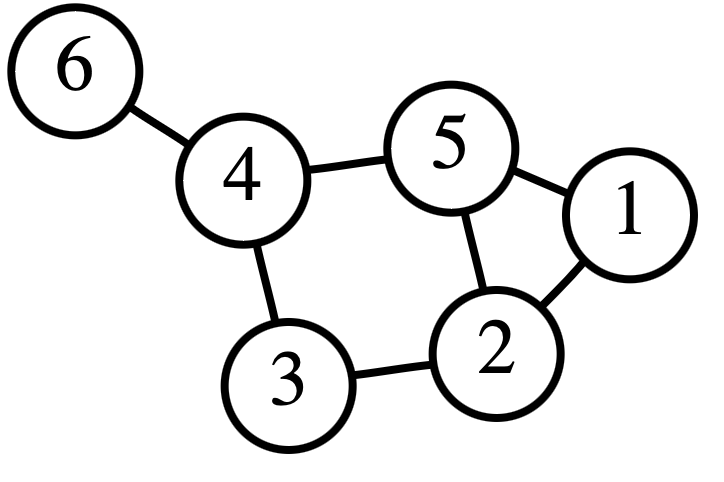
【数学的な表現の工夫】3.離散グラフによる表現
【数学的な表現の工夫】4.離散グラフと行列の関連
離散グラフの頂点を\(P_1, P_2, \cdots\cdots, P_n\) とするとき,\(n\) 次の正方行列\(A\) の\((i, j)\) 成分を,2つの頂点\(P_i, P_j\) を結ぶ辺の本数とするように定めた行列\(A\) を離散グラフの隣接行列という。







コメント