【数学C】数学的な表現の工夫〜基本公式・例題一覧〜

データを項目別に大きい順に並び替えたグラフに項目の累積度数の全体に対する割合を表す折れ線グラフを重ねた図をパレート図という。グラフの右側の縦軸の目盛りは，累積度数の全体に対する割合（%）を表しており，累積比率という。
※パレート図は，問題を重点化し，効率的かつ効果的に目標を達成するために用いられる。

ある３つの変量を横軸，縦軸，円の大きさで１つの図で表したものをバブルチャートという。
※バブルチャートは，３つの変量を視覚的に捉えることができる点で優れている。

以下のように，いくつかの数や文字を長方形状に書き並べ，両端を括弧で囲んだものを行列といい，括弧の中のそれぞれの数や文字を，この行列の成分という。
また，\(m\) 個の行と\(n\) 個の列からなる行列を\(m\) 行 \(n\) 列の行列、または、\(m \times n\) 行列といい，特に，行と列の個数が等しい\(n \times n\) 行列を，\(n\)次の正方行列という。

\(\begin{eqnarray}
\left(
\begin{array}{ccc}
3 & 2 & 5 \\
4 & 3 & 2 \\
1 & 5 & 3 \\
\end{array}
\right)
\end{eqnarray}\)

２つの行列\(A, B\) が行数と列数がともに等しいとき，\(A\) と \(B\) は同じ型であるという。
\(A, B\)が同じ型であり，かつ対応する成分がそれぞれ等しいとき，\(A\) と \(B\) は等しいといい\(A = B\)で表す。

また、行列\(A, B\)が同じ型であるとき，

\(A, B\) の対応する成分の和を成分とする行列を\(A, B\)の和といい，\(A + B\) で表す。

\(A, B\) の対応する成分の差を成分とする行列を\(A, B\)の差といい，\(A – B\) で表す。

成分がすべて\(0\) である行列を零行列といい，記号\(O\) で表す。

２つの行列\(A, B\)，および零行列 \(O\) について次の計算法則が成り立つ。

① \(A + B = B + A\) （交換法則）

② \((A + B) + C = A + (B + C)\)　（結合法則）

③ \(A – A = O, A + O = A \)

\(k\) を実数とするとき，行列\(A\) の各成分の \(k\) 倍を成分とする行列を\(\color{red}{kA}\) で表す。

２つの行列\(A, B\)，および実数 \(k, l\) について次の計算法則が成り立つ。

① \(k(lA) = (kl)A \)

② \((k + l)A = kA + lA\)

③ \(k(A + B) = kA + kB\)

\(1 \times m\) 行列 を \(m\) 次の行ベクトル，\(n \times 1\) 行列 を \(n\) 次の列ベクトルという。
\(m\) 次の行ベクトル \(A\)， \(m\) 次の列ベクトル\(B\) について，その対応する成分の積の和を，積\(AB\)と定める。

すなわち，

\(A = \begin{eqnarray}
\left(
\begin{array}{cccc}
a_1 & a_2 & \cdots & a_m\\
\end{array}
\right)
\end{eqnarray}\) , \(B = \begin{eqnarray}
\left(
\begin{array}{cccc}
b_1\\
b_2\\
\vdots\\
b_m\\
\end{array}
\right)
\end{eqnarray}\)　に対して，

積\(AB = \begin{eqnarray}
\left(
\begin{array}{cccc}
a_1 & a_2 & \cdots & a_m\\
\end{array}
\right)
\end{eqnarray}\) \(\begin{eqnarray}
\left(
\begin{array}{cccc}
b_1\\
b_2\\
\vdots\\
b_m\\
\end{array}
\right)
\end{eqnarray}\)

\(= a_1b_1 + a_2b_2 + \cdots\cdots + a_mb_m\)

で定める。

一般に，\(m \times n\) 行列 \(A\)， \(n \times l\) 行列\(B\) について，積\(AB\)は\(m \times l\) 行列となり，以下の計算規則が成り立つ。

\(\begin{eqnarray}
\left(
\begin{array}{cccc}
a_{11} & a_{12} &\cdots & a_{1n}\\
a_{21} & a_{22} &\cdots & a_{2n}\\
\vdots & \vdots &\ddots & \vdots\\
a_{m1} & a_{m2} &\cdots & a_{mn}\\
\end{array}
\right)
\end{eqnarray}\)\(\begin{eqnarray}
\left(
\begin{array}{cccc}
b_{11} & b_{12} &\cdots & b_{1l}\\
b_{21} & b_{22} &\cdots & b_{2l}\\
\vdots & \vdots &\ddots & \vdots\\
b_{n1} & b_{n2} &\cdots & b_{nl}\\
\end{array}
\right)
\end{eqnarray}\)

\(= \begin{eqnarray}
\left(
\begin{array}{cccc}
\displaystyle\sum_{k=1}^{n}a_{1k}b_{k1} & \displaystyle\sum_{k=1}^{n}a_{1k}b_{k2} &\cdots & \displaystyle\sum_{k=1}^{n}a_{1k}b_{kl}\\
\displaystyle\sum_{k=1}^{n}a_{2k}b_{k1} & \displaystyle\sum_{k=1}^{n}a_{2k}b_{k2} &\cdots & \displaystyle\sum_{k=1}^{n}a_{2k}b_{kl}\\
\vdots & \vdots &\ddots & \vdots\\
\displaystyle\sum_{k=1}^{n}a_{mk}b_{k1} & \displaystyle\sum_{k=1}^{n}a_{mk}b_{k2} &\cdots & \displaystyle\sum_{k=1}^{n}a_{mk}b_{kl}\\
\end{array}
\right)
\end{eqnarray}\)

※ただし，\(A\) の列数と\(B\) の行数が異なるときは，積\(AB\) は考えない。

２つの行列\(A, B\)，および実数 \(k\) について次の計算法則が成り立つ。

① \((kA)B = A(kB) = k(AB)\)

② \((AB)C = A(BC)\) （結合法則）

③ \((A + B) C = AC + BC , A (B + C) = AB + AC\)　（分配法則）

いくつかの点とそれらを結ぶ何本かの線で表された図を離散グラフという。

離散グラフのどの２頂点も，いくつかの辺をたどって一方から他方に行けるとき，離散グラフは連結であるという。

離散グラフの頂点を\(P_1, P_2, \cdots\cdots, P_n\) とするとき，\(n\) 次の正方行列\(A\) の\((i, j)\) 成分を，２つの頂点\(P_i, P_j\) を結ぶ辺の本数とするように定めた行列\(A\) を離散グラフの隣接行列という。

例題

以下の離散グラフの隣接行列を求めよ。

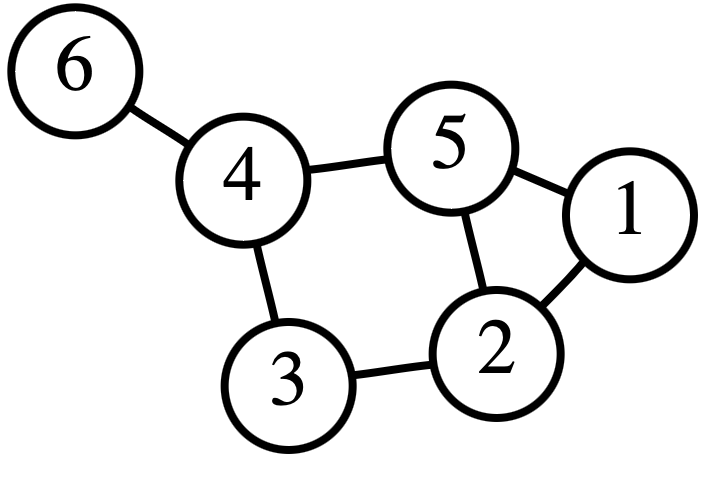
解答

例えば①と以下の①〜⑥を結ぶ辺の本数は以下のようになる。

① … ０本　，② … １本　，③ … ０本　，④ … ０本　，⑤ … １本　，⑥ … ０本

②〜⑥においても上記と同様に辺の本数を求め行列にすると以下になる。

\(\begin{eqnarray}
\left(
\begin{array}{cccccc}
0 & 1 & 0 & 0 & 1 & 0\\
1 & 0 & 1 & 0 & 1 & 0\\
0 & 1 & 0 & 1 & 0 & 0\\
0 & 0 & 1 & 0 & 1 & 1\\
1 & 1 & 0 & 1 & 0 & 0\\
0 & 0 & 0 & 1 & 0 & 0\\
\end{array}
\right)
\end{eqnarray}\)\(\begin{eqnarray}