このページは【図形と計量(三角比)】の問題まとめページです。
特に重要な基礎問題と解答を単元別に一問一答式で出題しています。
問題解き、解説をしっかり読んで理解することで、定着を図ることができます。
【図形と計量(三角比)】基本問題一覧〜一問一答式(高校数学I)〜
三角比の定義・相互関係
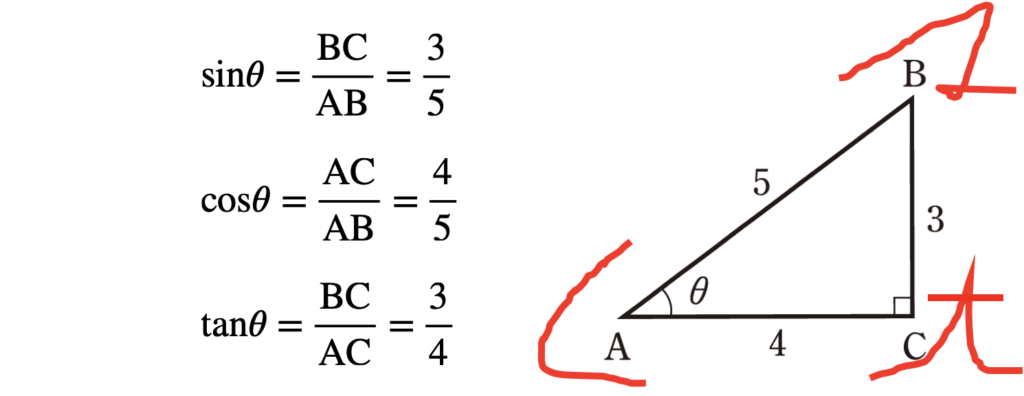
次の直角三角形において,\(\sin\theta , \cos\theta, \tan\theta\) の値を求めよ。
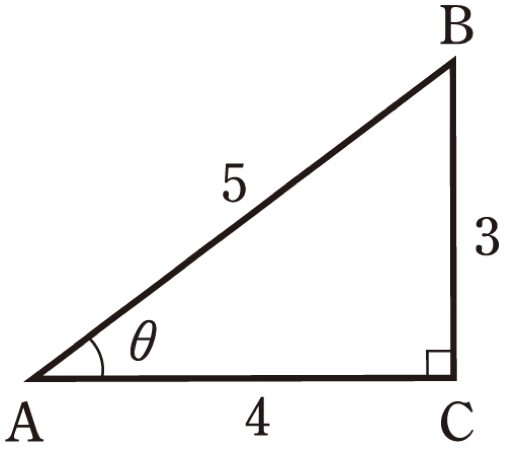
解答・解説
直角三角形ABCで、∠C=90°, AB=13, BC=5 のとき、辺ACの長さを求め、sinB, cosB, tanB の値を求めなさい。
解答・解説
まず、三平方の定理 a² + b² = c² を使って、辺ACの長さを求めます。 AC² + BC² = AB² AC² + 5² = 13² AC² + 25 = 169 AC² = 144 AC = 12 (長さなので正の数)
次に、角Bに着目して三角比を求めます。
- 高さ (角Bの対辺) = AC = 12
- 底辺 (角Bの隣辺) = BC = 5
- 斜辺 = AB = 13
よって、
- sinB = 高さ / 斜辺 = AC / AB = 12/13
- cosB = 底辺 / 斜辺 = BC / AB = 5/13
- tanB = 高さ / 底辺 = AC / BC = 12/5
0° < θ < 90° で、sinθ = 2/3 のとき、cosθ と tanθ の値を求めなさい。
解答・解説
三角比の相互関係の公式 sin²θ + cos²θ = 1 を使います。 (2/3)² + cos²θ = 1 4/9 + cos²θ = 1 cos²θ = 1 – 4/9 = 5/9 0° < θ < 90° のとき、cosθ は正の数なので、 cosθ = √(5/9) = (√5)/3
次に、公式 tanθ = sinθ / cosθ を使います。 tanθ = (2/3) / ((√5)/3) = 2/3 × 3/√5 = 2/√5 分母を有理化して、tanθ = (2√5)/5
0° < θ < 90° で、tanθ = 2 のとき、sinθ と cosθ の値を求めなさい
解答・解説
三角比の相互関係の公式 1 + tan²θ = 1/cos²θ を使います。 1 + 2² = 1/cos²θ 1 + 4 = 1/cos²θ 5 = 1/cos²θ cos²θ = 1/5 0° < θ < 90° のとき、cosθ は正の数なので、 cosθ = √(1/5) = 1/√5 = (√5)/5
次に、公式 sinθ = tanθ × cosθ を使います。 sinθ = 2 × (1/√5) = 2/√5 = (2√5)/5
次の値を求めなさい。 (1) sin30° (2) cos45° (3) tan60°
解答・解説
30°, 45°, 60°の三角比は、特別な直角三角形の辺の比から導かれます。これらは必ず覚えましょう。
(1) sin30° = 1/2 (2) cos45° = 1/√2 (または √2/2) (3) tan60° = √3
直角三角形ABCで、∠C=90°, ∠B=30°, AB=8 のとき、辺ACと辺BCの長さを求めなさい。
解答・解説
三角比の定義を利用して辺の長さを計算します。
AC = AB × sinBBC = AB × cosB
(辺ACの長さ) AC = 8 × sin30° sin30° = 1/2 なので、 AC = 8 × (1/2) = 4
(辺BCの長さ) BC = 8 × cos30° cos30° = √3/2 なので、 BC = 8 × (√3/2) = 4√3
AC=6, BC=x, AB=y, ∠A=60°, ∠C=90°である直角三角形で、x と y の値を求めなさい。
解答・解説
(xの値を求める) tanA = BC / AC なので x = AC × tanA x = 6 × tan60° tan60° = √3 なので、 x = 6√3
(yの値を求める) cosA = AC / AB なので y = AC / cosA y = 6 / cos60° cos60° = 1/2 なので、 y = 6 / (1/2) = 6 × 2 = 12
直角三角形ABCで、AB=6, AC=3 のとき、∠Aの大きさを求めなさい。(∠C=90°とする)
解答・解説
分かっている辺は、斜辺(AB)と、角Aの隣辺(AC)です。 この2つの辺の関係は cos で表せます。 cosA = 隣辺 / 斜辺 = AC / AB cosA = 3 / 6 = 1/2 cosA = 1/2 となる角度Aは 60° です。
直角三角形ABCで、AC=7, BC=7 のとき、∠Aの大きさを求めなさい。(∠C=90°とする)
解答・解説
分かっている辺は、角Aの対辺(BC)と、角Aの隣辺(AC)です。 この2つの辺の関係は tan で表せます。 tanA = 対辺 / 隣辺 = BC / AC tanA = 7 / 7 = 1 tanA = 1 となる角度Aは 45° です。
木の根元から水平に12m離れた地点Pに立ち、木のてっぺんAを見上げた角度(∠APB)が30°でした。目の高さを1.6mとすると、木の高さは何mですか。小数第2位を四捨五入して答えなさい。
解答・解説
まず、目の高さから上の部分の木の高さを求めます。この高さを hとします。 地点Pから木までの水平距離は12mです。 tan30° = 高さ / 底辺 = h / 12 という関係が成り立ちます。 h = 12 × tan30° tan30° = 1/√3なので、 h = 12 / √3 = 4√3
√3 ≒ 1.732 なので、 h ≒ 4 × 1.732 = 6.928 m
木の全体の高さは、この h に目の高さ 1.6m を加えたものです。 木の高さ = 6.928 + 1.6 = 8.528 m
小数第2位を四捨五入すると、答えは 8.5m となります。
三角比の拡張
\(\sin 120^\circ\) の値を求めなさい。
解答・解説
\(120^\circ\) は \(180^\circ – 60^\circ\) と考えることができます。
三角比の公式 \(\sin(180^\circ – \theta) = \sin\theta\) を使います。
この公式で \(\theta = 60^\circ\) とすると、
\(\sin 120^\circ = \sin(180^\circ – 60^\circ) = \sin 60^\circ\)
よって、\(\sin 120^\circ = \frac{\sqrt{3}}{2}\) となります。
\(\cos 135^\circ\) の値を求めなさい。
解答・解説
\(135^\circ\) は \(180^\circ – 45^\circ\) と考えることができます。
三角比の公式 \(\cos(180^\circ – \theta) = -\cos\theta\) を使います。
この公式で \(\theta = 45^\circ\) とすると、
\(\cos 135^\circ = \cos(180^\circ – 45^\circ) = -\cos 45^\circ\)
よって、\(\cos 135^\circ = -\frac{1}{\sqrt{2}}\) (または \(-\frac{\sqrt{2}}{2}\))となります。
\(\tan 150^\circ\) の値を求めなさい。
解答・解説
\(150^\circ\) は \(180^\circ – 30^\circ\) と考えることができます。
三角比の公式 \(\tan(180^\circ – \theta) = -\tan\theta\) を使います。
この公式で \(\theta = 30^\circ\) とすると、
\(\tan 150^\circ = \tan(180^\circ – 30^\circ) = -\tan 30^\circ\)
よって、\(\tan 150^\circ = -\frac{1}{\sqrt{3}}\) (または \(-\frac{\sqrt{3}}{3}\))となります。
\(0^\circ \le \theta \le 180^\circ\) のとき、\(\sin\theta = \frac{4}{5}\) を満たす \(\cos\theta\) と \(\tan\theta\) の値を求めなさい。
解答・解説
三角比の相互関係の公式 \(\sin^2\theta + \cos^2\theta = 1\) を使います。
\(\sin\theta = \frac{4}{5}\) を代入すると、
\((\frac{4}{5})^2 + \cos^2\theta = 1\)
\(\frac{16}{25} + \cos^2\theta = 1\)
\(\cos^2\theta = 1 – \frac{16}{25} = \frac{9}{25}\)
\(\cos\theta = \pm\sqrt{\frac{9}{25}} = \pm\frac{3}{5}\)
ここで、\(0^\circ \le \theta \le 180^\circ\) の範囲を考えます。
(i) \(\theta\) が鋭角 (\(0^\circ < \theta < 90^\circ\)) の場合
\(\cos\theta > 0\) なので、\(\cos\theta = \frac{3}{5}\)
このとき、\(\tan\theta = \frac{\sin\theta}{\cos\theta} = \frac{4/5}{3/5} = \frac{4}{3}\)
(ii) \(\theta\) が鈍角 (\(90^\circ < \theta < 180^\circ\)) の場合
\(\cos\theta < 0\) なので、\(\cos\theta = -\frac{3}{5}\)
このとき、\(\tan\theta = \frac{\sin\theta}{\cos\theta} = \frac{4/5}{-3/5} = -\frac{4}{3}\)
よって、答えは
\(\cos\theta = \frac{3}{5}, \tan\theta = \frac{4}{3}\) または \(\cos\theta = -\frac{3}{5}, \tan\theta = -\frac{4}{3}\) の2組です。
\(90^\circ < \theta < 180^\circ\) のとき、\(\cos\theta = -\frac{12}{13}\) を満たす \(\sin\theta\) と \(\tan\theta\) の値を求めなさい。
解答・解説
公式 \(\sin^2\theta + \cos^2\theta = 1\) を使います。
\(\cos\theta = -\frac{12}{13}\) を代入すると、
\(\sin^2\theta + (-\frac{12}{13})^2 = 1\)
\(\sin^2\theta + \frac{144}{169} = 1\)
\(\sin^2\theta = 1 – \frac{144}{169} = \frac{25}{169}\)
\(\sin\theta = \pm\sqrt{\frac{25}{169}} = \pm\frac{5}{13}\)
問題の条件で \(90^\circ < \theta < 180^\circ\) なので、\(\sin\theta > 0\) です。
よって、\(\sin\theta = \frac{5}{13}\)
次に \(\tan\theta\) を求めます。公式 \(\tan\theta = \frac{\sin\theta}{\cos\theta}\) を使います。
\(\tan\theta = \frac{5/13}{-12/13} = -\frac{5}{12}\)
答え:\(\sin\theta = \frac{5}{13}, \tan\theta = -\frac{5}{12}\)
\(0^\circ \le \theta \le 180^\circ\) のとき、\(\tan\theta = -3\) を満たす \(\sin\theta\) と \(\cos\theta\) の値を求めなさい。
解答・解説
公式 \(1 + \tan^2\theta = \frac{1}{\cos^2\theta}\) を使います。
\(\tan\theta = -3\) を代入すると、
\(1 + (-3)^2 = \frac{1}{\cos^2\theta}\)
\(1 + 9 = \frac{1}{\cos^2\theta}\)
\(10 = \frac{1}{\cos^2\theta}\)
\(\cos^2\theta = \frac{1}{10}\)
\(\cos\theta = \pm\sqrt{\frac{1}{10}} = \pm\frac{1}{\sqrt{10}}\)
\(\tan\theta = -3\) は負の値なので、\(\theta\) は鈍角 (\(90^\circ < \theta < 180^\circ\)) です。
鈍角のとき \(\cos\theta < 0\) なので、\(\cos\theta = -\frac{1}{\sqrt{10}}\)
次に \(\sin\theta\) を求めます。公式 \(\tan\theta = \frac{\sin\theta}{\cos\theta}\) を変形して \(\sin\theta = \tan\theta \times \cos\theta\) とします。
\(\sin\theta = (-3) \times (-\frac{1}{\sqrt{10}}) = \frac{3}{\sqrt{10}}\)
答え:\(\sin\theta = \frac{3}{\sqrt{10}}, \cos\theta = -\frac{1}{\sqrt{10}}\) (有理化して \(\sin\theta = \frac{3\sqrt{10}}{10}, \cos\theta = -\frac{\sqrt{10}}{10}\) でもよい)
\(\sin 20^\circ + \sin 70^\circ + \cos 110^\circ + \cos 160^\circ$ \) の値を求めなさい。
解答・解説
\(180^\circ – \theta\) の公式を使って、角度を鋭角にそろえます。
\(\cos 110^\circ = \cos(180^\circ – 70^\circ) = -\cos 70^\circ\)
\(\cos 160^\circ = \cos(180^\circ – 20^\circ) = -\cos 20^\circ\)
さらに、\(90^\circ – \theta\) の公式 \(\cos(90^\circ – \theta) = \sin\theta\)、\(\sin(90^\circ – \theta) = \cos\theta\) を使います。
\(\sin 70^\circ = \sin(90^\circ – 20^\circ) = \cos 20^\circ\)
\(\cos 70^\circ = \cos(90^\circ – 20^\circ) = \sin 20^\circ\)
これらを元の式に代入します。
元の式 =\(\sin 20^\circ + \sin 70^\circ + \cos 110^\circ + \cos 160^\circ\)
\(= \sin 20^\circ + \cos 20^\circ – \cos 70^\circ – \cos 20^\circ\)
\(= \sin 20^\circ + \cos 20^\circ – \sin 20^\circ – \cos 20^\circ = 0\)
答え:\(0\)
直線 \(y = -\sqrt{3}x + 1\) と \(x\) 軸の正の向きとのなす角 \(\theta\) (\(0^\circ \le \theta \le 180^\circ\)) を求めなさい。
解答・解説
直線の傾きは \(\tan\theta\) と等しくなります。
この直線の傾きは \(-\sqrt{3}\) です。
よって、\(\tan\theta = -\sqrt{3}\) となります。
\(\tan\theta\) が負の値なので、\(\theta\) は鈍角です。
まず、\(\tan\alpha = \sqrt{3}\) となる鋭角 \(\alpha\) を考えます。
\(\alpha = 60^\circ\) です。
公式 \(\tan(180^\circ – \alpha) = -\tan\alpha\) を使うと、
\(\tan(180^\circ – 60^\circ) = -\tan 60^\circ = -\sqrt{3}\)
したがって、\(\theta = 180^\circ – 60^\circ = 120^\circ\) です。
答え:\(\theta = 120^\circ\)
\(\tan 120^\circ \sin 120^\circ + \cos 150^\circ \tan 150^\circ\) の値を計算しなさい。
解答・解説
それぞれの三角比の値を求めます。
\(\tan 120^\circ = -\tan 60^\circ = -\sqrt{3}\)
\(\sin 120^\circ = \sin 60^\circ = \frac{\sqrt{3}}{2}\)
\(\cos 150^\circ = -\cos 30^\circ = -\frac{\sqrt{3}}{2}\)
\(\tan 150^\circ = -\tan 30^\circ = -\frac{1}{\sqrt{3}}\)
これらの値を元の式に代入します。
式 = \((-\sqrt{3}) \times (\frac{\sqrt{3}}{2}) + (-\frac{\sqrt{3}}{2}) \times (-\frac{1}{\sqrt{3}})\)
= \(-\frac{3}{2} + \frac{1}{2}\)
= \(-\frac{2}{2}\)
= \(-1\)
答え:\(-1\)
\((\sin\theta + \cos\theta)^2 + (\sin\theta – \cos\theta)^2\) の値を求めなさい。
解答・解説
この式を展開します。
\((\sin\theta + \cos\theta)^2 = \sin^2\theta + 2\sin\theta\cos\theta + \cos^2\theta\)
\((\sin\theta – \cos\theta)^2 = \sin^2\theta – 2\sin\theta\cos\theta + \cos^2\theta\)
これらを足し合わせます。
式 = \((\sin^2\theta + 2\sin\theta\cos\theta + \cos^2\theta) + (\sin^2\theta – 2\sin\theta\cos\theta + \cos^2\theta)\)
\(= \sin^2\theta + \cos^2\theta + \sin^2\theta + \cos^2\theta\)
(\(2\sin\theta\cos\theta\) と \(-2\sin\theta\cos\theta\) は打ち消し合って 0 になります)
ここで、三角比の基本公式 \(\sin^2\theta + \cos^2\theta = 1\) を使います。
式 = \(1 + 1 = 2\)
この結果は \(\theta\) の値に関わらず常に成り立ちます。
答え:2
三角比の正弦定理・余弦定理
△ABCにおいて、A=45°, B=60°, a=6 のとき、辺bの長さを求めよ。
解答・解説
2つの角と1つの辺がわかっている場合、正弦定理を使って他の辺の長さを求めることができます。 正弦定理は a/sinA = b/sinB = c/sinC です。
- 正弦定理を立てる 問題の条件から、
a/sinA = b/sinBの関係を使います。6/sin45° = b/sin60° - bについて解く
b = 6 × (sin60° / sin45°) - sinの値を代入して計算する
sin45° = 1/√2,sin60° = √3/2なので、b = 6 × ( (√3/2) / (1/√2) )b = 6 × (√3/2) × √2b = 3√6
【答え】 b = 3√6
△ABCにおいて、a=2, b=√6, A=45° のとき、角Bの大きさを求めよ。
解答・解説
2つの辺とその片方の対角がわかっている場合、正弦定理を使って他の角の大きさを求めることができます。
- 正弦定理を立てる
a/sinA = b/sinBの関係を使います。2/sin45° = √6/sinB - sinBについて解く
2sinB = √6 sin45°sinB = (√6 / 2) × sin45° - sinの値を代入して計算する
sin45° = 1/√2なので、sinB = (√6 / 2) × (1/√2)sinB = √3 / 2 - Bの値を求める
sinB = √3/2となる角Bは、B = 60°またはB = 120°です。 ここで、A+B < 180° である必要があります。B = 60°の場合、A+B = 45°+60° = 105° < 180°なので、三角形は成立します。B = 120°の場合、A+B = 45°+120° = 165° < 180°なので、こちらも三角形は成立します。
b>aならばB>Aであることから角度を絞り込める場合もありますが、この問題では両方とも解となります。)
【答え】 B = 60° または 120°
△ABCにおいて、C=135°, c=4√2 のとき、この三角形の外接円の半径Rを求めよ。
解答・解説
外接円の半径Rは、正弦定理 a/sinA = 2R を使って求めることができます。
- 正弦定理を立てる 角Cと辺cがわかっているので、
c/sinC = 2Rの関係を使います。(4√2) / sin135° = 2R - Rについて解く
R = (4√2) / (2 sin135°) - sinの値を代入して計算する
sin135° = 1/√2なので、R = (4√2) / (2 × 1/√2)R = (4√2 × √2) / 2R = 8 / 2 = 4
【答え】 R = 4
△ABCにおいて、b=4, c=5, A=60° のとき、辺aの長さを求めよ。
解答・解説
2辺とその間の角がわかっている場合、余弦定理を使って残りの辺の長さを求めることができます。 余弦定理は a² = b² + c² - 2bc cosA です。
- 余弦定理に値を代入する
a² = 4² + 5² - 2 × 4 × 5 × cos60° - cosの値を代入して計算する
cos60° = 1/2なので、a² = 16 + 25 - 2 × 4 × 5 × (1/2)a² = 41 - 20a² = 21 - aの値を求める 辺の長さは正なので、
a = √21
【答え】 a = √21
△ABCにおいて、a=√13, b=3, c=4 のとき、角Aの大きさを求めよ。
解答・解説
3辺の長さがわかっている場合、余弦定理を使って角の大きさを求めることができます。 余弦定理の変形版 cosA = (b² + c² - a²) / 2bc を使います。
- 余弦定理に値を代入する
cosA = (3² + 4² - (√13)²) / (2 × 3 × 4) - 値を計算する
cosA = (9 + 16 - 13) / 24cosA = 12 / 24cosA = 1/2 - Aの値を求める
cosA = 1/2となる角Aは、0° < A < 180°の範囲でA = 60°です。
【答え】 A = 60°
△ABCにおいて、a=2√3, c=2, B=150° のとき、辺bの長さと角Cの大きさを求めよ。
解答・解説
2辺とその間の角がわかっているので、まず余弦定理で残りの辺bを求め、次に正弦定理で角Cを求めます。
- 余弦定理で辺bを求める
b² = a² + c² - 2ac cosBb² = (2√3)² + 2² - 2 × (2√3) × 2 × cos150°cos150° = -√3/2なので、b² = 12 + 4 - 8√3 × (-√3/2)b² = 16 + (8 × 3 / 2)b² = 16 + 12 = 28b = √28 = 2√7 - 正弦定理で角Cを求める
c/sinC = b/sinB2/sinC = (2√7)/sin150°sinC = (2 × sin150°) / (2√7)sin150° = 1/2なので、sinC = (2 × 1/2) / (2√7)sinC = 1 / (2√7) = √7 / 14sinC = √7 / 14となるような有名な角度はないため、解答はこのままで構いません。
【答え】 b = 2√7, sinC = √7 / 14
△ABCにおいて、a=√2, b=2, A=30° のとき、残りの辺cの長さと角B, Cの大きさを求めよ。
解答・解説
2辺とその片方の対角がわかっている場合、正弦定理で他の角を求めます。このとき解が2つ存在する可能性があるので注意が必要です。
- 正弦定理で角Bを求める
a/sinA = b/sinB√2 / sin30° = 2 / sinB√2 sinB = 2 sin30°sinB = (2 × 1/2) / √2 = 1/√20° < B < 180°の範囲でB = 45°またはB = 135° - 場合分けしてcとCを求める
- (i) B = 45° の場合
C = 180° - (A + B) = 180° - (30° + 45°) = 105°正弦定理c/sinC = a/sinAを使ってcを求める。c / sin105° = √2 / sin30°c = (√2 × sin105°) / (1/2) = 2√2 sin105°sin105° = sin(60°+45°) = sin60°cos45° + cos60°sin45° = (√3/2)(√2/2) + (1/2)(√2/2) = (√6+√2)/4c = 2√2 × (√6+√2)/4 = (√12+√4)/2 = (2√3+2)/2 = √3+1 - (ii) B = 135° の場合
C = 180° - (A + B) = 180° - (30° + 135°) = 15°同様にcを求める。c / sin15° = √2 / sin30°c = (√2 × sin15°) / (1/2) = 2√2 sin15°sin15° = sin(45°-30°) = sin45°cos30° - cos45°sin30° = (√2/2)(√3/2) - (√2/2)(1/2) = (√6-√2)/4c = 2√2 × (√6-√2)/4 = (√12-√4)/2 = (2√3-2)/2 = √3-1
【答え】 B = 45°, C = 105°, c = √3+1 または B = 135°, C = 15°, c = √3-1
sinA = sinB cosC を満たす△ABCはどのような形の三角形か。
解答・解説
正弦定理と余弦定理を用いて、式を辺の長さ a, b, c の関係式に直します。外接円の半径をRとします。
- 正弦定理・余弦定理を代入する 正弦定理より
sinA = a/2R,sinB = b/2R余弦定理よりcosC = (a² + b² - c²) / 2abこれらを元の式sinA = sinB cosCに代入します。a/2R = (b/2R) × (a² + b² - c²) / 2ab - 式を整理する 両辺に
2Rを掛けて消去します。a = b × (a² + b² - c²) / 2ab右辺のbを約分します。a = (a² + b² - c²) / 2a両辺に2aを掛けます。2a² = a² + b² - c² - 結論を導く
a² + c² = b²これは三平方の定理の形であり、辺bを斜辺とする直角三角形であることを示しています。
【答え】 B=90° の直角三角形
△ABCにおいて、a=5, b=6, C=45° のとき、この三角形の面積Sを求めよ。
解答・解説
三角形の面積は、2辺とその間の角のsinを使って求めることができます。 面積の公式 S = (1/2)ab sinC を使います。
- 面積の公式に値を代入する
S = (1/2) × 5 × 6 × sin45° - sinの値を代入して計算する
sin45° = √2/2なので、S = (1/2) × 30 × (√2/2)S = 15√2 / 2
【答え】 S = 15√2 / 2
円に内接する四角形ABCDにおいて、AB=2, BC=4, CD=3, DA=2 であるとき、対角線ACの長さと、cos∠ABCの値を求めよ。
解答・解説
対角線ACによって四角形ABCDは、△ABCと△ADCの2つの三角形に分けられます。ACは両方の三角形に共通する辺です。このACの長さを余弦定理で2通りに表します。 また、円に内接する四角形の性質「向かい合う角の和は180°」を利用します (∠ADC = 180° - ∠ABC)。
- △ABCで余弦定理を用いる
AC² = AB² + BC² - 2(AB)(BC)cos∠ABCAC² = 2² + 4² - 2 × 2 × 4 × cos∠ABCAC² = 4 + 16 - 16cos∠ABCAC² = 20 - 16cos∠ABC… ① - △ADCで余弦定理を用いる
AC² = AD² + CD² - 2(AD)(CD)cos∠ADC∠ADC = 180° - ∠ABCなのでcos∠ADC = cos(180° - ∠ABC) = -cos∠ABCAC² = 2² + 3² - 2 × 2 × 3 × (-cos∠ABC)AC² = 4 + 9 + 12cos∠ABCAC² = 13 + 12cos∠ABC… ② - ①と②からcos∠ABCを求める
20 - 16cos∠ABC = 13 + 12cos∠ABC7 = 28cos∠ABCcos∠ABC = 7 / 28 = 1/4 - ACの長さを求める 求めた
cos∠ABCの値を①式に代入します。AC² = 20 - 16 × (1/4)AC² = 20 - 4 = 16AC > 0 なのでAC = 4
【答え】 cos∠ABC = 1/4, AC = 4





コメント