１．三角比の定義
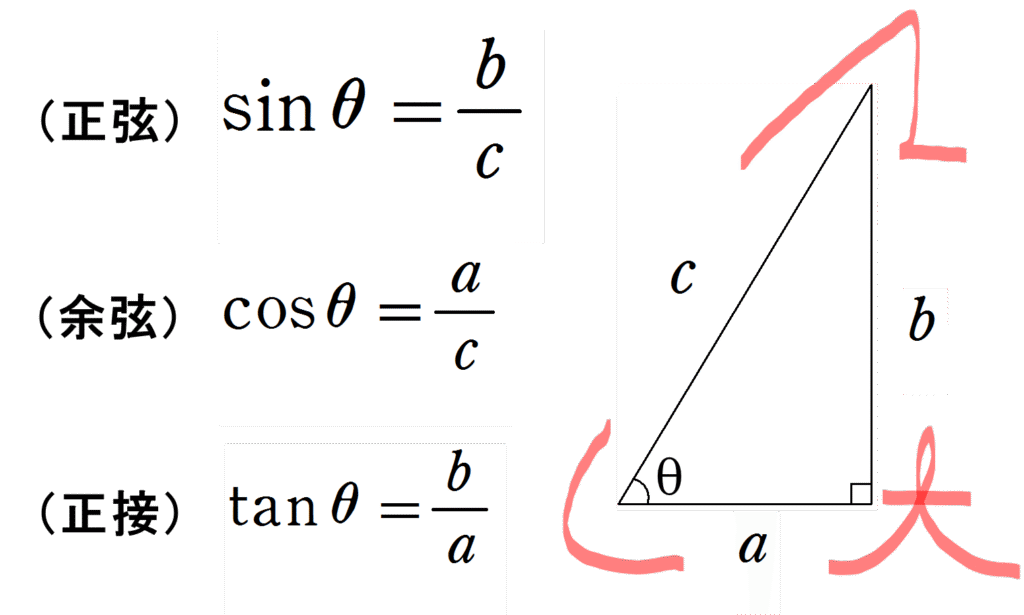
すなわち、
例題
次の直角三角形ABCにおける \(\sin\theta, \cos\theta, \tan\theta\) の値を求めよ。
解答
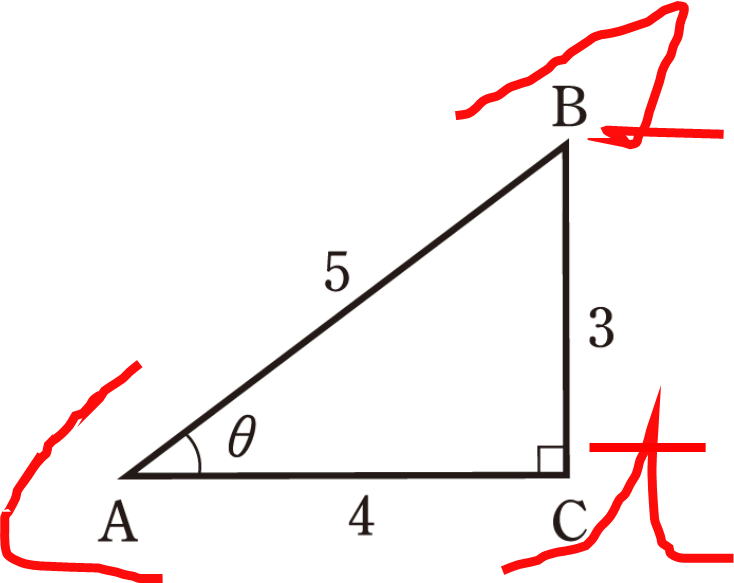
\(\sin\theta=\frac{3}{5}\)
\(\cos\theta=\frac{4}{5}\)
\(\tan\theta=\frac{3}{4}\)
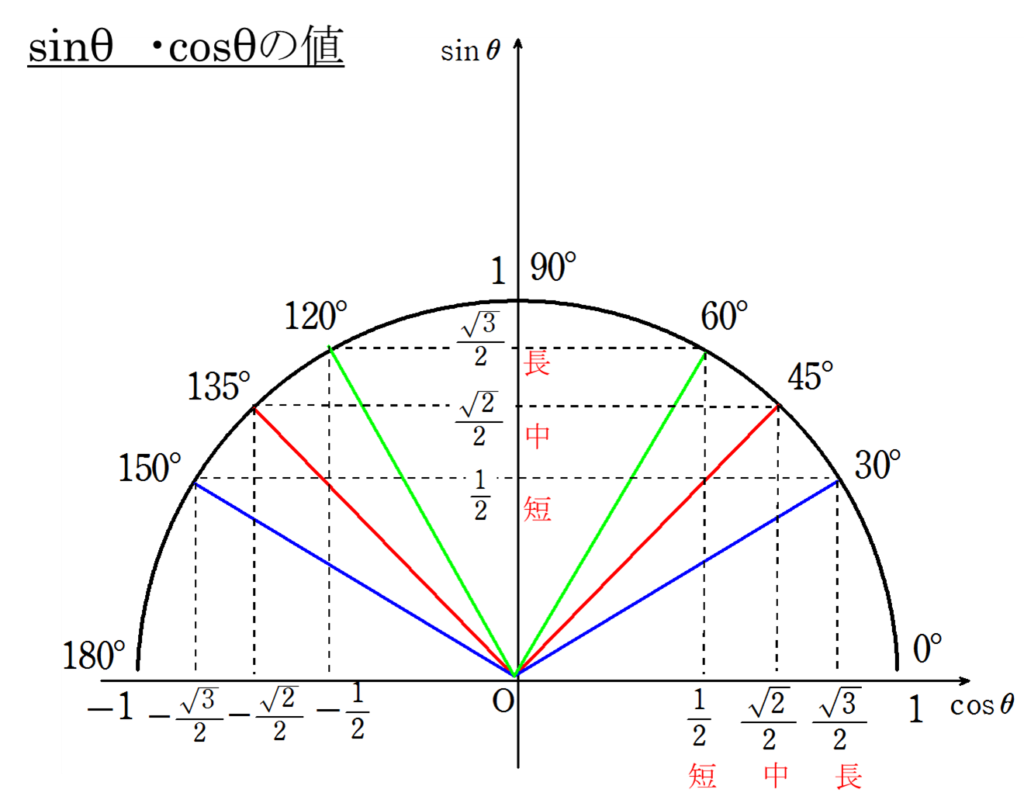
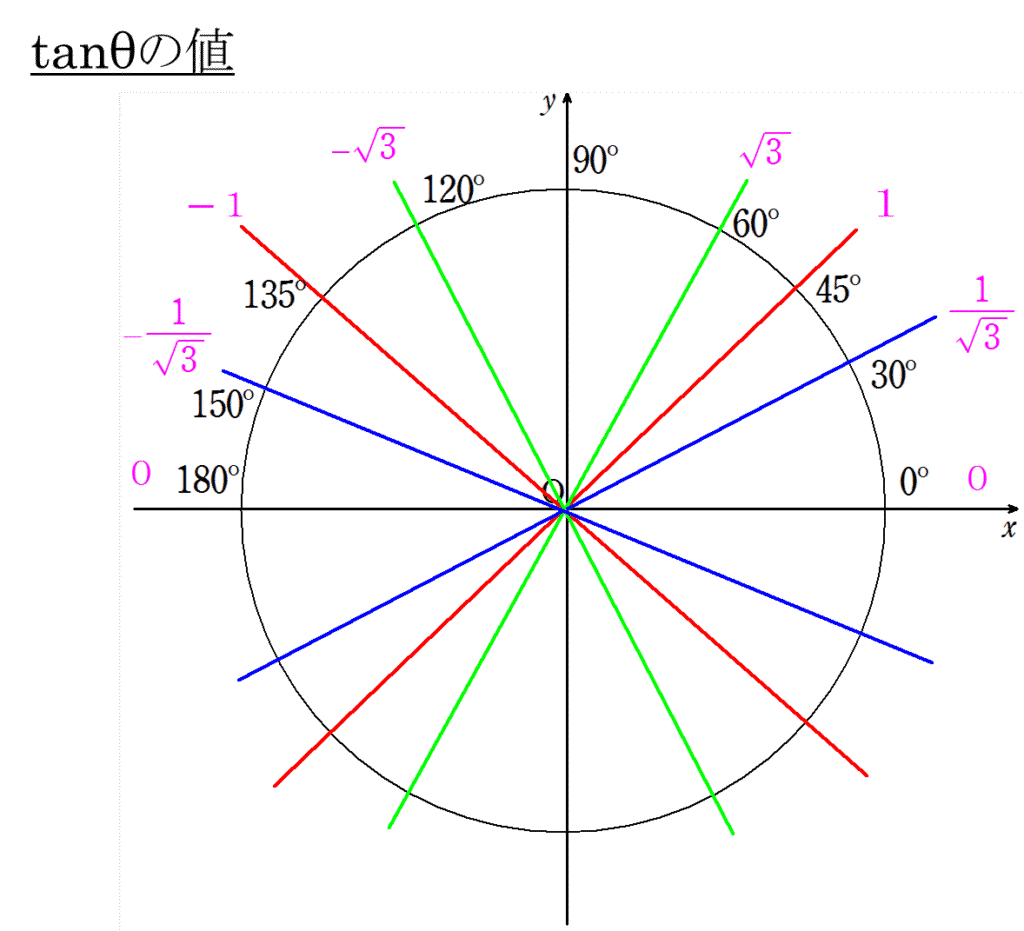
２．三角比の値
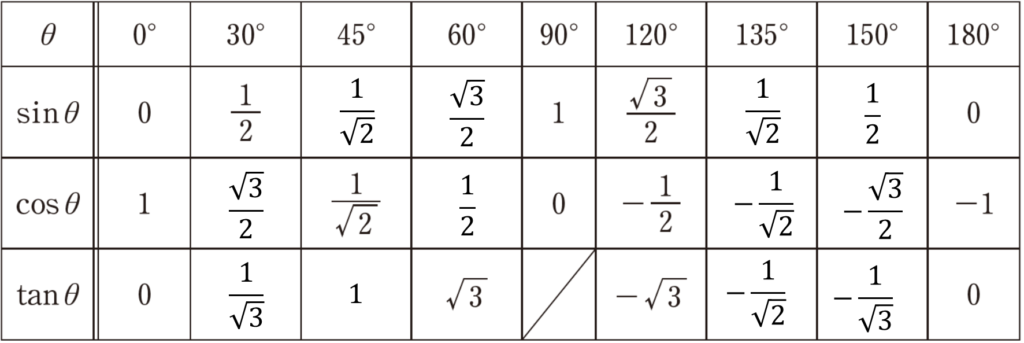
例題
次の値を求めよ。
\(\sin60^{ \circ }\)
\(\cos120^{ \circ }\)
解答
\(\sin60^{ \circ }=\frac{\sqrt{3}}{2}\)
\(\cos120^{ \circ }=-\frac{1}{2}\)
例題
次の値を求めよ。
\(\tan60^{ \circ }\)
解答
\(\tan60^{ \circ }=\sqrt{3}\)
３．90°ーθ,180°ーθの三角比
①\(\sin{(90°-\theta)}=\cos\theta\)
②\(\cos{(90°-\theta)}=\sin\theta\)
③\(\tan{(90°-\theta)}=\frac{1}{\tan\theta}\)
\(\sin{(180°-\theta)}=\sin\theta\)
\(\cos{(180°-\theta)}=-\cos\theta\)
\(\tan{(180°-\theta)}=-\tan\theta\)
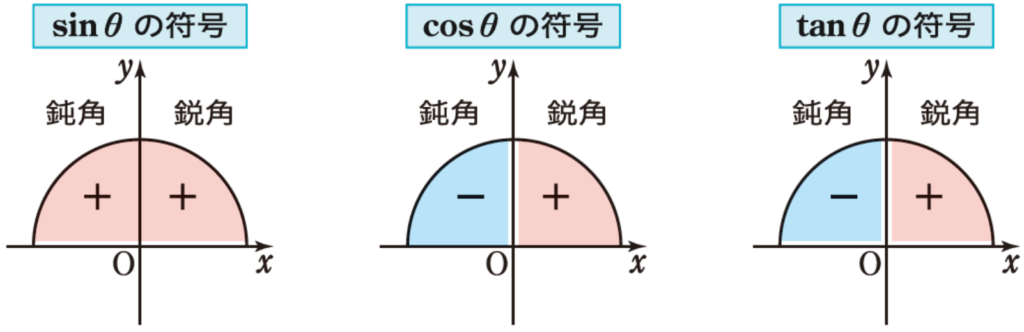
４．三角比の符号
５．三角比の相互関係
①\(tan\theta = \frac{sin\theta}{cos\theta}\)
②\(sin^2 \theta +cos^2 \theta =1 \)
③\(1+tan^2 \theta =\frac{1}{cos^2 \theta}\)
例題
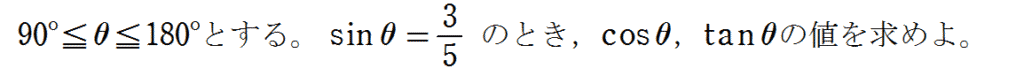
解答
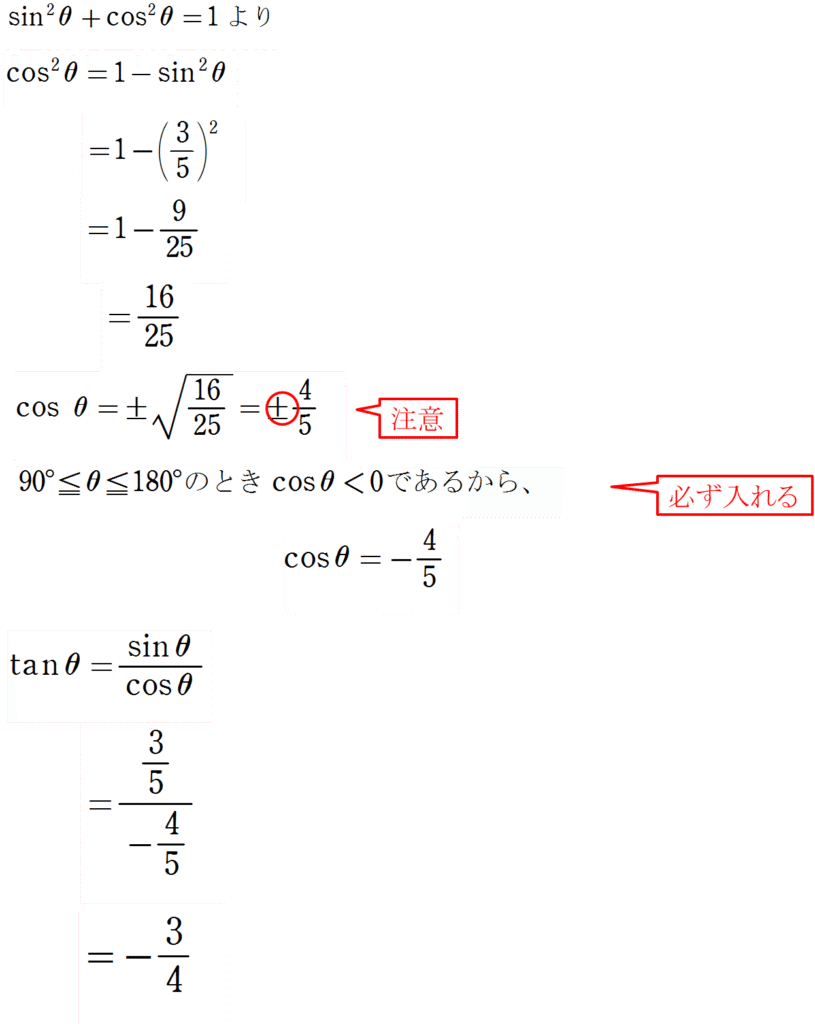
６．正弦定理
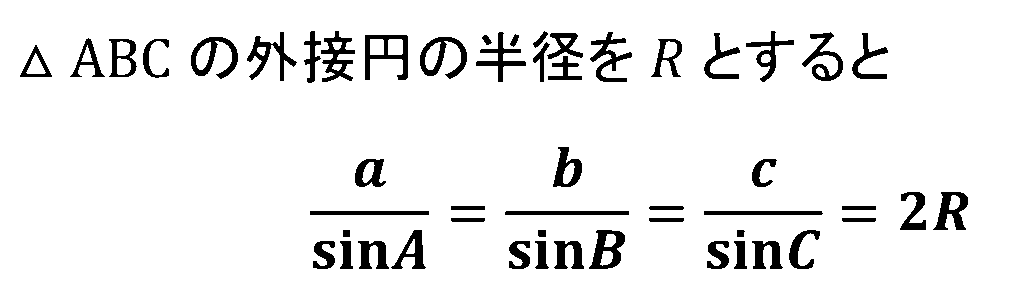
例題
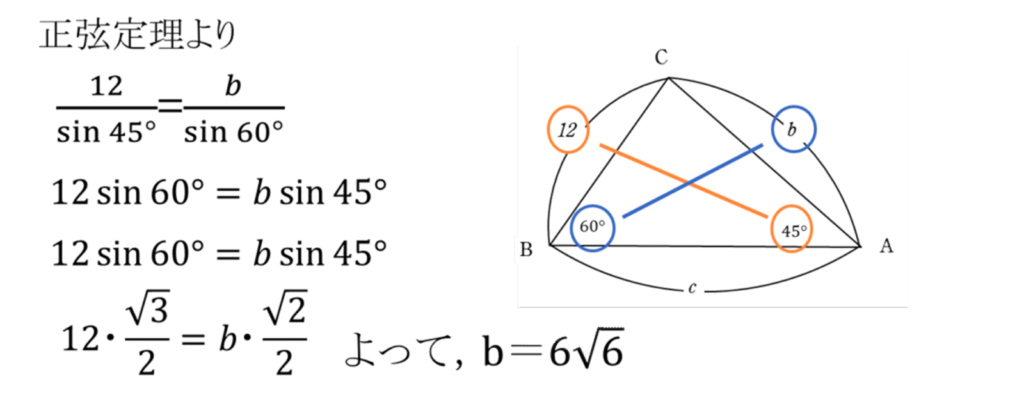
三角形ABCにおいて，
\(a=12, A=45^{\circ}, B=60^{\circ}\) のとき，\(b\)を求めよ。
解答
７．余弦定理
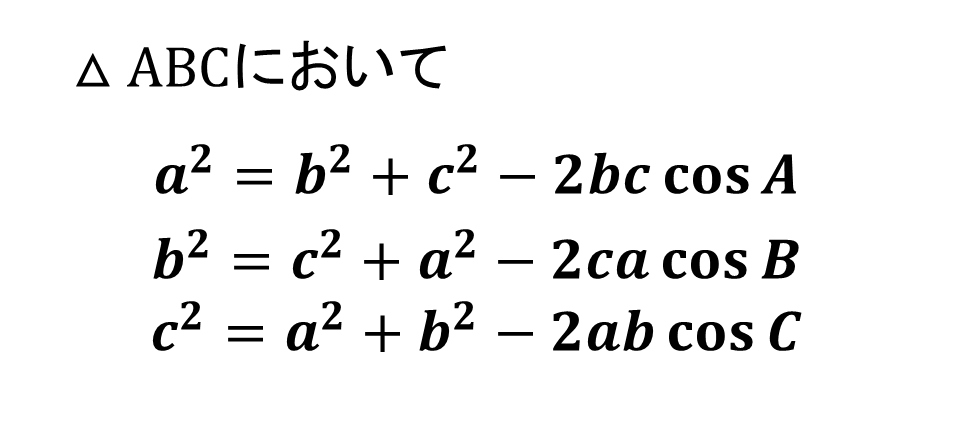
例題
三角形ABCにおいて，\(A=60^{\circ},b=2, c=3\) であるとき，\(a\)を求めよ。
解答
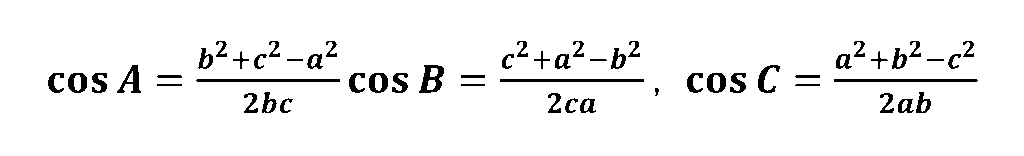
例題
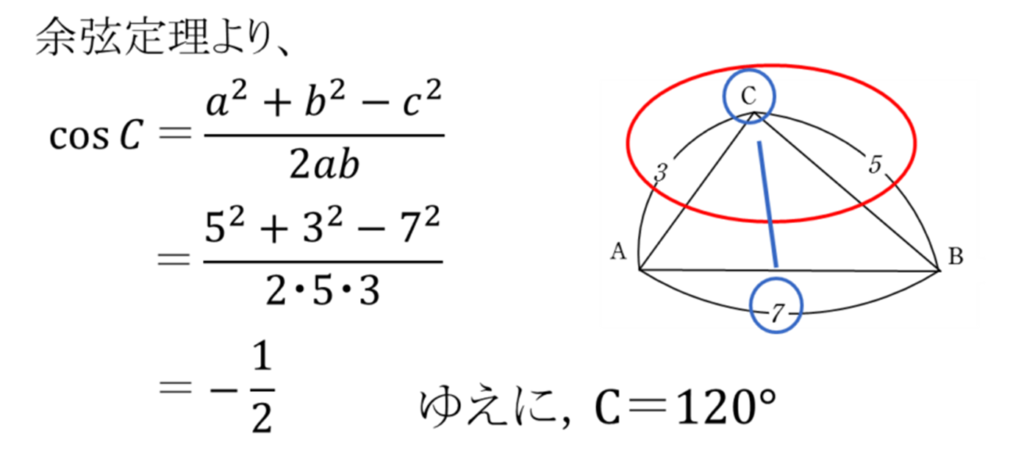
三角形ABCにおいて，\(a=5, b=3, c=7\)のとき\(\angle C\)を求めよ。
解答
８．三角形の面積
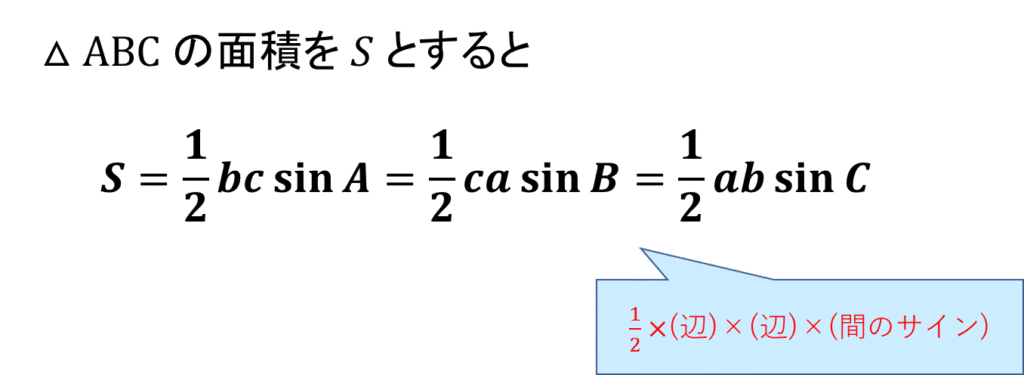
例題
三角形ABCにおいて，\(A=60^{\circ},b=2, c=3\) であるとき，三角形ABCを求めよ。
解答
コメント