ここでは、【数学III】関数の極限でよく利用する公式(基礎知識)や例題を一覧にしてまとめています。
関数の極限〜基本公式・例題一覧〜
1.関数の極限
\(\lim\limits_{x \to a} f(x) = \alpha\), \(\lim\limits_{x \to a} g(x) = \beta\) とする。
① \(\lim\limits_{x \to a} \{k f(x) + l g(x)\} = k\alpha + l\beta\) \((k, l は定数) \)
② \(\lim\limits_{x \to a} f(x) g(x) = \alpha\beta\)
③ \(\lim\limits_{x \to a} \displaystyle\frac{f(x)}{g(x)} = \displaystyle\frac{\alpha}{\beta} (\beta \neq 0)\)
④ \(x\) が \(a\) に近いとき, 常に \(f(x) \leq g(x)\) \(\Rightarrow\) \(\alpha \leq \beta\)
⑤ \(x\) が \(a\) に近いとき, 常に \(f(x) \leq h(x) \leq g(x)\) かつ \(\alpha = \beta\) \(\Rightarrow\) \(\lim\limits_{x \to a} h(x) = \alpha\)
例題
解答
\(\lim\limits_{x \to a} f(x) = \alpha\) \(\iff\) \(\lim\limits_{x \to a} |f(x) – \alpha| = 0 \)
特に \(\lim\limits_{x \to a} f(x) = 0\) \(\iff\) \(\lim\limits_{x \to a} |f(x)| = 0\)
例題
解答
\(\lim\limits_{x \to a + 0} f(x) = \lim\limits_{x \to a – 0} f(x) = \alpha\) \(\iff\) \(\lim\limits_{x \to a } f(x) = \alpha\)
例題
解答
2.基本的な関数の極限
\(\alpha > 0\) のとき \(\lim\limits_{x \to \infty} x^\alpha = \infty\)
\(\alpha < 0\) のとき \(\lim\limits_{x \to \infty} x^\alpha = 0\)
例題
解答
\( \alpha >1\) のとき \(\lim\limits_{x \to \infty} a^x = \infty\),\(\lim\limits_{x \to -\infty} a^x = 0\)
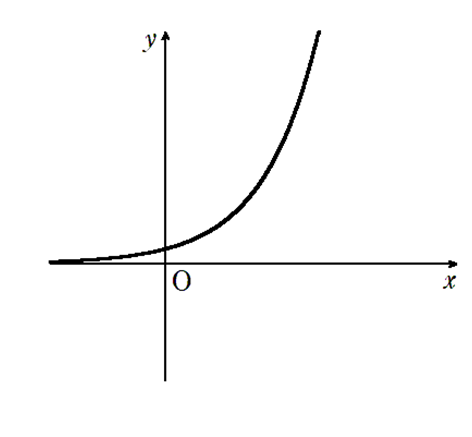
\( 0 < \alpha < 1\) のとき \(\lim\limits_{x \to \infty} a^x = 0\),\(\lim\limits_{x \to -\infty} a^x = \infty\)
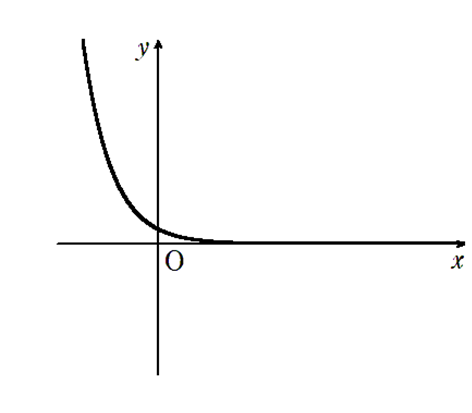
例題
解答
\( \alpha >1\) のとき \(\lim\limits_{x \to \infty} \log_a x = \infty\),\(\lim\limits_{x \to +0} \log_a x = -\infty\)
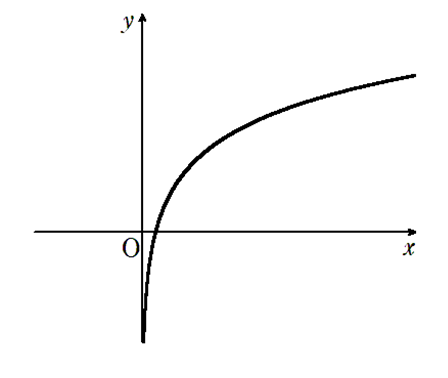
\( 0 < \alpha < 1\) のとき \(\lim\limits_{x \to \infty} \log_a x = -\infty\),\(\lim\limits_{x \to +0} \log_a x = \infty\)
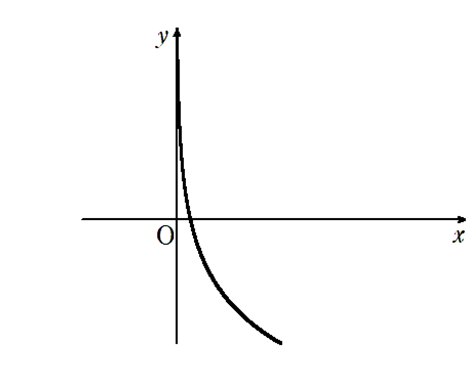
例題
解答
① \(\lim\limits_{x \to 0} \displaystyle\frac{\sin x}{x} = 1\)
② \(\lim\limits_{x \to 0} \displaystyle\frac{x}{\sin x} = 1\)
例題
解答
3.連続な関数の性質
定義域の \(x\) の値 \(a\) に対して, \(\lim\limits_{x \to a} f(x) = f(a)\) のとき, \(f(x)\) は \(x = a\) で連続
例題
解答
閉区間 \([ a, b]\) で連続な関数 \(f(x)\) について
・\(f(x)\) はこの区間で\(f(a)\) と \(f(b)\) の間の任意の値をとる。
・\(f(a)\) と \(f(b)\) が異符号ならば, 方程式 \(f(x) = 0 \) は \(a < x < b\) の範囲に少なくとも1つの実数解をもつ。





コメント