- 逆・対偶・裏とは
- 逆・対偶・裏の具体例と真偽の関係性
- 逆・対偶・裏を用いた問題例
逆・対偶・裏について解説
逆・対偶・裏とは
命題 \( p ⇒ q\) に対して
逆:\( q ⇒ p\)
対偶:\( \overline{ q } ⇒ \overline{ p }\)
裏:\( \overline{ p } ⇒ \overline{ q }\)
と定義します。
 シンスケ
シンスケ「条件AならばB」があったとき、
逆 ⇒ AとBを入れ替える
裏 ⇒ AとBを否定にする
対偶⇒ 逆かつ裏にする
と考えます。
逆・対偶・裏の図のイメージ
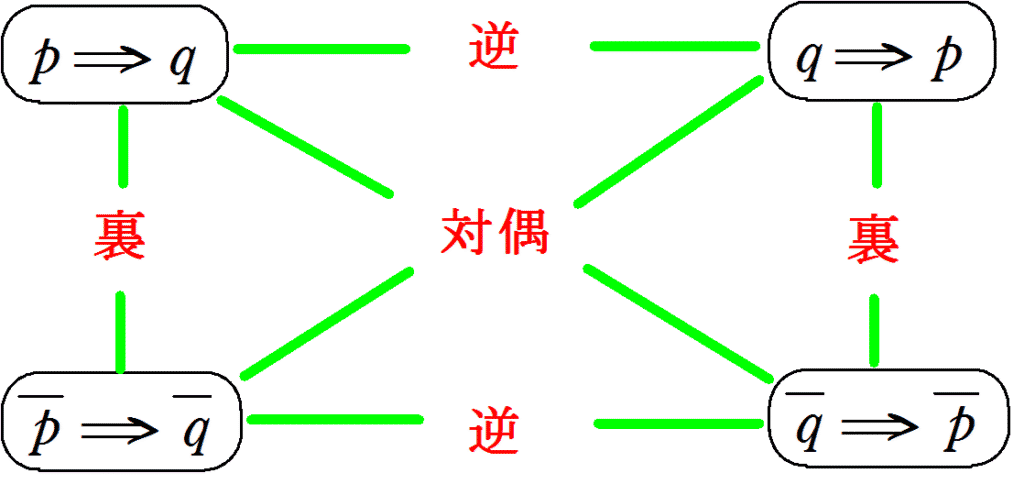

逆・対偶・裏の具体例と真偽の関係性
例えば、男性であるA先生がいたとします。
命題:「A先生 ⇒ 男性」
この命題は「真」です。
このとき、この命題の逆・対偶・裏の真偽がどうなるか考えてみましょう。
逆:「男性 ⇒ A先生」
対偶:「男性ではない ⇒ A先生ではない」
裏: 「A先生ではない ⇒ 男性ではない」
逆の真偽
まず、
逆:「男性 ⇒ A先生」
に関しては、一般的には成り立ちませんね。



男性全員がA先生ではありません(反例がある)
したがって、この命題の逆に関しては「偽」となります。
すなわち、
という点に注意しましょう。
※同様に、元の命題が「偽」であっても逆は「真」になることも「偽」になることもあります。
裏の真偽
続いて、裏がどうなるかみていきましょう。
裏:「A先生ではない ⇒ 男性ではない」
これも、逆の場合と同様に、A先生ではない人の中にも男性はおりますので、必ずしも成り立つとは限りません。
したがって、この命題の裏に関しては「偽」となります。
すなわち、裏に関しても
とということが成り立ちます。
※同様に、元の命題が「偽」であっても裏は「真」になることも「偽」になることもあります。
対偶の真偽
最後に、対偶をみていきましょう。
対偶:「男性ではない ⇒ A先生ではない」
これは、成り立ちますね。
一般的に条件\(p, q\) を満たす全体の集合を\(P, Q\) とし、全体集合を\(U\) とすると、
\(P \subset Q ⇒ \overline{Q} \subset \overline{P}\)
が以下の図の通り成り立ちます。
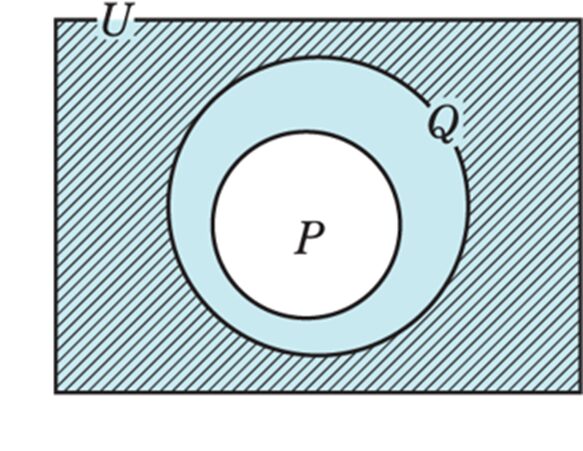




\(\overline{ q }\)は \(\overline{ p }\) に完全に含まれるため部分集合となります。
したがって、
ということがいえます。
したがって、特に証明問題において、
命題\(p ⇒ q\) を証明するにはその対偶\( \overline{ q } ⇒ \overline{ p }\)を証明してもOKです。


例題
\(n\)を自然数とするとき,次の命題の真偽を調べよ。
また,その逆,対偶,裏を述べ,それらの真偽を調べよ。
\(n\)は\(4\)の倍数である\(\Rightarrow\) \(n\) は\(2\) の倍数である
解答
\(n\)が4の倍数であるとき、必ず2の倍数になるため、命題は真である
また、この命題の逆,対偶,裏は以下のようになる
逆:\(n\)は\(2\)の倍数である\(\Rightarrow\) \(n\) は\(4\) の倍数である 偽(反例:\(n=6\))
対偶:\(n\)は\(2\)の倍数でない\(\Rightarrow\) \(n\) は\(4\) の倍数でない 真
裏:\(n\)は\(4\)の倍数でない\(\Rightarrow\) \(n\) は\(2\) の倍数でない 偽(反例:\(n=6\))
対偶を利用した証明問題
証明問題では「対偶」の性質を利用することで以下のように証明できることがあります。
●対偶の利用
命題\(p \Rightarrow q\) を証明するには, その対偶\(\overline{q} \Rightarrow \overline{p}\)を証明してもよい。
(命題\(p \Rightarrow q\) とその対偶\(\overline{q} \Rightarrow \overline{p}\)の真偽は一致する)
例題
\(n\)は整数とする。\(n^2\)が\(3\)の倍数でないならば,\(n\)は\(3\)の倍数でないことを証明せよ。
解答
対偶:「\(n\)が3の倍数ならば,\(n^2\)は3の倍数である」
ことを示せばよい。
\(n\)が\(3\)の倍数のとき,\(n=3k\)(\(k\)は整数)とすると,
\(n^2=(3k)^2=9k^2\)
より,3の倍数であるから,成り立つ。
よって、対偶が成り立つから元の命題も成り立つ。





コメント