- 集合と要素とは
- 要素の表し方
- 集合の表し方
- 部分集合とは
- 共通部分・和集合とは
- 補集合とは
- ド・モルガンの法則
集合と要素
集合と要素とは
例えば
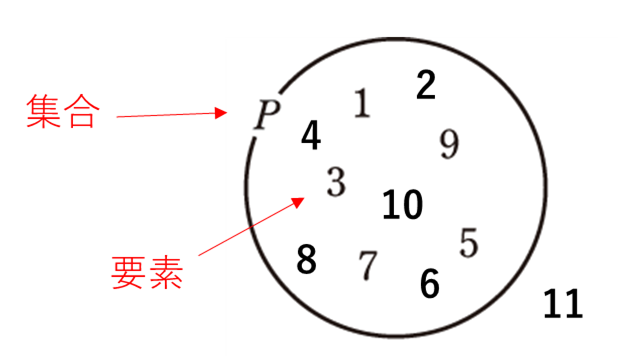
「1から10までの自然数の集まり」
のように
数やものの集まりのことを集合、集合を構成している1つ1つのものをその集合の要素といいます。
 シンスケ
シンスケ上記の例の場合だと、要素は「1」、「3」、「6」など1から10までのそれぞれの自然数となります。
要素の表し方
\(a\) が集合 \(A\) の要素であることを
\(a \in A\)
と表し、\(a\) は集合 \(A\) に属するといいます。
また、逆に \(a\) が集合 \(A\) の要素でない場合は
\(a \notin A\)
と表します。
例えば、
「1から10までの自然数の集まり」
の集合を \(P\) とすると
\(2 \in P\), \( 11 \notin P\)
となります。

集合の表し方
集合の表し方には,2種類あります。
パターン①:要素を書き並べる方法
集合の表し方の1つ目は「要素を書き並べる方法」です。
例
① 1から5までの自然数 \(A = \{1, 2, 3, 4, 5\}\)
② 3で割り切れる自然数全体の集合\(B = \{3, 6, 9, 12, 15, \cdots\cdots\}\)



集合\(B\) のように要素の個数が多い場合は「\(\cdots\cdots\)」を使うことで表します。
パターン②:要素の満たす条件を書く方法
「要素を書き並べる方法」でも集合は表せますが、この方法だと細かな条件をつけることができないため、不便なことが多くあります。
そこで、集合の表し方のもう1つに「要素の満たす条件を書く方法」があります。
例えば、パターン①で紹介した例①②は「要素の満たす条件を書く方法」で表すと以下のようになります。
例
① 1から5までの自然数 \(A = \{n| 1\leq n \leq 5, n は自然数\}\)
② で割り切れる自然数全体の集合\(B = \{3x|x = 1, 2, 3, \cdots\cdots\}\)
上記のように要素の代表を\(n\), \(3x\) のように表し、 縦線の右にその要素が満たす条件を記載します。



パターン②に関しては、適宜パターン①に直せるようにしておきましょう。
直し方としては、以下のように縦線の右から左に向かって
「(右側部分の条件)を満たす(左側)の集合」
と解釈すればOKです。
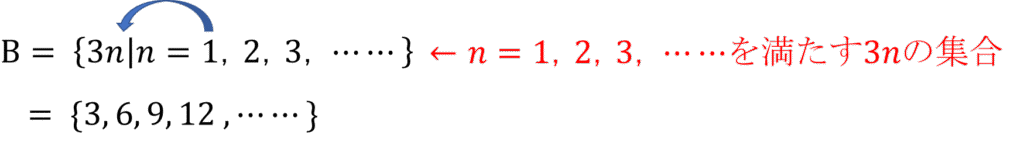
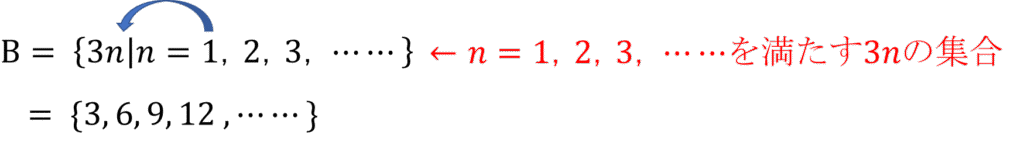
部分集合
2つの集合\(A , B\) において、
\(A\) のどの要素も \(B\) の要素になっているとき,
すなわち
\(x \in A\) ならば \(x \in B\)
が成り立つとき、\(A\) は \(B\) の部分集合といい、
\(A \subset B\)
と表します。
例
\(A = \{1, 3, 5\} ,B = \{1, 2, 3, 4, 5\}\) のとき、\(A\) のどの要素も\(B\) の要素であるため
\(A \subset B\)
である
空集合
要素を1つも持たない集合を空集合といい、\(\emptyset\)で表します。
空集合は任意の集合\(A\) に対して部分集合、すなわち
\(\emptyset \subset A\)
となります。
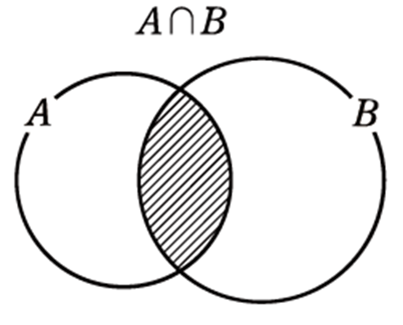
共通部分と和集合
\(A, B\) のどちらにも属する要素全体の集合

例題
\(A=\{1, 2, 5, 7\}, B=\{0, 1, 5, 8\} \)において,\(A \cap B\) を求めよ。
解答
\(A \cap B=\{1, 5\}\)
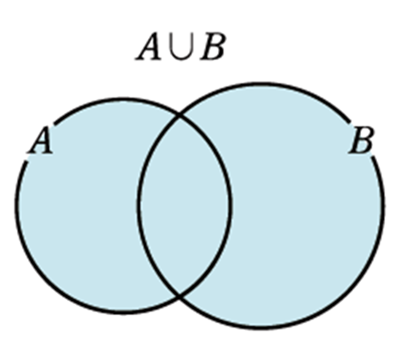
\(A, B\) の少なくとも一方に属する要素全体の集合

例題
\(A=\{1, 2, 5, 7\}, B=\{0, 1, 5, 8\} \)において,\(A \cup B\) を求めよ。
解答
\(A \cup B=\{0,1,2,5,7,8\}\)
補集合
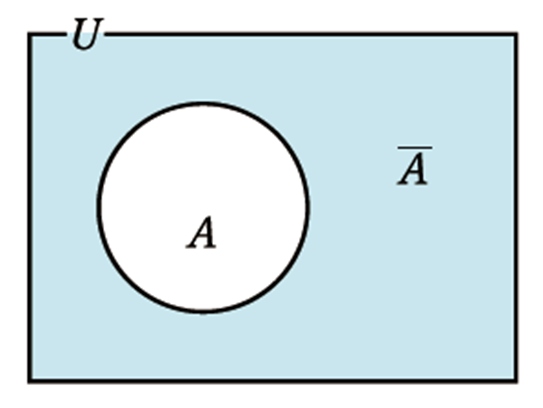
全体集合\(U\)の部分集合\(A\)に対して、\(U\)の要素で,\(A\)には属さない要素全体の集合

例題
\(U=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}\)を全体集合とするとき,
\(U\)の部分集合\(A=\{1,2,3,5,7,9\}\)において補集合\(\overline{A}\)を求めよ。
解答
\(\overline{A}=\{4,6,8\}\)



補集合\(A\)は\(A\) 以外の集合になります。
ド・モルガンの法則
\(A \cap B , A \cup B\) の補集合について、それぞれ次の法則が成り立ちます。
① \(\overline{ A\cap B } =\overline{ A }\cup \overline{ B }\)
② \(\overline{ A\cup B } =\overline{ A }\cap \overline{ B }\)
例題
\(U=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}\)を全体集合とする。\(U\)の部分集合\(A\),\(B\)について
\(A \cup B=\{1,2,5,7,8\}\)であるとき, 集合\(\overline{A}\cap \overline{B}\)を求めよ。
解答
\(\overline{A}\cap \overline{B}=\overline{A \cup B}=\{3,4,6,9\}\)





コメント