- 「命題」「条件」「仮定」「結論」
- 命題の真偽の判定方法と「反例」
- 「必要条件」「十分条件」
- 条件の否定
命題と条件~必要条件・十分条件~
命題とは
正しいか正しくないかが明確に決まる文や式のことを命題といいます。
例えば、次のような2文があったとします。
① \(x\) を実数とするとき、\(x = 3\) ならば \(x^2 = 9\) である。
② \(x\) を実数とするとき、\(x^2 = 9\) ならば \(x = 3\) である。
①は明らかに「正しい」ことがわかるかと思います。
それに対して、②は
\(x^2 = 9\) は \(x = \pm 3\)
であるため、\(x = -3\) のときも成り立つため、「正しくない」 ことがわかります。
したがって、①②ともに正しいか正しくないかがはっきりしますので命題です。
①のように命題が正しいとき「真」、②のように命題が正しくないとき「偽」といいます。
条件とは
例えば
「\(x\) は1より大きい数である」
という文があった場合、
\(x\) の値によっては真になる場合も、偽になる場合もあります。
 シンスケ
シンスケ実際、\(x = 3\) ならば真、\(x = – 1\) ならば偽ですね。
このような文字 \(x\) を含んだ 文や式を\(x\) に関する条件といいます。
仮定と結論とは
① \(x\) を実数とするとき、\(x = 3\) ならば \(x^2 = 9\) である。
② \(x\) を実数とするとき、\(x^2 = 9\) ならば \(x = 3\) である。
のように、命題は2つの条件\(p, q\) を用いて「\(p\) ならば \(q\)」の形でほとんどの場合表されます。
命題「\(p\) ならば \(q\)」を \(p ⇒ q\) と表し、\(p\) を仮定、\(q\) を結論といいます。
また、「\(p ⇒ q\)」かつ「\(q ⇒ p\)」を \(p ⇔ q\) と表します。
命題の真偽
全体集合を \(U\) とする命題「\(p ⇒ q\)」において、
条件\(p\) の満たす\(U\) の要素全体の集合を \(P\) ,
条件\(q\) の満たす\(U\) の要素全体の集合を \(Q\) ,
とするとき
命題「\(p ⇒ q\)」が真であることと\(P \subset Q\) が成り立つことは同じ
になります。
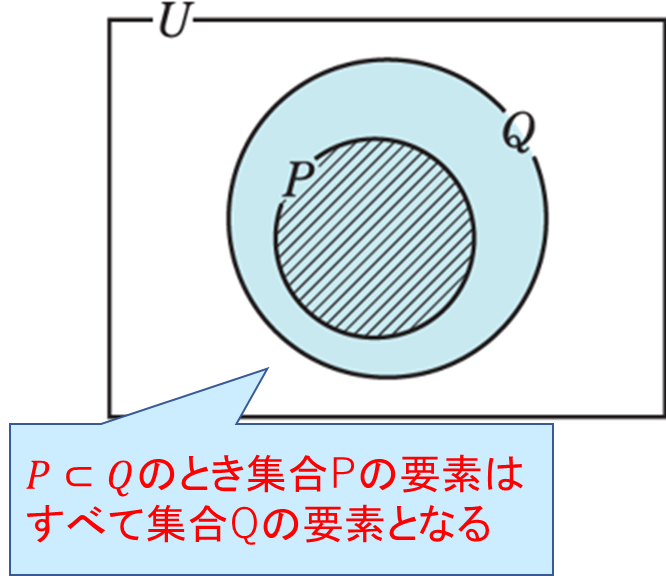

また、
命題「\(p ⇔ q\)」が真であることと\(P = Q\) が成り立つことは同じ
となります。
したがって、命題「\(p ⇒ q\)」の真偽を確かめるためには\(P \subset Q\) かどうかを調べればOKです。
反例
上記から
命題「\(p ⇒ q\)」が偽であるとき\(P \not \subset Q\)
となります。
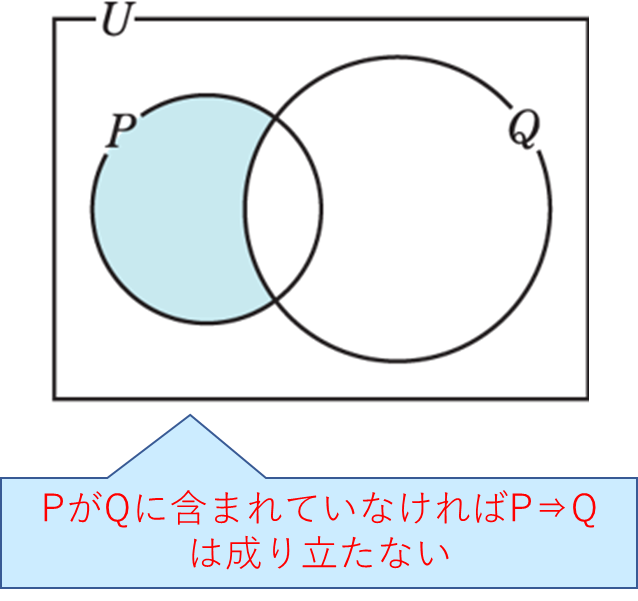

したがって、命題「\(p ⇒ q\)」が偽であるときは、仮定\(p\) は満たすが \(q\) を満たさないものがあります。
このような要素をこの命題の反例といいます。
一般的に、命題が偽であることを示すには反例(成り立たない例)をあげればOKです。
例
\(n\) は自然数とする。
「\(n\) は2 の倍数である ⇒ \(n\) は4の倍数である」
において、\(n = 6\) は反例であるから反例であるからこの命題は偽である
必要条件と十分条件
2つの条件\(p, q\)について
① 命題\(p \Rightarrow q\)が真であるとき
\(p\) は\(q\) であるための 十分条件
\(q\) は\(p\) であるための 必要条件
といいます。
② 命題\(p \Rightarrow q\)と(q \Rightarrow p\)がともに真であるとき(すなわち、\(p \Leftrightarrow q\)であるとき)
\(p\) は\(q\) (\(q\)は\(p\))であるための 必要十分条件 (\(p\) と\(q\)は同値)
といいます。
すなわち、以下が成り立ちます。
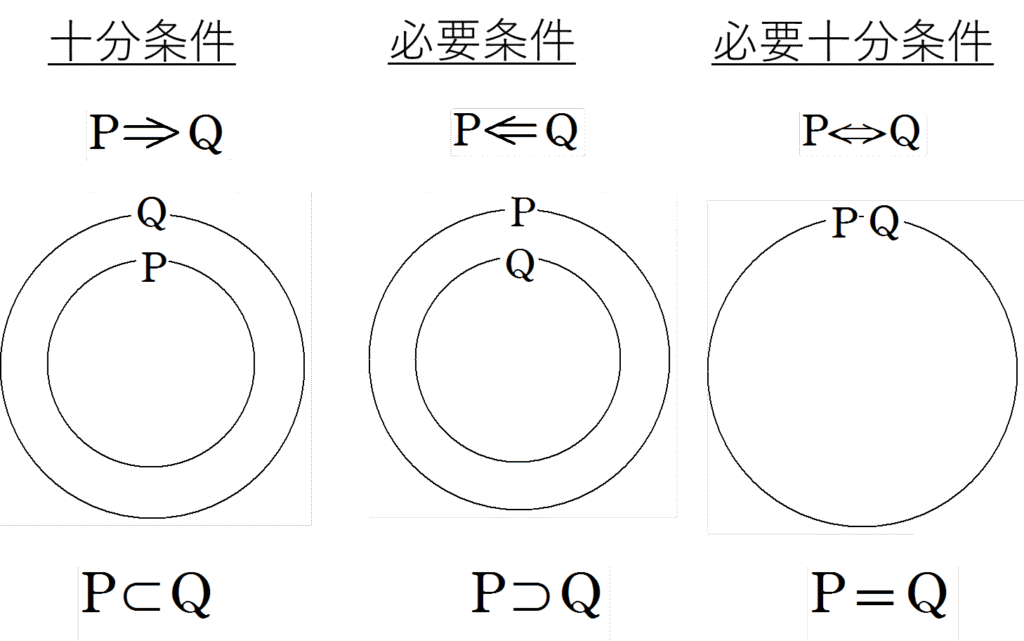

例題
\(x\)は実数とする。
次の□の中は,
「必要条件であるが十分条件でない」,「十分条件であるが必要条件ではない」,「必要十分条件である」,「必要条件でも十分条件でもない」
のうちそれぞれどれが適するか。
① \(x=2\) は\(x^2-5x+6=0\) であるための □。
② \(x=1,2,3\) は \((x-1)(x-2)=0\)であるための □。
③ \(|x|=0\) は \(x=0\) であるための □。
解答
① \(x^2-5x+6=0\)の解は\(x=2, 3\) より
\(x=2 \Rightarrow x^2-5x+6=0 \) は 真
\(x^2-5x+6=0 \Rightarrow x=2 \) は 偽
であるから 「十分条件であるが必要条件ではない」
② \((x-1)(x-2)=0\)の解は\(x=1, 2\)より
\(x=1, 2, 3 \Rightarrow (x-1)(x-2)=0 \) は 偽
\((x-1)(x-2)=0 \Rightarrow x=1, 2, 3 \) は 真
であるから 「必要条件であるが十分条件ではない」
③\(|x|=0\)の解は\(x=0\)より
\(|x|=0 \Rightarrow x=0\) は真
\(x=0 \Rightarrow |x|=0\) は真
であるから 「必要十分条件である」
条件の否定
「条件\(p\)でない」という条件を条件\(p\)の否定といい、\(\overline{p}\) で表します。
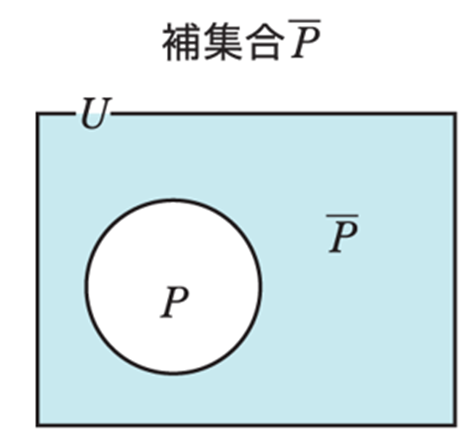

特に、「\(p\) かつ\(q\)」、「\(p\) または\(q\)」の否定はド・モルガンの法則により、以下のようになります。


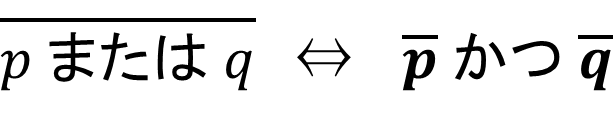
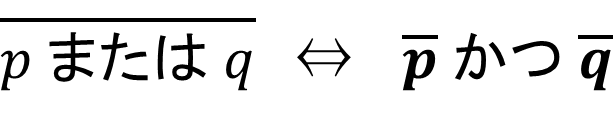
例題
次の条件の否定を求めよ。
\(x<7 または x=2\)
解答
与えられた条件の否定は
\(\overline{x<7} かつ \overline{x=2}\)
より
\(x \geq 7 かつ x \neq 2\)




コメント