ここでは、【中学数学】「図形」分野でよく利用する公式(基礎知識)や例題を一覧にしてまとめています。
1.平面図形
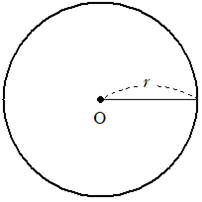
半径 \(r\) の円において, 円周率を\(\pi\) とすると
①円周の長さ \(l = 2 \pi r\)
※(直径)× (円周率)
②円の面積 \(S = \pi r^2\)
※(半径)×(半径)×(円周率)
例題
半径 \(3\) の円について,次の問いに答えよ。円周率を\(\pi\) とする。
(1)円周の長さ \(l\) を求めよ。
(2)円の面積 \(S\) を求めよ。
解答
(1)\(l = 2 \times \pi \times 3 = 6\pi\)
(2)\(S = \pi \times 3^2 = 9\pi\)
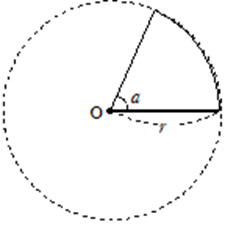
半径 \(r\) 中心角 \(a\) の扇形において,
円周率を\(\pi\) とすると
①弧の長さ \(l = 2 \pi r \times \displaystyle\frac{a}{360^\circ}\)
※円周に対する割合\(\displaystyle\frac{a}{360^\circ}\)を掛けると弧の長さになる
②面積 \(S = \pi r^2 \times \displaystyle\frac{a}{360^\circ }\)
※円の面積に対する割合\(\displaystyle\frac{a}{360^\circ }\)を掛けると扇形の面積になる
例題
半径 \(3\) , 中心角 \(60^{\circ}\) の扇形について, 次の問いに答えよ。円周率を\(\pi\) とする。
(1)弧の長さ \(l\) を求めよ。
(2)面積 \(S\) を求めよ。
解答
(1)\(l = 2 \times \pi \times 3 \times \displaystyle\frac{60^\circ}{360^\circ} = \pi\)
(2)\(S = \pi \times 3^2 \times \displaystyle\frac{60^\circ}{360^\circ}= \displaystyle\frac{3}{2}\pi\)
①\(n\) 角形の内角の和は
\( 180^\circ \times (n -2)\)
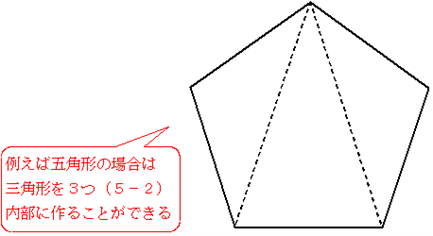
※三角形(内角の和が180°)が\((n – 2)\)個あると考える
②正\(n\)角形の1つの内角の大きさは
\(\displaystyle\frac{1}{n}\{180^\circ \times (n -2)\}\)
※正\(n\)角形はすべての内角の和が等しいため、\(n\) 角形の内角の和を頂点の数\(n\)で割る
例題
正十角形の1つの内角の大きさを求めよ。
解答
\(\displaystyle\frac{1}{10}\{180^\circ \times (10 – 2)\} = 144^{\circ}\)
①3辺の長さがそれぞれ等しい(三辺相等)
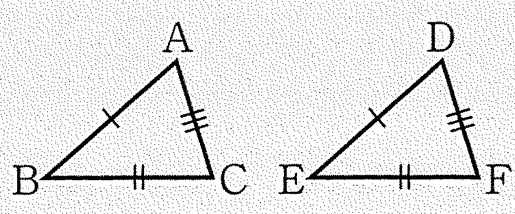
②2辺のその間の角がそれぞれ等しい(二辺挟角相等)
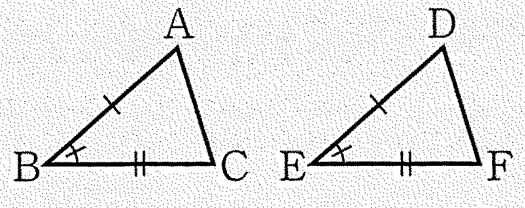
③1辺とその両端の角がそれぞれ等しい(一辺両端角相等)
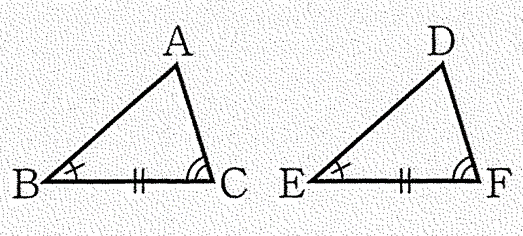
※特に、直角三角形の合同条件は以下になる
①’ 斜辺と1つの鋭角がそれぞれ等しい
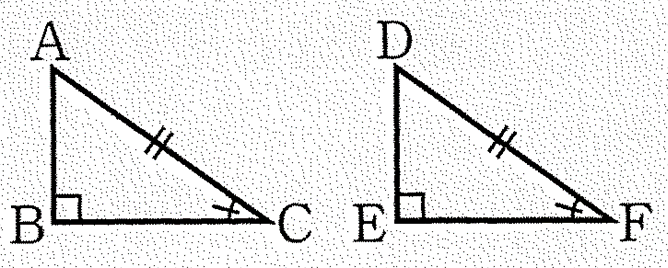
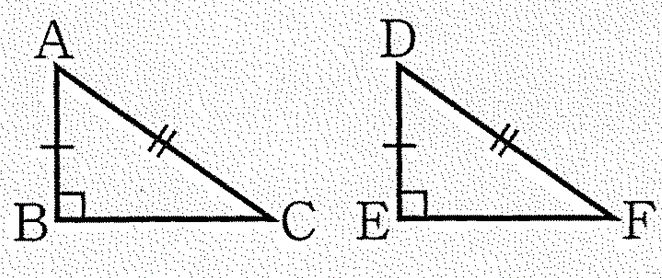
②’ 斜辺と他の1辺がそれぞれ等しい
例題
線分ABと CD が, AP = DP, CP = BPとなるように,点P で交わっている。
このとき,△APC ≡ △DPBであることを証明せよ。
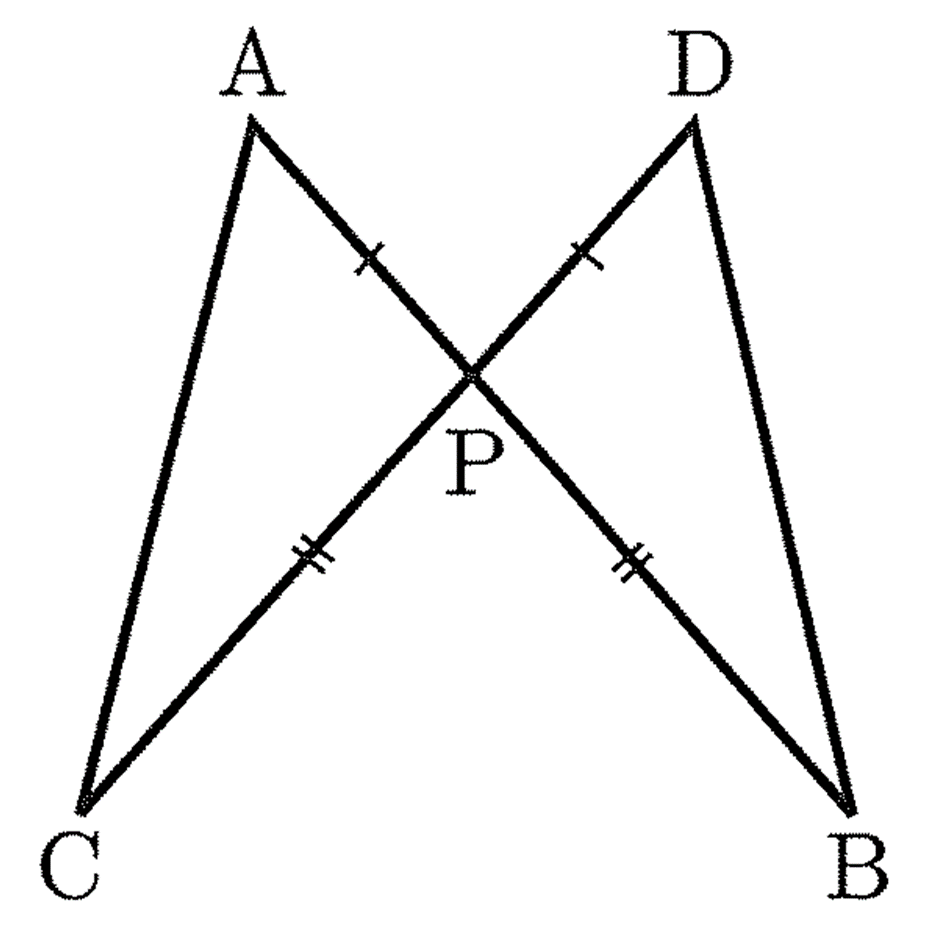
解答
△APC と △DPB において
① AP = DP (仮定より)
② CP = BP(仮定より)
③ ∠APC = ∠DPB(対頂角より)
①、②、③から2組の辺とその間の角がそれぞれ等しいから
△APC ≡ △DPB
①3辺の比がそれぞれ等しい(三辺比相等)
②2辺の比とその間の角が等しい(二辺比挟角相等)
③2つの角がそれぞれ等しい(二角相等)
例題
次の2つの三角形は相似であることを示せ。
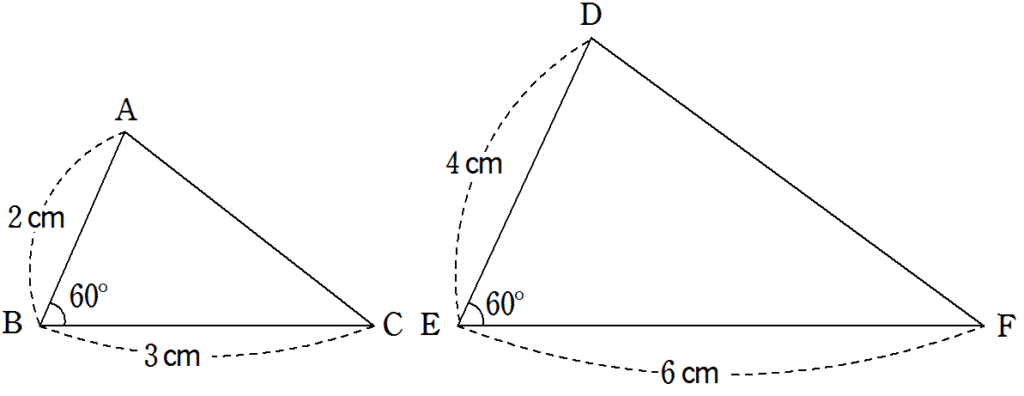
解答
三角形ABCと三角形DEFにおいて
① AB:BC = DE:EF = 2:3
② ∠ABC = ∠DEF = 60°
①、②より、2辺の比とその間の角が等しいから
三角形ABCと三角形DEFは相似である
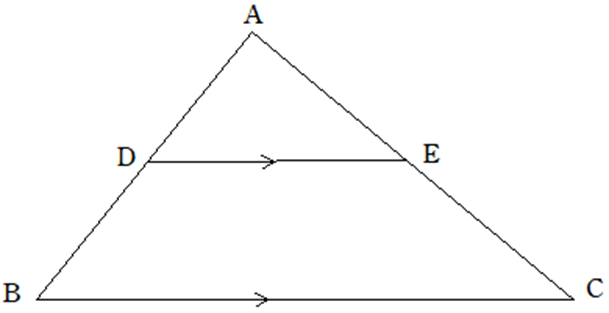
図において、\(DE /\!/ BC\) のとき
①\(AD : AB = AE : AC = DE : BC\)
② \(AD : DB = AE : EC\)
例題
次の図の△ABC において, \(DE /\!/ BC\)のとき, \(x\) の値を求めなさい。
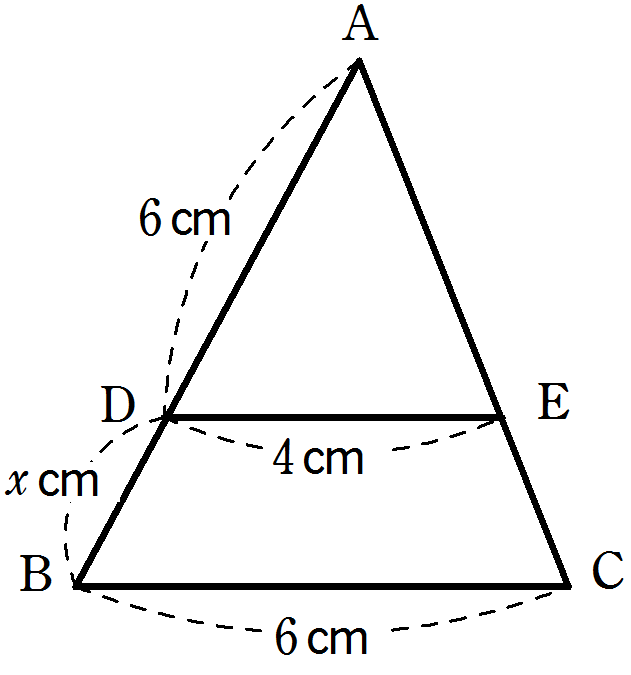
解答
\(DE /\!/ BC\) のとき
△ABC∽△ADE より
AB : AD = BC : DE より,
\(x + 6 : 6 = 6 : 4\)
\(4(x + 6) = 36\)
\(x +6 = 9\)
\(x = 3\)
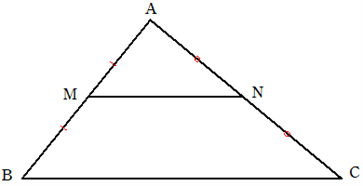
三角形ABCにおいて\(M, N\) がそれぞれ\(AB, AC\) の中点のとき
①\(MN /\!/ BC\)
②\(MN:BC = 1:2\)
例題
次の図の△ABC において, 点D, E は三角形ABCの中点であるとき\(x\) の値を求めなさい。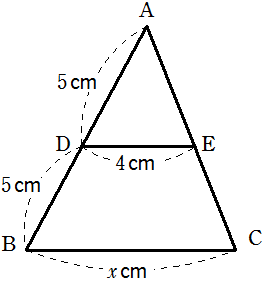
解答
点D,Eが三角形ABCの中点であるとき,中点連結定理より,
\(DE /\!/ BC\) かつ DE : BC = 1 : 2 より,
\(x = 4 \times 2 = 8\)
△ABCの\(\angle\)Aの内角の二等分線と辺BCとの交点Pは,辺BCをAB:ACに内分する
BP:PC=BA:AC

例題
右の図でAPは\(\angle\)Aの内角の二等分線とする。AB=8, AC=6 であるとき,
BP:PCを求めよ。

解答
APは\(\angle\)Aの内角の二等分線より
BP:PC=BA:AC=8:6=4:3
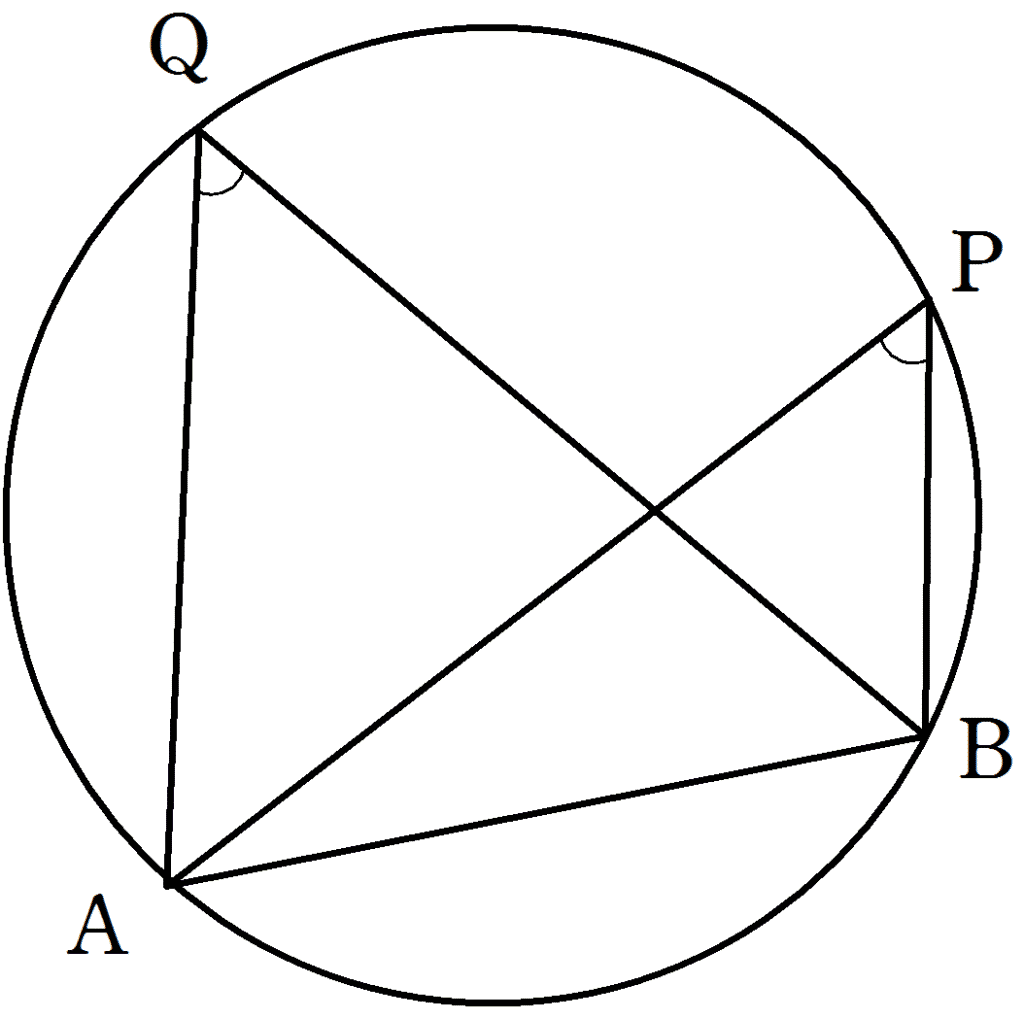
①図において、4点A, B, P, Q が同一円周上にあるとき、
\(\angle\)APB =\(\angle\)AQB
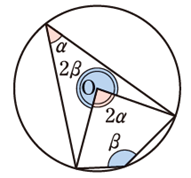
②円周角は中心角の半分
※特に、直径(中心角\(180^\circ\))がつくる円周角は直角(\(90^\circ\))
例題
図において、4点A, B, P, Q が同一円周上にあり、∠AQB = 50° のとき, ∠APBの値を求めよ。
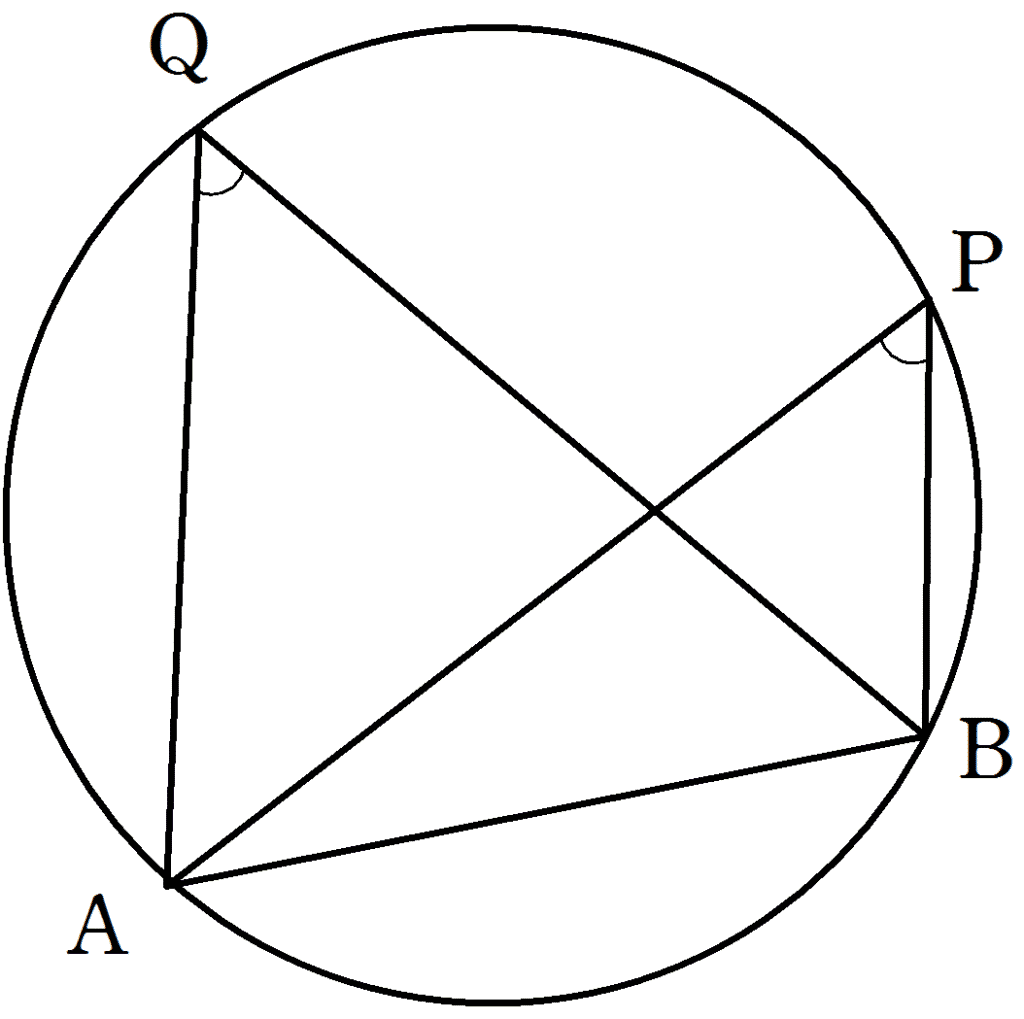
解答
4点A, B, P, Q が同一円周上にあるから、円周角の定理より
\(\angle\)APB =\(\angle\)AQB = 50°
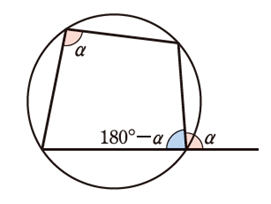
四角形が円に内接するとき、
①対角の和は \(180^\circ\)
②内角は,その対角の外角に等しい
例題
右の図のように,四角形ABCDが円に内接し,
\(\angle\mathrm{BAD} = 113^{\circ}\)です。
このとき,
\(\angle\mathrm{\alpha}\)
の大きさを求めなさい。
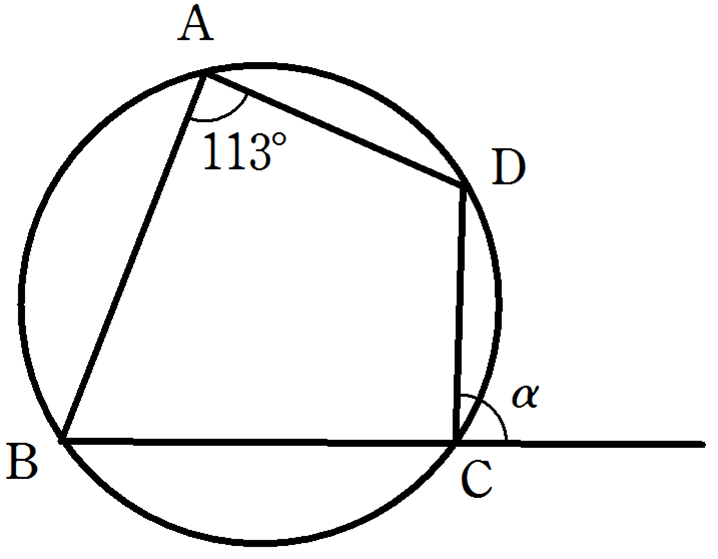
解答
四角形ABCDは円に内接しているので
\(\alpha = \angle\mathrm{BAD} = 113^{\circ}\)
よって
\(\color{red}{\alpha = 113^{\circ}}\)
①\(PA \cdot PB =PC \cdot PD\)
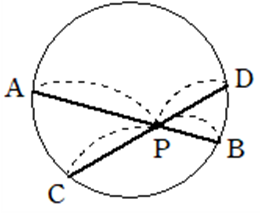
②\(PA \cdot PB =PC \cdot PD\)
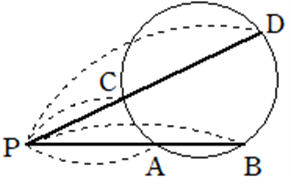
③\(PA \cdot PB =PT^2\)
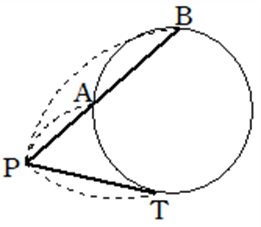
例題
次の図において、CPの長さを求めよ。

解答
方べきの定理より
\(PA \cdot PB =PC \cdot PD\) より
\(4 \times 2 = PC \times 3\)
\(CP = \displaystyle\frac{8}{3}\)
図のような△ABC において
\(\displaystyle\frac{RB}{AR} \cdot \displaystyle\frac{PC}{BP} \cdot \displaystyle\frac{QA}{CQ} = 1\)
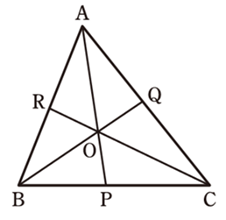
例題
次の図の△ABC において, \(3\) 点\(P, Q, R\) は
それぞれ辺\(BC, CA, AB\)上の点です。
\(3\) つの線分\(AP, PQ, CR\) が1点\(O\) で交わるとき,
\(AR:RB\) を最も簡単な整数の比で表しなさい。
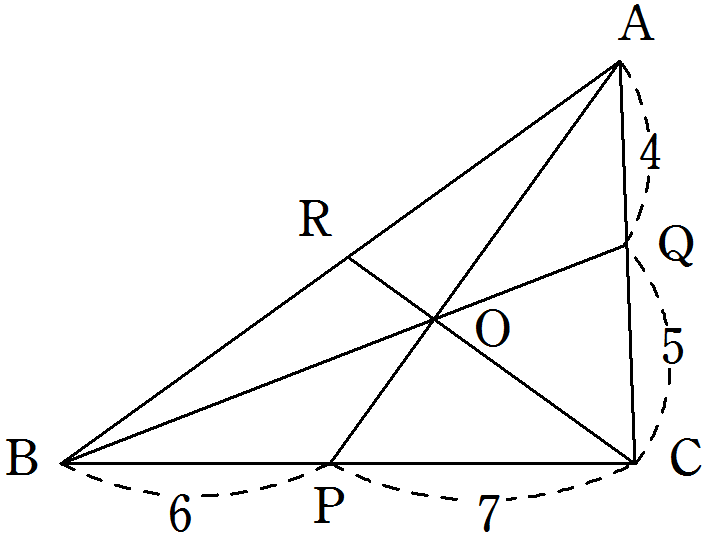
解答
△ABC においてチェバの定理より
\(\displaystyle\frac{RB}{AR} \times \displaystyle\frac{PC}{BP} \times \displaystyle\frac{QA}{CQ} =1 \)
\(\displaystyle\frac{RB}{AR} \times \displaystyle\frac{7}{6} \times \displaystyle\frac{4}{5} =1 \)
\(\displaystyle\frac{RB}{AR} = \displaystyle\frac{15}{14} \)
したがって、
\(\color{red}{AR : RB = 14 : 15}\)
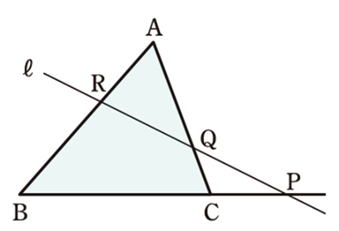
図のような△ABC と直線\(\ell\)において
\(\displaystyle\frac{RB}{AR} \cdot \displaystyle\frac{PC}{BP} \cdot \displaystyle\frac{QA}{CQ} = 1\)
例題
次の図の△ABC において, \(3\) 点\(P, Q, R\) は
それぞれ辺\(BC, CA, AB\)上の点です。
\(3\) つの線分\(AP, PQ, CR\) が1点\(O\) で交わるとき,
\(AO:OP\) を最も簡単な整数の比で表しなさい。

解答
三角形ABCと線分CRにおいて、メネラウスの定理より
\(\displaystyle\frac{QC}{AQ} \cdot \displaystyle\frac{BP}{CB} \cdot \displaystyle\frac{OA}{PO} = 1\) より
\(\displaystyle\frac{5}{4} \cdot \displaystyle\frac{6}{13} \cdot \displaystyle\frac{OA}{PO} = 1\) より
\(\displaystyle\frac{OA}{PO} = \displaystyle\frac{26}{15}\)
よって
AO:OP=26:15
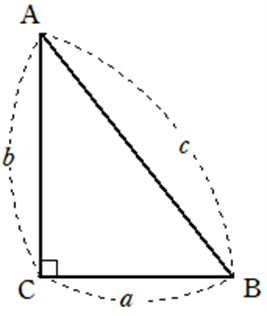
\(\angle C = 90^\circ\) の直角三角形ACBにおいて
\(a^2 + b^2 = c^2\)
例題
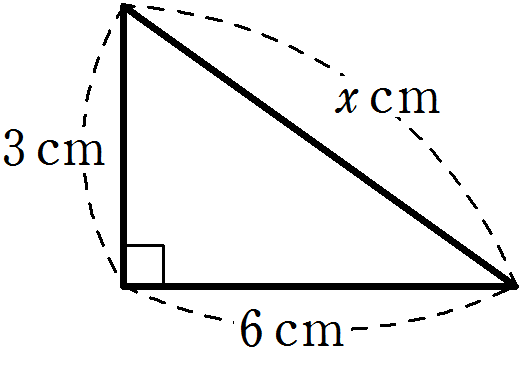
右の図の直角三角形において、\(x\) の値を求めなさい。
解答
三平方の定理より
\(x = \sqrt{3^2 + 6^2}\)
\(x = \sqrt{45}\)
\(\color{red}{x = 3\sqrt{5}}\)
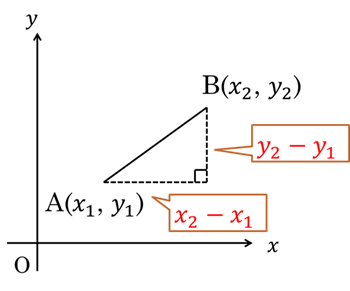
2点\(A(x_1, y_1)\), \(B(x_2, y_2)\) 間の距離\(d\) は
\(d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}\)
例題
2点\(A(2, 1), B(5, 3)\)の距離 AB を求めよ。
解答
AB \(= \sqrt{(5 – 2)^2 + (3 – 1)^2}\)
\(= \sqrt{9 + 4}\)
\(= \sqrt{13}\)
2.立体図形・空間図形
①角柱の体積
底面積が\(S\), 高さが\(h\) の角柱の体積\(V\) は
\(V = SH\)
※(角柱の体積)=(底面積)×(高さ)

②円柱の体積
底面の半径が \(r\)、 高さが \(h\) の円柱の体積\(V\)は
\(V = \pi r^2 h\)
※円柱の場合は底面積\(S = \pi r^2\)となる

例題
底面の半径が \(2\)、 高さが \(5\) の円柱の体積\(V\) を求めよ。
解答
\(V = \pi 2^2 \times 5 = 20\pi\)
①角錐の体積
底面積が\(S\), 高さが\(h\) の角柱の体積\(V\) は
\(V = \displaystyle\frac{1}{3}SH\)
※(角柱の体積)=\(\displaystyle\frac{1}{3}\)×(底面積)×(高さ)

②円錐の体積
底面の半径が \(r\)、 高さが \(h\) の円柱の体積\(V\)は
\(V = \displaystyle\frac{1}{3}\pi r^2 h\)
※円錐の場合は底面積\(S = \pi r^2\)となる

例題
底面の半径が \(2\)、 高さが \(6\) である円錐の体積\(V\) を求めよ。
解答
\(V = \displaystyle\frac{1}{3} \cdot \pi \cdot 2^2 \cdot 6 = 8\pi \)
底面の半径\(r\), 高さが\(h\) である円柱の側面積\(S\)は
\(S = 2 \pi r h\)

例題
底面の半径\(2\), 高さが\(5\) である円柱の側面積\(S\) を求めよ。
解答
\(S = 2 \cdot \pi \cdot 2 \cdot 5 = 20\pi\)
底面の半径\(r\), 母線の長さが\(l\) である円錐における側面積\(S\)は
\(S = \pi r l\)

例題
底面の半径\(2\), 母線の長さが\(5\) である円錐における側面積\(S\) を求めよ。
解答
\(S = \pi \cdot 2 \cdot 5 = 10\pi\)
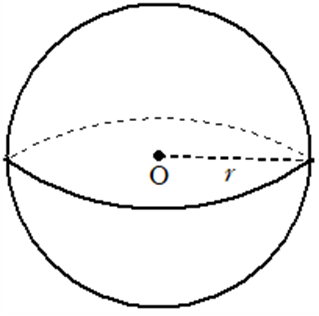
半径\(r\) の球において
①体積\(V = \displaystyle\frac{4}{3}\pi r^3\)
※「身(\(3\))の上に心配(\(4\pi\))ある(\(r\))ので参上(\(3乗\))」
と覚える
②表面積\(S = 4\pi r^2\)
※「心配(\(4\pi\))ある(\(r\))事情(\(2\)乗)」
と覚える
例題
半径が \(3\) である球について次の問いに答えよ。
(1)体積\(V\)
(2)表面積\(S\)
解答
(1)体積\(V = \displaystyle\frac{4}{3}\cdot \pi \cdot 3^3 = 36\pi\)
(2)表面積\(S = 4 \cdot \pi \cdot 3^2 = 36\pi\)
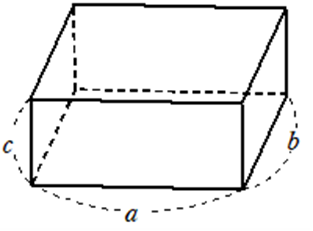
各辺の長さが\(a, b, c\)である直方体の対角線の長さ\(L\)
\(L = \sqrt{a^2+b^2+c^2}\)
例題
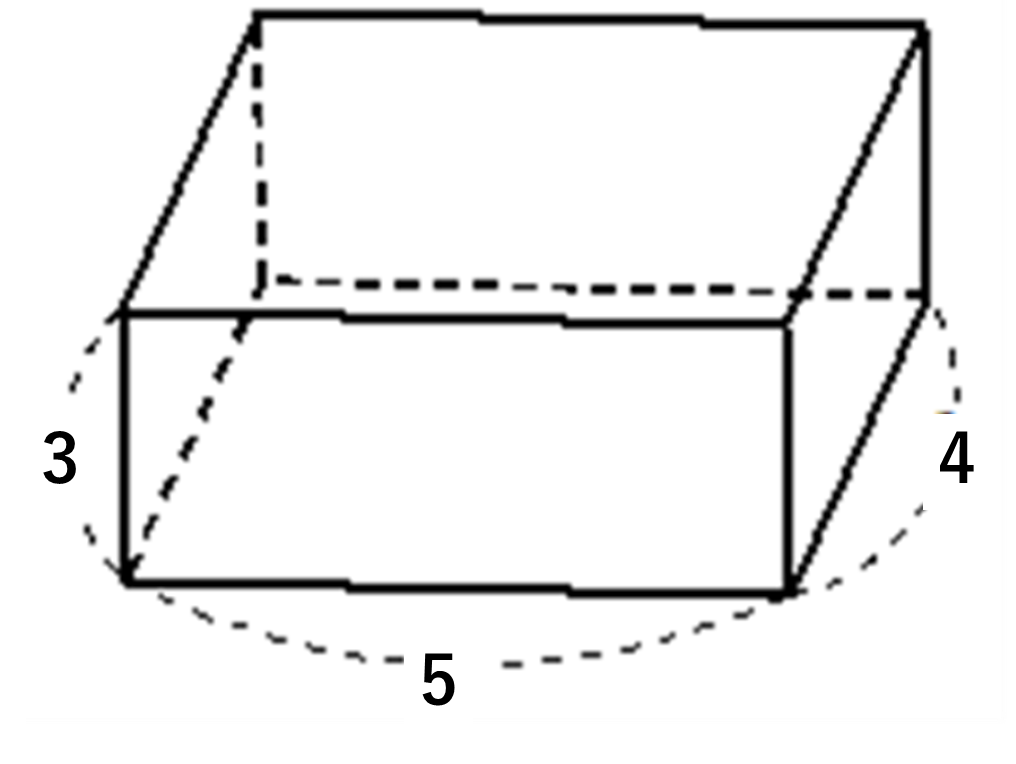
次のような直方体の対角線の長さ\(L\) を求めよ。
解答
\(L = \sqrt{3^2 + 4^2 + 5^2} = 5\sqrt{2}\)




コメント