ここでは、【数学II】「図形と方程式」でよく利用する公式(基礎知識)や例題を一覧にしてまとめています。
1.点の座標
2点\(A(x_1, y_1), B(x_2, y_2)\)の距離ABは
AB = \(\sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}\)
例題
2点\(A(2, 1), B(5, 3)\)の距離 AB を求めよ。
解答
AB \(= \sqrt{(5 – 2)^2 + (3 – 1)^2}\)
\(= \sqrt{9 + 4}\)
\(= \sqrt{13}\)
2点\(A(x_1, y_1), B(x_2, y_2)\)を結ぶ線分ABについて
①\(m : n\) に内分する点は
\(\left(\displaystyle\frac{nx_1 + mx_2}{m + n}, \displaystyle\frac{ny_1 + my_2}{m + n}\right)\)
②\(m : n\) に外分する点は
\(\left(\displaystyle\frac{-nx_1 + mx_2}{m – n}, \displaystyle\frac{-ny_1 + my_2}{m – n}\right)\)
③中点は
\(\left(\displaystyle\frac{x_1 + x_2}{2},\displaystyle\frac{y_1 + y_2}{2}\right)\)
例題
2点\(A(1, 3), B(3, 8)\)を結ぶ線分ABについて, 次の点の座標を求めよ。
① \(2 : 1\) に内分する点\(P\)
② \(2 : 1\) に外分する点\(Q\)
③ 中点\(M\)
解答
① \(P\left(\displaystyle\frac{1 \cdot 1 + 2 \cdot 3}{2 + 1}, \displaystyle\frac{1 \cdot 3 + 2 \cdot 8}{2 + 1}\right)\)
より
\(P\left(\displaystyle\frac{7}{3}, \displaystyle\frac{19}{3}\right)\)
② \(Q\left(\displaystyle\frac{-1 \cdot 1 + 2 \cdot 3}{2 – 1}, \displaystyle\frac{-1 \cdot 3 + 2 \cdot 8}{2 -1}\right)\)
より
\(Q\left(5 , 13\right)\)
③ \(M\left(\displaystyle\frac{1 + 3}{2},\displaystyle\frac{3 + 8}{2}\right)\)
より
\(M\left(2 , \displaystyle\frac{11}{2}\right)\)
3点\(A(x_1, y_1), B(x_2, y_2), C(x_3, y_3)\) を頂点とする△ABCの重心は
\(\left(\displaystyle\frac{x_1 + x_2 + x_3 }{3},\displaystyle\frac{y_1 + y_2 + y_3}{3}\right)\)
例題
3点\((A(2, 1), B(3, 5), C(-1, 2)\) を頂点とする△ABCの重心を求めよ。
解答
\(\left(\displaystyle\frac{2 + 3 – 1 }{3},\displaystyle\frac{1 + 5 + 2}{3}\right)\)
より
\(\left(\displaystyle\frac{4}{3},\displaystyle\frac{8}{3}\right)\)
2.直線の方程式
①点\((x_1, y_1)\) を通り,傾きが \(m\) の直線の方程式は
\(y – y_1 = m(x – x_1)\)
②点\((x_1, y_1)\) を通り,\(x\) 軸に垂直な直線の方程式は
\(x = x_1\)
例題
① 点\((1, 3)\) を通り,傾きが \(2\) の直線の方程式を求めよ。
② 点\((2, 4)\) を通り,\(x\) 軸に垂直な直線の方程式を求めよ。
解答
① \(y – 3 = 2(x – 1)\)
より
\(y = 2x +1\)
② 直線 \(x = 2\)
2点\((x_1, y_1), (x_2, y_2)\)を通る直線の方程式は
①\(x_1 \neq x_2\) のとき
\(y – y_1 = \displaystyle\frac{y_2 – y_1}{x_2 – x_1}(x – x_1)\)
②\(x_1 = x_2\) のとき
\(x = x_1\)
例題
① 2点\((1, 3), (3, 7)\)を通る直線の方程式を求めよ。
② 2点\((3, 1), (3, 5)\)を通る直線の方程式を求めよ。
解答
① \(y – 3 = \displaystyle\frac{7 – 3}{3 – 1}(x – 1)\)
より
\(y = 2x + 1\)
② 直線\(x = 3\)
3.2直線の平行・垂直
2直線\(y = m_1 x + n_1 , y = m_2 x + n_2\) について
①平行 ⇔ \(m_1 = m_2\)
②垂直 ⇔ \(m_1m_2 = -1\) ⇔ \(m_1 = -\displaystyle\frac{1}{m_2}\)
例題
① 2直線\(y = 2x + 1 , y = 2x + 3\) は平行と垂直のどちらか。
② 2直線\(y = -3x + 1 , y = \frac{1}{3}x + 2\) は平行と垂直のどちらか。
解答
① 2直線の傾きはともに \(2\) で等しいから
2直線は平行である。
② 2直線の傾きは \(-3\) と \(\displaystyle\frac{1}{3}\) であり,
\(-3 \times \displaystyle\frac{1}{3} = -1\) より
2直線は垂直である。
4.点と直線の距離
点\((x_1, y_1)\) と直線 \(ax + by + c = 0\) の距離\(d\) は
\(d = \displaystyle\frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}\)
※特に、原点\((0, 0)\) と直線 \(ax + by + c = 0\) の距離\(d\) は
\(d = \displaystyle\frac{|c|}{\sqrt{a^2 + b^2}}\)
例題
点\((2, 1)\) と直線 \(3x + 4y + 5 = 0\) の距離\(d\) を求めよ。
解答
\(d = \displaystyle\frac{|3 \cdot 2+ 4 \cdot 1 + 5|}{\sqrt{3^2 + 4^2}}\)
より
\(d = 3\)
5.円の方程式
中心\((a, b)\), 半径\(r\) の円の方程式は
\((x – a)^2 + (y – b)^2 = r^2\)
※特に、原点中心、半径\(r\) の円の方程式は
\(x^2 + y^2 = r^2\)
例題
中心\((2, 3)\), 半径\(5\) の円の方程式を求めよ。
解答
\((x – 2)^2 + (y – 3)^2 = 5^2\)
より
\((x – 2)^2 + (y – 3)^2 = 25\)
①中心と半径がわかる場合など
⇒ \((x – a)^2 + (y – b)^2 = r^2\)
②通る点がわかる場合など
⇒ \(x^2 + y^2 + lx +my + n = 0\)
例題
① 中心が\((2, 1)\) である円が点\((3, 2)\) を通るとき,この円の方程式を求めよ。
② 3点\((2, -2), (-1, 7), (6, 0)\) を通る円の方程式を求めよ。
解答
① 求める円の方程式を
\((x – 2)^2 + (y – 1)^2 = r^2\)
とおく。
これが,点\((3, 2)\) を通るから
\((3 – 2)^2 + (2 – 1)^2 = r^2\) より
\(r^2 = 2\)
したがって,
\((3 – 2)^2 + (2 – 1)^2 = 2\)
② 求める円の方程式を
\(x^2 + y^2 + lx +my + n = 0\)
とおく。
これが,3点\((2, -2), (-1, 7), (6, 0)\) を通るから
\(2^2 + (-2)^2 + l \cdot 2 +m \cdot (-2) + n = 0\) …(1)
\((-1)^2 + 7^2 + l \cdot (-1) +m \cdot 7 + n = 0\) …(2)
\(6^2 + 0^2 + l \cdot 6 +m \cdot 0 + n = 0\) …(3)
(1)〜(3)より,\(l =-4, m = -6, n = -12\) であるから
\(x^2 + y^2 – 4x – 6y – 12 = 0\)
6.円と直線の方程式
円の半径を\(r\) , 円の中心から直線までの距離を\(d\)とするとき
①円と直線が異なる2点で交わる ⇔ \(d < r\)
②円と直線が接する ⇔ \(d = r\)
③円と直線が交わらない ⇔ \(d > r\)
例題
円\(x^2 + y^2 = 1\) と直線\(y = x + k\) が異なる2点で交わるとき,定数\(k\) の値の範囲を求めよ。
解答
円の中心\((0, 0)\) と直線\(x -y + k = 0\)との距離\(d=\displaystyle\frac{|0 – 0 + k|}{\sqrt{1^2 + (-1)^2}}\)
であり,円\(x^2 + y^2 = 1\)の半径は\(1\) である。
したがって,円\(x^2 + y^2 = 1\) と直線\(x -y + k = 0\) が異なる2点で交わるとき,
\(\displaystyle\frac{|0 – 0 + k|}{\sqrt{1^2 + (-1)^2}} < 1\)
これを解くと \(-\sqrt{2} < k < \sqrt{2}\)
円 \(x^2 + y^2 = r^2\) 上の点\((x_1, y_2)\) における接線の方程式は
\(x_1 x + y_1 y = r^2\)
例題
円 \(x^2 + y^2 = 5\) 上の点\((2, 3)\) における接線の方程式を求めよ。
解答
\(2x + 3y = 5\)
7.2つの円の位置関係
2つの円\(C_1\), \(C_2\) の半径をそれぞれ\(r , r’\)\((r > r’)\) ,中心間の距離を\(d\)とすると
- 互いに外部にある ⇔ \(d > r + r’\)
- 外接する ⇔ \(d = r + r’\)
- 2点で交わる ⇔ \(r – r’ < d < r + r’\)
- 内接する ⇔ \(d = r – r’\)
- 一方が他方の内部 ⇔ \(d < r – r’\)
例題
中心が点\(3, 4\) である円\(C\) と円\(x^2 + y^2 = 1\) が外接するとき,円\(C\) の方程式を求めよ。
解答
円\(x^2 + y^2 = 1\) は原点中心,半径\(1\) の円である。
また求める円は中心が\((3, 4)\) であり,半径を\(r\) とすると,
中心間の距離\(d = \sqrt{3^2 +4^2} = 5\)
外接するとき,\(5 = 1 + r\) つまり,\(r =4\)
よって,中心が\((3, 4)\) であり,半径\(4\) の円は
\((x – 3)^2 + (y – 4)^2 = 16\)
8.軌跡を求める手順
- 条件を満たす点\(P\) の座標を\(x, y\)として、図示する
- \(x, y\) の関係式を求める
- 逆に,②で求めた関係式(図形)上のすべての点\(P(x, y)\) が条件を満たすことを確かめる
例題
2点\(A(2, 0), B(-3, 0)\) からの距離の比が\(2 : 3\) である点\(P\) の軌跡を求めよ。
解答
点\(P\) の座標を\(x, y\) とする。
\(P\) に関する条件は \(AP : BP = 2 : 3\) であるから
\(3AP = 2 BP\) すなわち
\(9AP^2 = 4 BP^2\)
\(9\{(x- 2)^2 + y^2\} = 4\{(x + 3)^2 + y^2\}\)
より
\(x^2 + y^2 -12x = 0
すなわち
\((x – 6)^2 + y^2 = 36\)
よって,点\(P\) は円\((x – 6)^2 + y^2 =36\) 上にある。
逆に,この円上のすべての点\(P(x, y)\) は,条件を満たす。
したがって,求める軌跡は,点\((6, 0)\) を中心とする半径\(6\) の円である。
9.不等式の表す領域
直線 \(y = ax + b\) について、
① 不等式 \(y > ax + b\)の表す領域は直線\(y = ax + b\)の上側の部分。ただし、境界線を含まない。
② 不等式 \(y < ax + b\)の表す領域は直線\(y = ax + b\)の下側の部分。ただし、境界線を含まない。
③ 不等式 \(y \geq ax + b\)の表す領域は直線\(y = ax + b\)の上側の部分。ただし、境界線を含む。
④ 不等式 \(y \leq ax + b\)の表す領域は直線\(y = ax + b\)の下側の部分。ただし、境界線を含む。
曲線\(y = f(x)\)について
①’ 不等式\(y > f(x)\)の表す領域は、曲線\(y = f(x)\)の上側の部分。ただし、境界線を含まない。
②’ 不等式\(y < f(x)\)の表す領域は、曲線\(y = f(x)\)の下側の部分。ただし、境界線を含まない。
曲線\(x = g(y)\)について、
③’ 不等式 \(x < g(y)\)の表す領域は、曲線の左側の部分。ただし、境界線を含まない。
④’ 不等式 \(x > g(y)\)の表す領域は、曲線の右側の部分。ただし、境界線を含まない。
例題
\( y > -x + 2 \) の表す領域を答えよ。
解答
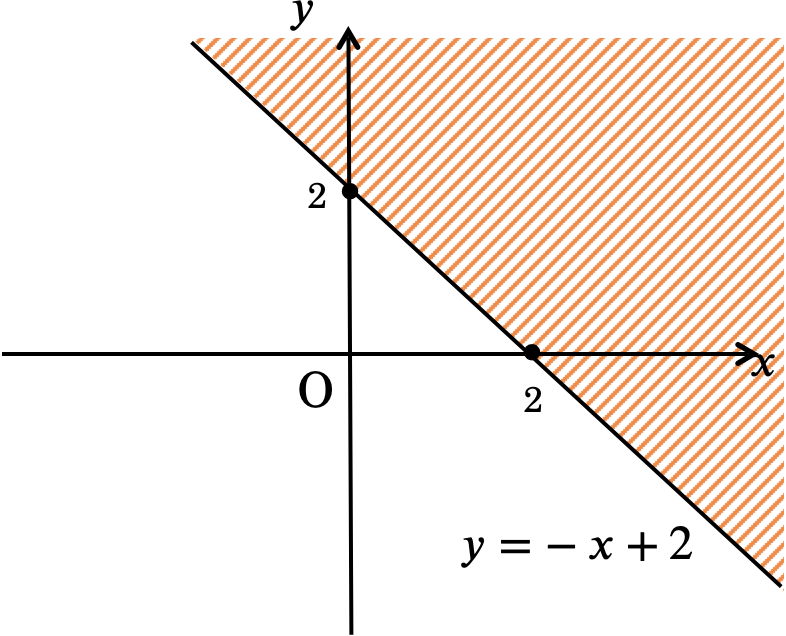
図の斜線部分。ただし,境界線は含まない。
円 \(C : (x – a)^2 + (y – b)^2 = r^2\) について、
① 不等式 \(C : (x – a)^2 + (y – b)^2 < r^2\)の表す領域は円\(C\) の内部。ただし、境界線を含まない。
② 不等式 \(C : (x – a)^2 + (y – b)^2 > r^2\)の表す領域は円\(C\) の外部。ただし、境界線を含まない。
例題
\((x – 1)^2 + (y -2)^2 < 4\) の表す領域を答えよ。
解答
中心\((1, 2)\), 半径\(2\) の円の内部より
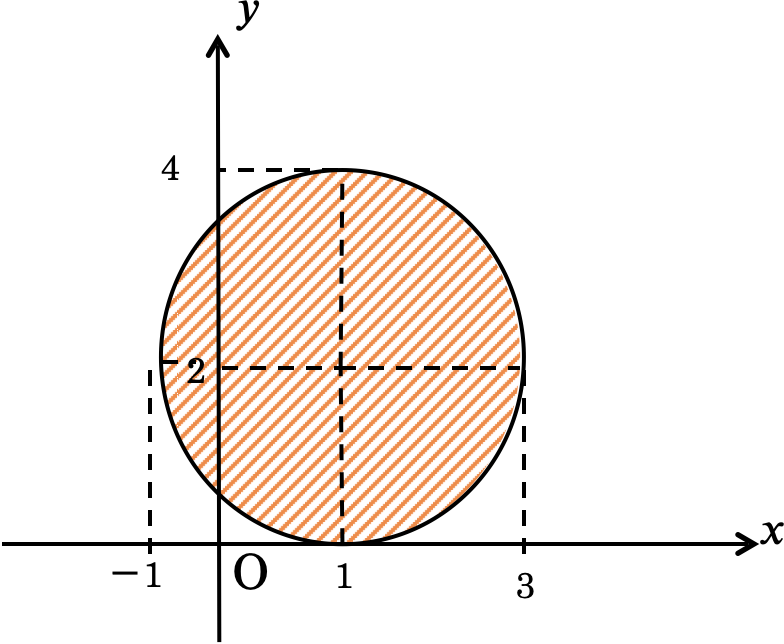
図の斜線部分。ただし,境界線は含まない。





コメント