【数学Ⅲ】公式一覧～関数・数列の極限・関数の極限・微分法・積分法～

①　定義域は\(x \neq p\), 値域は\(y \neq q\)

②　漸近線は\(x = 0\) (\(y\) 軸), \(y = 0\) (\(x\) 軸)

③ グラフの存在範囲は　
\(k > 0\) のとき第1象限、第3象限
\(k < 0\) のとき第2象限、第4象限

④　グラフは原点対称

⑤　概形は直角双曲線（漸近線が直交している）

①　\(y = \displaystyle\frac{k}{x}\) を \(x\) 軸方向\(p\) , \(y\) 軸方向\(q\) だけ平行移動したグラフ

②　漸近線は \(x = p , y = q\)

③　定義域は \(x \neq p\), 値域は\(y \neq q\)

\( y = \displaystyle\frac{ax + b}{cx + d}\) のグラフ 　⇒　　\( y = \displaystyle\frac{k}{x – p} + q\) に変形する

\(a > 0\) のとき

①　定義域：\(x \geq 0\), 値域：\(y \geq 0\)

②　グラフは単調増加

③　概形は\(y^2 = x\) の上側\(x \geq 0, y \geq 0\) の部分

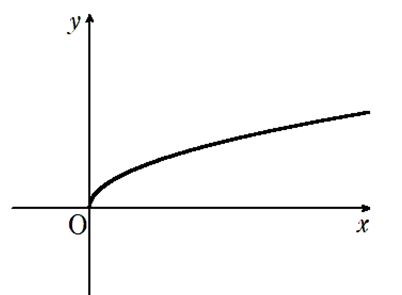
無理関数\(y = \sqrt{a(x – p)}\) のグラフは

①　\(y = \sqrt{ax}\)のグラフを\(x\) 軸方向に\(p\) だけ平行移動したグラフ

②　定義域と値域は
・\(a > 0\) のとき、定義域：\(x \geq p\) , 値域：\(y \geq 0\)
・\(a < 0\) のとき、定義域：\(x \leq p\) , 値域：\(y \geq 0\)

関数\(f(x)\) が逆関数 \(f^{-1}(x)\) をもつとき

①　\(b = f(a) \iff a = f^{-1}(b)\)

②　\(f(x)\) と \(f^{-1}(x)\) では、定義域と値域が入れ替わる

③　\(y = f(x)\) のグラフと\(y = f^{-1}(x)\) のグラフは直線\(y = x\) に関して対称

\(f(x)\) の値域が \(g(x)\) の定義域に含まれているとき

\((g \circ f) (x) = g(f(x))\)

①　一般に\((g \circ f) (x)\) と \((f \circ g) (x)\) は一致しない。

②　\(f(x)\) の逆関数が \(g(x)\) のとき,それぞれの定義域で
\((f \circ g) (x) = x\) , \((g \circ f) (x) = x\)

\(\lim\limits_{n \to \infty} a_n = \alpha\), \(\lim\limits_{n \to \infty} b_n = \beta\) とする。

①　\(\lim\limits_{n \to \infty} (k a_n + l b_n) = k\alpha + l\beta\) \((k, l は定数) \)

②　\(\lim\limits_{n \to \infty} a_n b_n = \alpha\beta\)

③　\(\lim\limits_{n \to \infty} \displaystyle\frac{a_n}{b_n} = \displaystyle\frac{\alpha}{\beta} (\beta \neq 0)\)

④　すべての \(n\) について \(a_n \leq b_n\) \(\Rightarrow\) \(\alpha \leq \beta\)

⑤　すべての \(n\) について \(a_n \leq c_n \leq b_n\) かつ \(\alpha = \beta\) \(\Rightarrow\) \(\lim\limits_{n \to \infty} c_n = \alpha\)

\(\lim\limits_{n \to \infty} a_n = \alpha\) \(\iff\) \(\lim\limits_{n \to \infty}(a_n – \alpha) = 0 \)\(\iff\) \(\lim\limits_{n \to \infty}| a_n – \alpha | = 0\)

無限等比数列\(\{ r^n \}\)は

\(r > 1\) のとき　\(\lim\limits_{n \to \infty} r^n = \infty\) 　← 発散する

\(r = 1\) のとき　\(\lim\limits_{n \to \infty} r^n = 1\)　← 収束する

\(|r| < 1\) のとき　\(\lim\limits_{n \to \infty} r^n = 0\) 　← 収束する

\(r \leq -1\) のとき　振動する　← 極限はない

したがって

数列\(\{ r^n \} \) が収束　\(\iff\) \(-1 < r \leq 1\)

無限級数\(\displaystyle\sum_{n = 1}^{\infty} a_n\) は

第\(n\) 項までの部分和 \(S_n = a_1 + a_2 + a_3 + \cdots\cdots + a_n\) が\(S\) に収束するとき収束し,　その和は\( S\) である。

無限等比級数 \(\displaystyle\sum_{n = 1}^{\infty} a_n\) は

\(| r | < 1\) のとき　収束し, 和は\(\displaystyle\frac{a}{1-r}\)
\(| r | \geq 1\) のとき　発散する

\(\displaystyle\sum_{n = 1}^{\infty} a_n = S\), \(\displaystyle\sum_{n = 1}^{\infty} b_n = T\) のとき、←収束する必要がある

\(\displaystyle\sum_{n = 1}^{\infty} (ka_n + lb_n ) = kS +lT\) (\(k, l\) は定数)

①　\(\displaystyle\sum_{n = 1}^{\infty} a_n\) が収束する　\(\Rightarrow\) \(\lim\limits_{n \to \infty} a_n = 0\)

②　\(\{a_n\}\) が \(0\) に収束しない　\(\Rightarrow\) \(\displaystyle\sum_{n = 1}^{\infty} a_n\) は発散する

\(\lim\limits_{x \to a} f(x) = \alpha\), \(\lim\limits_{x \to a} g(x) = \beta\) とする。

①　\(\lim\limits_{x \to a} \{k f(x) + l g(x)\} = k\alpha + l\beta\) \((k, l は定数) \)

②　\(\lim\limits_{x \to a} f(x) g(x) = \alpha\beta\)

③　\(\lim\limits_{x \to a} \displaystyle\frac{f(x)}{g(x)} = \displaystyle\frac{\alpha}{\beta} (\beta \neq 0)\)

④　\(x\) が \(a\) に近いとき, 常に \(f(x) \leq g(x)\) \(\Rightarrow\) \(\alpha \leq \beta\)

⑤ \(x\) が \(a\) に近いとき, 常に \(f(x) \leq h(x) \leq g(x)\) かつ \(\alpha = \beta\) \(\Rightarrow\) \(\lim\limits_{x \to a} h(x) = \alpha\)

\(\lim\limits_{x \to a} f(x) = \alpha\) \(\iff\) \(\lim\limits_{x \to a} |f(x) – \alpha| = 0 \)
特に \(\lim\limits_{x \to a} f(x) = 0\) \(\iff\) \(\lim\limits_{x \to a} |f(x)| = 0\)

\(\lim\limits_{x \to a + 0} f(x) = \lim\limits_{x \to a – 0} f(x) = \alpha\) \(\iff\) \(\lim\limits_{x \to a } f(x) = \alpha\)

\(\alpha > 0\) のとき　\(\lim\limits_{x \to \infty} x^\alpha = \infty\)

\(\alpha < 0\) のとき　\(\lim\limits_{x \to \infty} x^\alpha = 0\)

\( \alpha >1\) のとき　\(\lim\limits_{x \to \infty} a^x = \infty\),\(\lim\limits_{x \to -\infty} a^x = 0\)

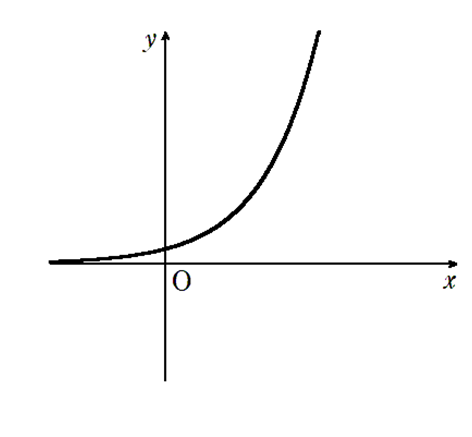
\( 0 < \alpha < 1\) のとき　\(\lim\limits_{x \to \infty} a^x = 0\),\(\lim\limits_{x \to -\infty} a^x = \infty\)

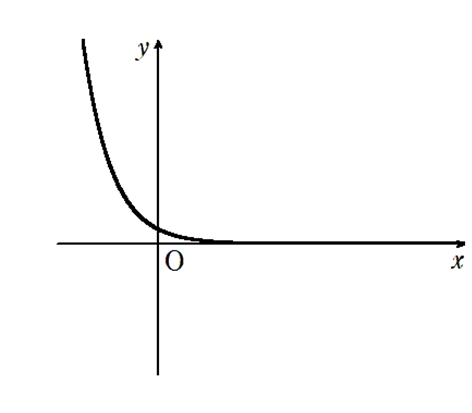
\( \alpha >1\) のとき　\(\lim\limits_{x \to \infty} \log_a x = \infty\),\(\lim\limits_{x \to +0} \log_a x = -\infty\)

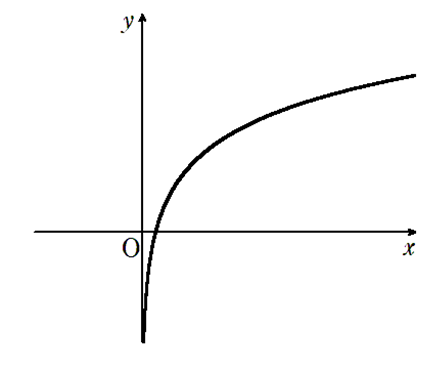
\( 0 < \alpha < 1\) のとき　\(\lim\limits_{x \to \infty} \log_a x = -\infty\),\(\lim\limits_{x \to +0} \log_a x = \infty\)

① \(\lim\limits_{x \to 0} \displaystyle\frac{\sin x}{x} = 1\)

② \(\lim\limits_{x \to 0} \displaystyle\frac{x}{\sin x} = 1\)

定義域の \(x\) の値 \(a\) に対して, \(\lim\limits_{x \to a} f(x) = f(a)\) のとき, \(f(x)\) は \(x = a\) で連続

閉区間 \([ a, b]\) で連続な関数 \(f(x)\) について

・\(f(x)\) はこの区間で\(f(a)\) と \(f(b)\) の間の任意の値をとる。

・\(f(a)\) と \(f(b)\) が異符号ならば, 方程式 \(f(x) = 0 \) は \(a < x < b\) の範囲に少なくとも1つの実数解をもつ。

\( f'(a) = \lim\limits_{h \to 0} \displaystyle\frac{f(a + h) – f(a)}{h} = \lim\limits_{x \to a} \displaystyle\frac{f(x) – f(a)}{x – a}\)

関数 \(f(x)\) について

①　\(f'(a)\) が存在するとき, \(x = a\) で微分可能

②　\(x = a\) で微分可能　\(\Rightarrow\) \(x = a\) で連続

③　\(x = a\) で連続であっても, \(x = a\) で微分可能とは限らない

\( f'(x) = \lim\limits_{h \to 0} \displaystyle\frac{f(x + h) – f(x)}{h}\)

\(k , l\) は定数とする。

①　\(\{k f(x) + l g(x)\}’ = k f'(x) + l g'(x)\)

②　\(\{f(x)g(x)\}’ = f'(x)g(x) + f(x)g'(x)\)　←積の微分法

③　\(\left\{\displaystyle\frac{f(x)}{g(x)}\right\}’ = \displaystyle\frac{f'(x)g(x) – f(x)g'(x)}{\{ g(x) \}^2}\)　←商の微分法

\(y = f(u), u = g(x)\) のとき

\(\displaystyle\frac{dy}{dx} = \displaystyle\frac{dy}{du} \cdot \displaystyle\frac{du}{dx}\)

\(\displaystyle\frac{dy}{dx} = \displaystyle\frac{1}{\displaystyle\frac{dx}{dy}}\)

①　\((c)’ = 0\) (\(c\) は定数)

②　\((x^\alpha)’ = \alpha x^{\alpha – 1}\) (\(\alpha\) は実数)

①　\((\sin x)’ = \cos x\)

②　\((\cos x)’ = – \sin x\)

③　\((\tan x)’ = \displaystyle\frac{1}{\cos^{2}x } \)

\(a > 0, a \neq 1\) のとき

①　\((\log |x|)’ = \displaystyle\frac{1}{x}\)

②　\((\log_a |x|)’ = \displaystyle\frac{1}{x\log a}\)

\(a > 0, a \neq 1\) のとき

①　\((e^x)’ = e^x\)

②　\((a^x)’ = a^x \log a\)

※\(e = \lim\limits_{k \to 0}(1 + k)^{\frac{1}{k}} = 2.71828\cdots\cdots\)

関数\(y = f(x)\) を\(n\) 回微分して得られる関数を

\(y^{(n)}\), \(f^{(n)}(x)\), \(\displaystyle\frac{d^n y}{dx^n}\), \(\displaystyle\frac{d^n}{dx^n}f(x)\) 　

などで表す。

方程式\(F(x, y) = 0\) について、\(y\) を \(x\) の関数と考え、両辺を\(x\) で微分すると,

\(\displaystyle\frac{d}{dx}f(y) = \displaystyle\frac{d}{dy}f(y) \cdot \displaystyle\frac{dy}{dx}\)

\(x = f(t), y = g(t)\) のとき

\(\displaystyle\frac{dy}{dx} = \displaystyle\frac{\displaystyle\frac{dy}{dt}}{\displaystyle\frac{dx}{dt}} = \displaystyle\frac{g'(t)}{f'(t)}\)

曲線 \(y = f(x)\) 上の点 \(A(a, f(a))\) において

①　接線の方程式　→　\(y – f(a) = f^{\prime}(a)(x – a)\)

②　法線の方程式　→　\(y – f(a) = – \displaystyle\frac{1}{f'(a)} (x – a)\) (ただし、\(f^{\prime}(a) = 0\))

関数 \(f(x)\) が閉区間\([a, b]\) で連続, 開区間\((a, b)\) で微分可能ならば,

\(\displaystyle\frac{f(b) – f(a)}{b – a} = f'(c)\), \((a < c < b)\)

を満たす実数 \(c\) が存在する。

曲線\(y= f(x)\) は

①　\(f^{\prime\prime}(x) > 0\) である区間では 下に凸

②　\(f^{\prime\prime}(x) < 0\) である区間では 上に凸

曲線 \(y = f(x)\) について

①　\(f^{\prime\prime}(a) = 0 \) のとき, \(x = a \) の前後で \(f^{\prime\prime}(x)\) の符号が変わる
\(\Rightarrow\) 　 点\((a, f(a))\) は曲線の変曲点

②　\(f^{\prime\prime}(a)\) が存在し、点 \((a, f(a))\) が曲線の変曲点　
\(\Rightarrow\) \(f^{\prime\prime}(a) = 0\)

\( x = a\) を含むある区間で \(f^{\prime\prime}(x)\) は連続であるとする。

①　\(f^{\prime}(a) = 0\) かつ \(f^{\prime\prime}(a) < 0\) \(\Rightarrow\) \(f(a)\) は極大値

②　\(f^{\prime}(a) = 0\) かつ \(f^{\prime\prime}(a) > 0\) \(\Rightarrow\) \(f(a)\) は極小値

数直線上を運動する点\(P\) の時刻\(t\) における座標を \(x = f(t)\) とすると,点\(P\) は時刻\(t\) において

①　速度\(v = \displaystyle\frac{dx}{dt} = f^{\prime}(t)\)

②　加速度\(\alpha = \displaystyle\frac{dv}{dt} = \displaystyle\frac{d^2v}{dt^2} = f^{\prime\prime}(t)\)

座標平面上を運動する点\(P\) の時刻\(t\) における座標\((x , y)\) が \(t\) の関数であるとき,点\(P\) の時刻\(t\) における速度\(\overrightarrow{ v }\), 速さ \(| \overrightarrow{v} |\), 加速度\(\overrightarrow{ \alpha }\), 加速度の大きさ \(| \overrightarrow{\alpha} |\) は

①　速度\(\overrightarrow{ v } = \left( \displaystyle\frac{dx}{dt}, \displaystyle\frac{dy}{dt} \right)\)

②　速さ \(| \overrightarrow{v} | = \sqrt{\left( \displaystyle\frac{dx}{dt} \right)^2 + \left( \displaystyle\frac{dy}{dt} \right)^2}\)

③　加速度\(\overrightarrow{ \alpha } = \left( \displaystyle\frac{d^2x}{dt^2}, \displaystyle\frac{d^2y}{dt^2} \right)\)

④　加速度の大きさ \(| \overrightarrow{\alpha} | = \sqrt{\left( \displaystyle\frac{d^2x}{dt^2} \right)^2 + \left( \displaystyle\frac{d^2y}{dt^2} \right)^2} \)

①　\(| h |\) が十分小さいとき　\(f(a + h) \) は\( f(a) + f^{\prime}(a)h\) にほぼ等しい

②　\(| x |\) が十分小さいとき　\(f(x)\)は\( f(0) + f^{\prime\prime}(0)x\) にほぼ等しい

①　\(\displaystyle\int x^\alpha dx = \displaystyle\frac{1}{\alpha + 1} x^{\alpha + 1} + C\) (\(\alpha \neq -1\))

②　\(\displaystyle\int \displaystyle\frac{1}{x} dx = \log |x| + C\)

①　\(\displaystyle\int \sin x dx = – \cos x + C\)

②　\(\displaystyle\int \cos x dx = \sin x + C\)

③　\(\displaystyle\int \displaystyle\frac{dx}{\cos^2 x} = \tan x + C\)

④　\(\displaystyle\int \displaystyle\frac{dx}{\sin^2 x} = -\displaystyle\frac{1}{\tan x} + C\)

①　\(\displaystyle\int e^x dx = e^x + C\)

②　\(\displaystyle\int a^x dx = \displaystyle\frac{a^x}{\log a} + C\)

①　\(\displaystyle\int f(x) dx = \int f(g(t)) g'(t) dt \) \((x = g(t))\)

②　\(\displaystyle\int f(g(x)) g'(x) dx = \int f(u) du \) \( (g(x) = u )\)

\( \displaystyle\int f(x)g'(x) dx = f(x)g(x) – \int f'(x)g(x) dx\)

①　\(f(x) \) が偶関数のとき　\(\displaystyle\int_{-a}^{a} f(x) dx = 2\int_{0}^{a} f(x) dx\)

②　\(f(x) \) が奇関数のとき　\(\displaystyle\int_{-a}^{a} f(x) dx = 0 \)

\(x = g(t) \) は \(\alpha \leq t \leq \beta\) で微分可能,　\(a = g(\alpha), b = g(\beta)\) とする。

\(\displaystyle\int_{a}^{b} f(x) dx = \displaystyle\int_{\alpha}^{\beta} f(g(t)) g'(t) dt\)

\(\displaystyle\int_{a}^{b} f(x)g'(x) dx = \left[ f(x)g(x) \right]_{a}^{b} – \displaystyle\int_{a}^{b} f'(x)g(x) dx \)

\(a\) が定数のとき

\(\displaystyle\frac{d}{dx} \displaystyle\int_{a}^{x} f(t) dt = f(x)\)

①　\(\int_{a}^{b} f(x) dx = \displaystyle \lim_{ n \to \infty }\displaystyle\sum_{k = 0}^{n – 1} f(x_k) \Delta x = \displaystyle \lim_{ n \to \infty }\displaystyle\sum_{k = 1}^{n} f(x_k) \Delta x\)

ここで、　\(\Delta x = \displaystyle\frac{b – a}{n}\) , \(x_k = a + k\Delta x\)

②　\(\displaystyle \lim_{ n \to \infty }\displaystyle\frac{1}{n} \displaystyle\sum_{k = 0}^{n – 1} f(\displaystyle\frac{k}{n}) = \displaystyle \lim_{ n \to \infty }\displaystyle\frac{1}{n} \displaystyle\sum_{k = 1}^{n} f(\displaystyle\frac{k}{n}) = \displaystyle\int_{0}^{1} f(x) dx\)

区間 \(\left[ a, b \right] \) で \(f(x) \geq g(x)\) ならば

\(\displaystyle\int_{a}^{b} f(x) dx \geq \displaystyle\int_{a}^{b} g(x) dx\)

等号は,常に \(f(x) = g(x)\) であるときに限って成り立つ。

区間 \(a\leq x \leq b\) において

\(f(x) \geq 0\) のとき　\(S = \displaystyle\int_{a}^{b}f(x)dx\)

\(f(x) \leq 0\) のとき　\(S = \displaystyle\int_{a}^{b}\{-f(x)\}dx\)

区間 \(a\leq x \leq b\)で常に \(f(x) \geq g(x)\) のとき

\(S = \displaystyle\int_{a}^{b}\{f(x) – g(x) \}dx\)

区間 \(c\leq y \leq d\) において常に \(g(y) \geq 0\) のとき　\(S = \displaystyle\int_{c}^{d}g(y)dy\)

区間 \(a\leq x \leq b\) において

\(V = \displaystyle\int_{a}^{b}S(x)dx\)

①　曲線 \(y = f(x)\) と\(x\) 軸の間の部分 \(( a \leq x \leq b )\) を\(x\) 軸の周りに１回転させてできる回転体の体積は

\(V = \pi \displaystyle\int_{a}^{b} \{f (x)\}^2 dx = \pi \displaystyle\int_{a}^{b} y^2 dx \)

②　曲線 \(x = g(y)\) と \(y\) 軸の間の部分 \((c \leq y \leq d )\) を \(y\) 軸の周りに１回転させてできる回転体の体積は

\(V = \pi \displaystyle\int_{c}^{d} \{g (y)\}^2 dy = \pi \displaystyle\int_{c}^{d} x^2 dy \)

\(L = \displaystyle\int_{\alpha}^{\beta} \sqrt{\left( \displaystyle\frac{dx}{dt} \right)^2 + \left( \displaystyle\frac{dy}{dt} \right)^2} dt \)

\(L = \displaystyle\int_{a}^{b} \sqrt{ 1 + \left( \displaystyle\frac{dy}{dx} \right)^2} dx \)

数直線上を運動する点\(P\) の速度を \(v = f(t)\) とし, \(t = a\) のときの \(P\) の座標を\(k\) とする。

①　\(t = b\) における\(P\) の座標 \(x\) は
\(x = k + \displaystyle\int_{a}^{b} f(t) dt\)

②　\(t = a\) から\(t = b\) までの\(P\) の位置の変化量 \(s\) は
\(s = \displaystyle\int_{a}^{b} f(t) dt\)

③　\(t = a\) から\(t = b\) までの\(P\) の道のり \(l\) は
\(l = \displaystyle\int_{a}^{b} |f(t)| dt\)