記事内に商品プロモーションを含む場合があります
平面上で、図形上の各点を直線や点に関してそれと対称な位置に移すことを,対称移動といいます。
この記事では2次関数に関する対称移動の問題の解き方について解説していきます。
2次関数の対称移動の解き方
点の対称移動
まず、点に関する対称移動をみていきましょう。
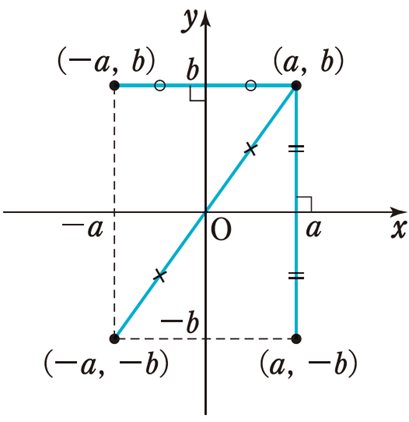
点\((a, b)\) を, \(x\) 軸, \(y\) 軸, 原点に関して対称移動した点はそれぞれ次のようになります。
点\((a, b)\) について
・\(x\) 軸に関する対称移動:\((a, -b)\)
⇒ \(\color{red}{y}\) 座標を変える(\(\color{red}{x}\) 軸固定)
・\(y\) 軸に関する対称移動:\((-a, b)\)
⇒ \(\color{red}{x}\) 座標を変える(\(\color{red}{y}\) 軸固定)
・原点に関する対称移動:\((-a, -b)\)
⇒ \(\color{red}{x, y}\) 座標を両方変える(固定なし)
基本的に平行移動と同様に\(x\) や \(y\) をおき換えればOKです。
対称移動はどちらをおき換えればいいか迷うことが多いですが、例えば\(x\) 軸対称であれば
「\(x\)軸を基準に折り返した点」
になるため、「\(x\)軸を固定する(変えない)」と覚えておくとよいでしょう。
放物線の対称移動
続いて、放物線の対称移動について考えていきましょう。
放物線\(F\)上の点\(P(x, y)\) を \(x\)軸対称した点\(Q\) は
\(Q(x, -y)\)
と表せるので、放物線\(F\) を\(x\) 軸対称した\(G\)の方程式は
\(y\) を \(-y\) におき換えた式になります。
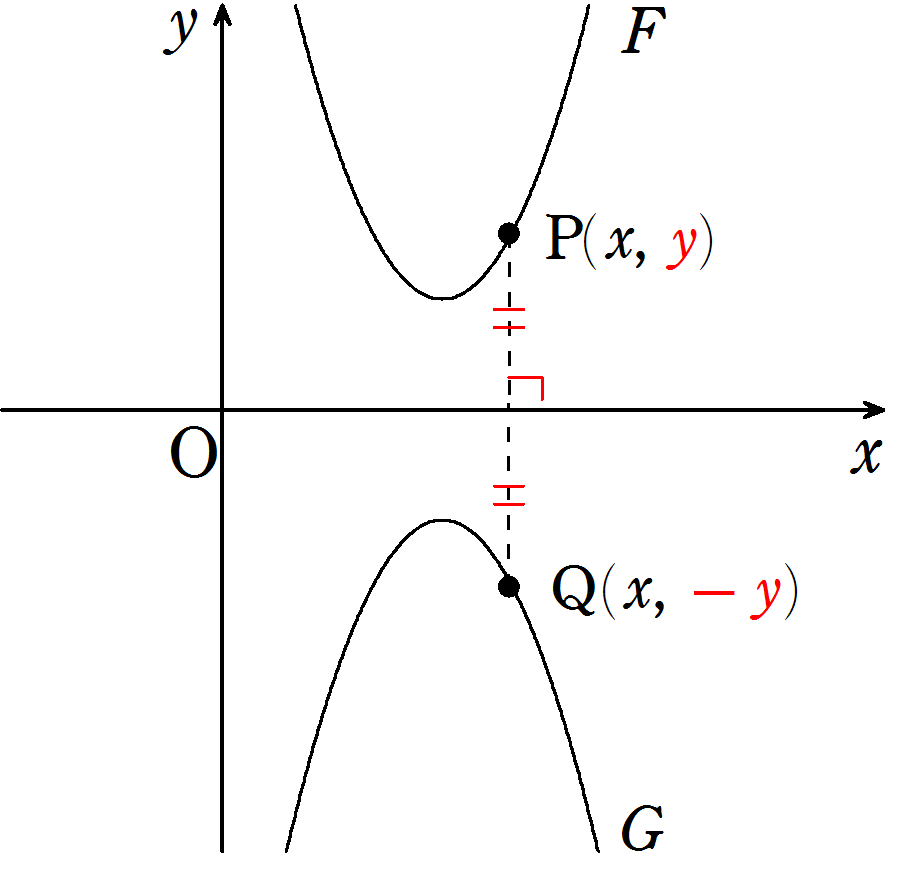
したがって、一般的に次のことが成り立ちます。
放物線 \(y = ax^2 + bx + c\) について
・\(x\) 軸対称:\(-y = ax^2 + bx + c\)
⇒ \(\color{red}{y}\) 座標を変える\(\color{red}{x}\) 軸固定)
・\(y\) 軸対称:\(y = a(-x)^2 + b(-x) + c\)
⇒ \(\color{red}{x}\) 座標を変える\(\color{red}{y}\) 軸固定)
・原点対称:\(-y = a(-x)^2 + b(-x) + c\)
⇒ \(\color{red}{x, y}\) 座標を両方変える(固定なし)
例題 放物線 \(y = 2x^2 – 3x + 5\) を, \(x\) 軸 , \(y\) 軸, 原点に関して,それぞれ対称移動して得られる放物線の方程式を求めよ。
放物線 \(y = 2x^2 – 3x + 5\) について
【\(x\) 軸対称】
\(-y = 2x^2 – 3x + 5\) より \(y = -2x^2 + 3x – 5\)
⇒ \(\color{red}{y}\) 座標を変える(\(\color{red}{x}\) 軸固定)
【\(y\) 軸対称】
\(y = 2(-x)^2 – 3(-x) + 5\) より \(y = 2x^2 + 3x + 5\)
⇒ \(\color{red}{x}\) 座標を変える(\(\color{red}{y}\) 軸固定)
【原点対称】
\(-y = 2(-x)^2 – 3(-x) + 5\) より \(y =- 2x^2 – 3x – 5\)
⇒ \(\color{red}{x, y}\) 座標を両方変える(固定なし)




コメント