1.2次関数のグラフ
頂点:点\((p, q)\)
軸:直線\(x=p\)
※\(y=ax^2\) のグラフを
\(x\)軸方向に\(p\)
\(y\)軸方向に\(q\)
だけ平行移動した放物線を表す。
例題
次の2次関数の頂点と軸を求めよ。
①\(y=2(x-2)^2+3\)
②\(y=(x+3)^2-1\)
③\(y=-(x-3)^2\)
④\(y=x^2+4\)
解答
①頂点:\((2, 3)\), 軸:直線\(x=2\)
②頂点:\((-3, -1)\), 軸:直線\(x=-3\)
③頂点:\((3, 0)\), 軸:直線\(x=3\)
④頂点:\((0, 4)\), 軸:直線\(x=0\)(\(y\)軸)
\(ax^2+bx+c\)の形を\(a(x-p)^2+q\)に変形することを平方完成という。
\(x^2-2px=(x-p)^2-p^2\)
例題
次の2次式を平方完成せよ。
①\(x^2-4x+2\)
②\(x^2+3x+2\)
③\(2x^2+4x+1\)
解答
①\(x^2-4x+2\)
\(=(x-2)^2-2^2+2\)
\(=(x-2)^2-2\)
②\(x^2+3x+2\)
\(=(x+\frac{3}{2})^2-(\frac{3}{2})^2+2\)
\(=(x+\frac{3}{2})^2-\frac{1}{4}\)
③\(2x^2+4x+1\)
\(=2(x^2+2x)+1\)
\(=2\{(x+1)^2-1\}+1\)
\(=2(x+1)^2-2+1\)
\(=2(x+1)^2-1\)
平方完成すると
\(y=a(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a}\)に変形できる。
頂点:\((-\frac{b}{2a}, -\frac{b^2-4ac}{4a})\)
軸:直線 \(x=-\frac{b}{2a}\)
例題
2次関数\(y=x^2-4x+2\)の頂点と軸を求めよ。
解答
\(y=x^2-4x+2\)
\(=(x-2)^2-2\)
より
頂点:\((2, -2)\)
軸:直線\(x=2\)
2.平行移動
\(x\)方向に\(p\), \(y\)軸方向に\(q\)平行移動
①点\((a, b)\) → \((a+p, b+p)\)
②関数\(y=f(x)\)
→ \(y-q=f(x-p)\) すなわち \(y=f(x-p)+q\)
※関数の平行移動は
\(x\) → \(x-p\)
\(y\) → \(y-q\)
に置き換えればOK
例題
①点\\((2, -3)\)を\(x\)軸方向に\(1\), \(y\)軸方向に\(-2\)だけ平行移動した点の座標を求めよ。
②放物線\(y=x^2-4x+2\)を, \(x\)軸方向に\(1\), \(y\)軸方向に\(-2\)だけ平行移動して得られる放物線の方程式を求めよ。
解答
①\((2+1, -3-2)\)より 点\((3, -5)\)
②\(x\) → \(x-1\)
\(y\) → \(y+2\)
に置き換えればよいから
\(y+2=(x-1)^2-4(x-1)+2\)より
\(y=(x^2-2x+1)-4x+4+2-2\)
\(y=x^2-6x+5\)
3.対称移動
①点\((a, b)\)
\(x\)軸対称 → \((a, -b)\)
\(y\)軸対称 → \((-a, b)\)
原点対称 → \((-a, -b)\)
②関数\(y=f(x)\)
\(x\)軸対称 → \(-y=f(x)\) ⇔\(y=-f(x)\)
\(y\)軸対称 → \(y=f(-x)\)
原点対称 → \(-y=f(-x)\) ⇔\(y=-f(-x)\)
※\(x\)軸対称は\(y\),
\(y\)軸対称は\(x\),
原点対称は\(x, y\)両方
の符号が変わると覚える
例題
①点\((2, -3)\)を\(x\)軸, \(y\)軸, 原点に関して,それぞれ対称移動して得られる各点の座標を求めよ。
②放物線\(y=x^2-4x+2\)を, \(x\)軸, \(y\)軸, 原点に関して,それぞれ対称移動して得られる放物線の方程式を求めよ。
解答
①
\(x\)軸対称:点\((2, 3)\)
\(y\)軸対称:点\((-2, -3)\)
原点対称:\((-2, 3)\)
②
\(x\)軸対称:\(-y= x^2-4x+2\) すなわち \(y=-x^2+4x-2\)
\(y\)軸対称:\(y= ((-x)^2-4(-x)+2\) すなわち \(y=x^2+4x+2\)
原点対称:\(-y= ((-x)^2-4(-x)+2\) すなわち \(y=-x^2-4x-2\)
4.2次関数の最大値・最小値
STEP① 平方完成して、\(y=a(x-p)^2+q\)の形にする。
STEP② 頂点・軸を求め、グラフをかく
STEP③ グラフの\(y\)座標が最も大きい値(最大値)、最も小さい値(最小値)を求める
例題
2次関数\(y=2x^2-12x+22(0 \leq x \leq 4) \)の最大値・最小値を求めよ。
解答
\(y=2x^2-12x+22\)
\(y=2(x-3)^2+4\) より←①平方完成
頂点\((3, 4)\)
軸:直線\(x=3\)
端点:\(x=0のときy=22, x=4のときy=6\)←②頂点・軸・端点
③グラフをかく
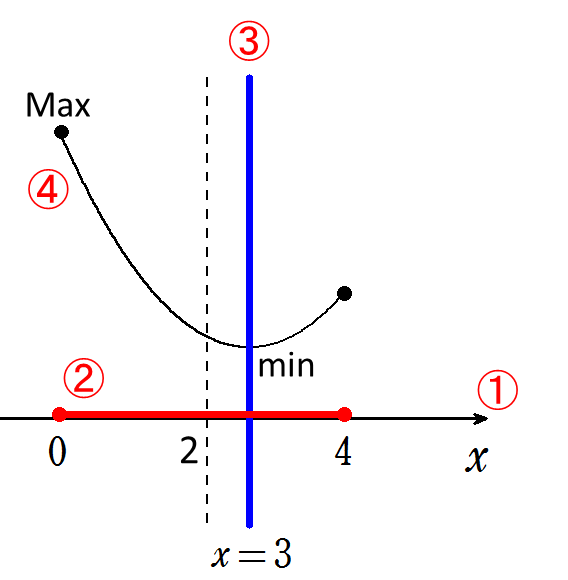
よって、グラフより
\(x=0のとき最大値22\)
\(x=3のとき最小値4\) ← ④最大値・最小値を求める。
5.2次関数の決定
STEP① 求める2次関数をおく
①放物線の頂点・軸・最大値・最小値関係がわかっている場合
→ \(y=a(x-p)^2+q\)とおく
②グラフが通る3点がわかっている場合
→ \(y=ax^2+bx+c\)とおく
③\(x\)軸との交点がわかっている場合
→ \(y=a(x-α)(x-β)\) とおく
STEP② STEP①でおいた2次関数に条件をあてはめて立式する
STEP③ 立式した方程式を解き、条件を満たす2次関数を求める。
例題
①頂点が点\((2, 3)\)で, 点\((1,5)\)を通る2次関数を求めよ。
②\(3点(-1,9),(1,-1),(2,0)\)を通る2次関数を求めよ。
③\(x\)軸との交点が\((-1,0), ( 2, 0)\)であり,\(y\)切片が\(-2\)である2次関数を求めよ。
解答
①頂点が点\((2, 3)\)より,求める2次関数を
\(y=a(x-2)^2+3\)
とおく
これが,点\((1, 5)\)を通るから,
\(5=a(1-2)^2+3\)
\(a=2\)
よって
\(y=2(x-2)^2+3\)
②求める2次関数を
\(y=ax^2+bx+c\)
とおく
これが,\(3点(-1,9),(1,-1),(2,0)\)を通るから,
\(9=a \cdot (-1)^2+b \cdot (-1)+c\)
\(-1=a \cdot 1^2+b \cdot 1+c\)
\(y=a \cdot 2^2+b \cdot 2+c\)
これを解くと、
\(a=2, b=-5, c=2\)
より
\(y=2x^2-5x+2\)
③\(x\)軸との交点が\((-1,0), ( 2, 0)\)より,求める2次関数を
\(y=a(x+1)(x-2)\)
とおく
\(y\)切片が\(-2\)より
\(-2=a(0+1)(0-2)\)
よって
\(a=1\)
であるから
\(y=(x+1)(x-2)\)
すなわち
\(y=x^2-x-2\)
6.2次方程式
2次方程式\(ax^2+bx+c=0\)の解は
\(x=\frac{-b±\sqrt{b^2-4ac}}{2a}\)
例題
2次方程式\(x^2+5x+3=0\)を解け。
解答
\(x=\frac{-5±\sqrt{5^2-4 \cdot 1 \cdot 3}}{2 \cdot 1}\)
\(=\frac{-5±\sqrt{13}}{2}\)
2次方程式\(ax^2+2b’x+c=0\)(\(x\)の項が偶数の場合)の解は
\(x=\frac{-b’±\sqrt{b’^2-ac}}{a}\)
例題
2次方程式\(x^2+4x+2=0\)を解け。
解答
\(x=\frac{-2±\sqrt{2^2-1 \cdot 2}}{1}\)
\(=-2±\sqrt{2}\)
①因数分解の利用
⇒ 左辺が因数分解できるとき
②平方根の利用
⇒ \(x^2=p\)の形になるとき(\(x\)の項がないとき)
③解の公式の利用
⇒ ①,②以外のとき
例題
次の2次方程式を解け。
①\(x^2-5x+6=0\)
②\(2x^2=6\)
③\(3x^2-5x-1=0\)
解答
①\(x^2-5x+6=0\)
\((x-2)(x-3)=0\)
より
\(x=2, 3\)
②\(2x^2=6\)
\(x^2=3\)
よって
\(x=\pm \sqrt{3}\)
③\(x=\frac{-(-5)±\sqrt{(-5)^2-4 \cdot 3 \cdot (-1)}}{2 \cdot 3}\)
\(=\frac{5±\sqrt{37}}{6}\)
2次方程式 \(ax^2+bx+c=0\)の判別式\(D=b^2-4ac\)において
\(D>0\) ⇔ 異なる2つの実数解をもつ(解は2個)
\(D=0\) ⇔ 重解をもつ(解は1個)
\(D<0\) ⇔ 実数解をもたない(解は0個)
※特に、\(D \geq 0\) ⇔ 実数解をもつ(解は1個or2個)
例題
2次方程式\(x^2+5x+m=0\)が異なる2つの実数解をもつとき,定数\(m\)の値の範囲を求めよ。
解答
異なる2つの実数解をもつとき,2次方程式\(x^2+5x+m=0\)の判別式\(D>0\)より
\(D=5^2-4 \cdot 1 \cdot m > 0\)
より
\(25-4m>0\)
\(m<\frac{25}{4}\)
2次方程式 \(ax^2+2b’x+c=0\)の判別式\(D/4={b’}^2-ac\)において
\(D/4>0\) ⇔ 異なる2つの実数解をもつ(解は2個)
\(D/4=0\) ⇔ 重解をもつ(解は1個)
\(D/4<0\) ⇔ 実数解をもたない(解は0個) ※特に、\(D/4 \geq 0\) ⇔ 実数解をもつ
例題
2次方程式\(x^2-4x+m=0\)が実数解をもたないとき,定数\(m\)の値の範囲を求めよ。
解答
実数解をもたないとき,2次方程式\(x^2-4x+m=0\)の判別式\(D<0\)より
\(D=(-2)^2-1 \cdot m < 0\)
より
\(4-m<0\)
\(m>4\)
7.2次関数のグラフと\(x\)軸の交点の個数
2次関数\(y=ax^2+bx+c\) のグラフと\(x\)軸の交点の数は\(D=b^2-4ac\)において
\(D>0\) ⇔ 異なる2点で交わる(交点は2個)
\(D=0\) ⇔ 1点で接する(交点は1個)
\(D<0\) ⇔ 共有点をもたない(交点は0個)
※特に、\(D \geq 0\) ⇔ 交点をもつ(交点は1個or 2個)
例題
2次関数\(y=x^2-3x+m\)のグラフが\(x\)軸と接するとき,定数\(m\)の値を求めよ。
解答
\(x\)軸と接するとき,2次方程式\(x^2-3x+m=0\)の判別式\(D=0\)より
\(D=(-3)^2-4 \cdot 1 \cdot m = 0\)
より
\(9-4m=0\)
\(m=\frac{9}{4}\)
8.2次不等式の解
STEP① 2次方程式\(ax^2+bx+c=0\)を解き、2次関数\(y=ax^2+bx+c\) と\(x\)軸との交点を求める。
STEP② \(x\)軸との交点を利用して2次関数\(y=ax^2+bx+c\)のグラフをかく
STEP③ グラフから条件を満たす\(x\)の範囲を求める
例題
\(x^2-2x-3\lt0\)を解け。
解答
\(y=x^2-2x-3\)と\(x\)軸との交点を求めると
\(x^2-2x-3=0\)より
\((x+1)(x-3)=0\)
\(x=-1, 3\)
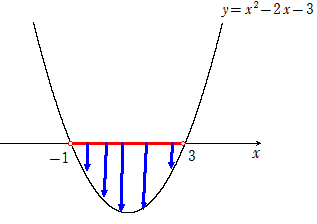
したがって、求める\(x\)の範囲は
\(-1<x<3\)









コメント