ここでは、【数学A】「図形の性質」でよく利用する公式(基礎知識)と例題を一覧にしています。
1.角の二等分線の公式
△ABCの\(\angle\)Aの内角の二等分線と辺BCとの交点Pは,辺BCをAB:ACに内分する
BP:PC=BA:AC

例題
右の図でAPは\(\angle\)Aの内角の二等分線とする。AB=8, AC=6 であるとき,
BP:PCを求めよ。

解答
APは\(\angle\)Aの内角の二等分線より
BP:PC=BA:AC=8:6=4:3
AB \(\ne\)AC である△ABCの\(\angle\)Aの外角の二等分線と辺BCの延長との交点Qは,辺BCをAB:ACに外分し、次が成り立つ
BQ:QC=BA:AC

例題
図のような, AB = 12, BC = 10, CA = 8 である三角形ABCにおいて, ∠A の外角の二等分線と辺BCの延長との交点をDとする。
辺 CD の長さを求めよ。

解答
ADは∠Aの外角の二等分線より
BD:CD=BA:AC=12:8=3:2
よって
(10 + CD) :CD =3:2
2(10 + CD) =3CD
CD = 20
2.三角形の外心・内心・重心
点Oが三角形ABCの外心
①点Oは3辺の垂直二等分線の交点
②点Oは外接円の中心(OA=OB=OC)


例題
次の図で点O は三角形ABC の外心であるとするとき,∠\(\alpha\) の値を求めよ。

解答
点O が三角形ABC の外心であるとき, 円周角の定理より
∠\(\alpha = 65 \times 2 = 130^{\circ}\)
点Iが三角形ABCの内心
①点Iは内角の二等分線の交点
②点Iは内接円の中心(ID=IE=IF)

例題
次の図で点I は三角形ABC の内心であるとするとき,∠\(\alpha\) の値を求めよ。

解答
点I が三角形ABC の内心であるとき, 線分AO, BO, CO は∠A, ∠B, ∠C の二等分線であるから,
\(\angle OAB = \angle OAC = 35^{\circ}\)
\(\angle OBA = \angle OBC = \beta^{\circ}\)
\(\angle OCB = \angle OCA = \gamma^{\circ}\)
より
\(2\beta + 2\gamma = 180^{\circ} – 70^{\circ} = 110^{\circ}\)
\(\beta + \gamma = 55^{\circ}\)
したがって、
\(\alpha = 180^{\circ} – 55^{\circ} = 125^{\circ}\)

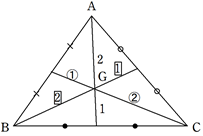
点Gが三角形ABCの重心
①点Gは3つの中線の交点。
②各頂点から中点までの比が2:1
例題
三角形ABCの重心をGとし,2点A, Gから直線BCに下した垂線を,それぞれAH, GK とするとき,
AH:GKを求めよ。

解答
辺BC の中点をMとする
AHとGKは平行であるから,
AH:GK = AM:GM
Gは三角形ABC の重心であるから
AG:GM = 2:1
よって AM:GM = 3:1
したがって
AH:GK = 3:1
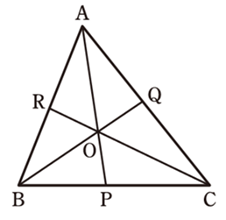
3.チェバの定理
図のような△ABC において
\(\displaystyle\frac{RB}{AR} \cdot \displaystyle\frac{PC}{BP} \cdot \displaystyle\frac{QA}{CQ} = 1\)
例題
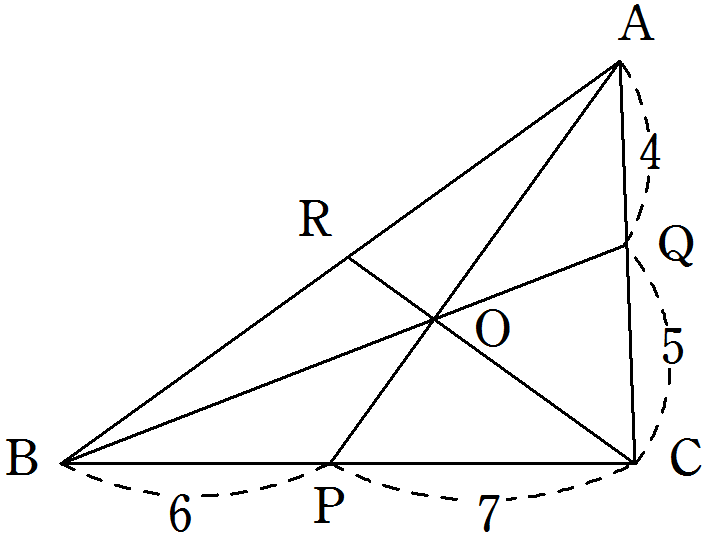
次の図の△ABC において, \(3\) 点\(P, Q, R\) は
それぞれ辺\(BC, CA, AB\)上の点です。
\(3\) つの線分\(AP, PQ, CR\) が1点\(O\) で交わるとき,
\(AR:RB\) を最も簡単な整数の比で表しなさい。
解答
△ABC においてチェバの定理より
\(\displaystyle\frac{RB}{AR} \times \displaystyle\frac{PC}{BP} \times \displaystyle\frac{QA}{CQ} =1 \)
\(\displaystyle\frac{RB}{AR} \times \displaystyle\frac{7}{6} \times \displaystyle\frac{4}{5} =1 \)
\(\displaystyle\frac{RB}{AR} = \displaystyle\frac{15}{14} \)
したがって、
\(\color{red}{AR : RB = 14 : 15}\)
4.メネラウスの定理
図のような△ABC と直線\(\ell\)において
\(\displaystyle\frac{RB}{AR} \cdot \displaystyle\frac{PC}{BP} \cdot \displaystyle\frac{QA}{CQ} = 1\)

例題
次の図の△ABC において, \(3\) 点\(P, Q, R\) は
それぞれ辺\(BC, CA, AB\)上の点です。
\(3\) つの線分\(AP, PQ, CR\) が1点\(O\) で交わるとき,
\(AO:OP\) を最も簡単な整数の比で表しなさい。

解答
三角形ABCと線分CRにおいて、メネラウスの定理より
\(\displaystyle\frac{QC}{AQ} \cdot \displaystyle\frac{BP}{CB} \cdot \displaystyle\frac{OA}{PO} = 1\) より
\(\displaystyle\frac{5}{4} \cdot \displaystyle\frac{6}{13} \cdot \displaystyle\frac{OA}{PO} = 1\) より
\(\displaystyle\frac{OA}{PO} = \displaystyle\frac{26}{15}\)
よって
AO:OP=26:15
5.円周角の定理とその逆
①図において、4点A, B, P, Q が同一円周上にあるとき、
\(\angle\)APB =\(\angle\)AQB

②円周角は中心角の半分
※特に、直径(中心角\(180^\circ\))がつくる円周角は直角(\(90^\circ\))

例題
図において、4点A, B, P, Q が同一円周上にあり、∠AQB = 50° のとき, ∠APBの値を求めよ。

解答
4点A, B, P, Q が同一円周上にあるから、円周角の定理より
\(\angle\)APB =\(\angle\)AQB = 50°
図において、\(\angle\)APB =\(\angle\)AQB が成り立つとき、
4点A, B, P, Q は同一円周上にある
(四角形ABPQは円に内接する)

6.円に内接する四角形
四角形が円に内接するとき、
①対角の和は \(180^\circ\)
②内角は,その対角の外角に等しい

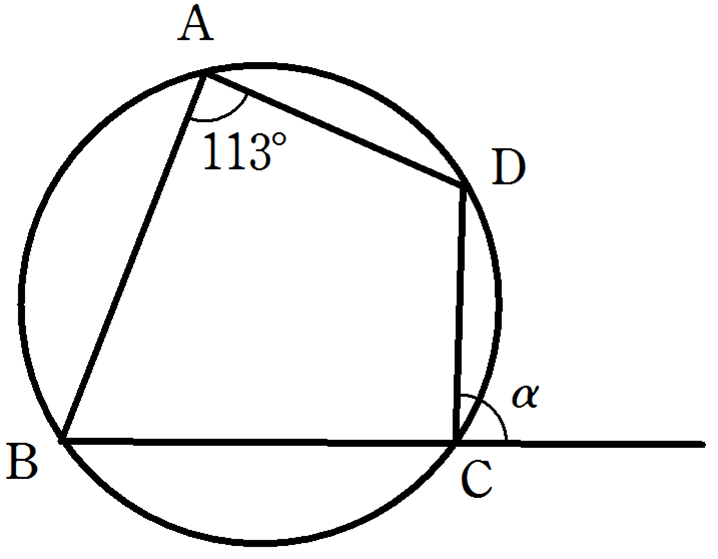
例題
右の図のように,四角形ABCDが円に内接し,
\(\angle\mathrm{BAD} = 113^{\circ}\)です。
このとき,
\(\angle\mathrm{\alpha}\)
の大きさを求めなさい。
解答
四角形ABCDは円に内接しているので
\(\alpha = \angle\mathrm{BAD} = 113^{\circ}\)
よって
\(\color{red}{\alpha = 113^{\circ}}\)
7.接線と弦の作る角
図において、直線ATが円Oの接線であるとき、
\(\angle ACB = \angle BAT\)

例題
右の図で,直線\(\ell\) は円の接線,Aはその接点である。
このとき,角\(\theta\)を求めよ。

解答
\(\theta = 55^{\circ}\)
8.方べきの定理
①\(PA \cdot PB =PC \cdot PD\)
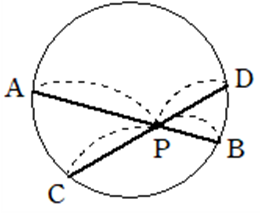
②\(PA \cdot PB =PC \cdot PD\)
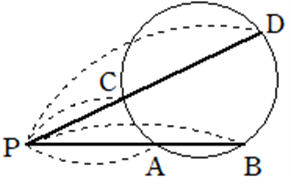
③\(PA \cdot PB =PT^2\)
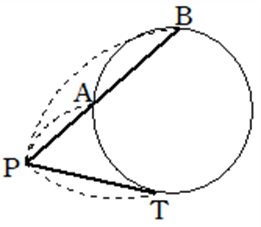
例題
次の図において、CPの長さを求めよ。

解答
方べきの定理より
\(PA \cdot PB =PC \cdot PD\) より
\(4 \times 2 = PC \times 3\)
\(CP = \displaystyle\frac{8}{3}\)
9.多面体
多角形の面で囲まれた立体を多面体といい、へこみのない多面体を凸多面体という
凸多面体の頂点の数を\(v\), 辺の数を\(e\), 面の数を\(f\)とすると、
\(v-e+f=2\)
が常に成り立つ



コメント