1.角の二等分線の公式
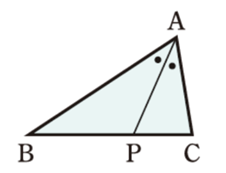
△ABCの\(\angle\)Aの内角の二等分線と辺BCとの交点Pは,辺BCをAB:ACに内分し、次が成り立つ
BP:PC=BA:AC
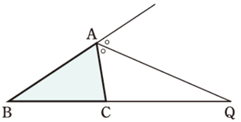
AB \(\ne\)AC である△ABCの\(\angle\)Aの外角の二等分線と辺BCの延長との交点Qは,辺BCをAB:ACに外分し、次が成り立つ
BQ:QC=BA:AC
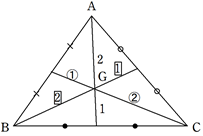
2.三角形の外心・内心・重心
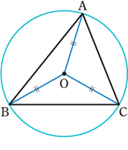
点Oが三角形ABCの外心
①点Oは3辺の垂直二等分線の交点
②点Oは外接円の中心(OA=OB=OC)
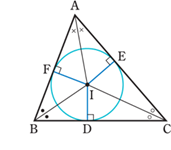
点Iが三角形ABCの内心
①点Iは内角の二等分線の交点
②点Iは内接円の中心(ID=IE=IF)
点Gが三角形ABCの重心
①点Gは3つの中線の交点。
②各頂点から中点までの比が2:1
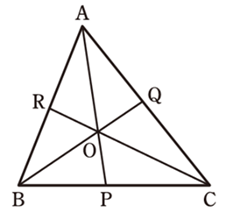
3.チェバの定理
図において、
\(\frac{RB}{AR} \cdot \frac{PC}{BP} \cdot \frac{QA}{CQ}=1\)
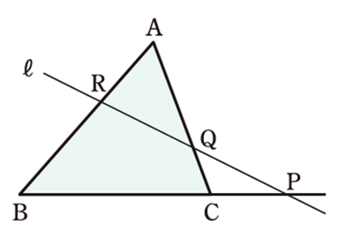
4.メネラウスの定理
図において、
\(\frac{RB}{AR} \cdot \frac{PC}{BP} \cdot \frac{QA}{CQ}=1\)
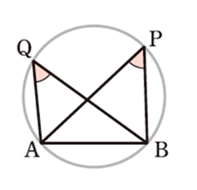
5.円周角の定理とその逆
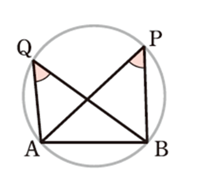
① 図において、4点A, B, P, Q が同一円周上にあるとき、
\(\angle\)APB =\(\angle\)AQB
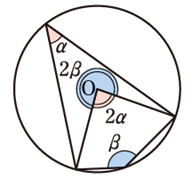
② 円周角は中心角の半分
※特に、直径(中心角\(180^{\circ}\))がつくる円周角は直角(\(90^{\circ}\))
図において、\(\angle\)APB =\(\angle\)AQB が成り立つとき、
4点A, B, P, Q は同一円周上にある
(四角形ABPQは円に内接する)
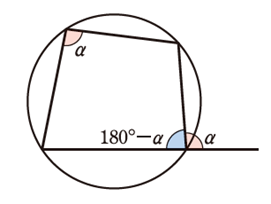
6.円に内接する四角形
四角形が円に内接するとき、
①対角の和は \(180^{\circ}\)
②内角は,その対角の外角に等しい
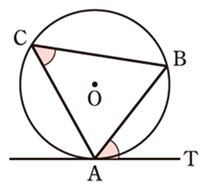
7.接線と弦の作る角
図において、直線ATが円Oの接線であるとき、
\(\angle ACB = \angle BAT\)
8.方べきの定理
図において
\(PA \cdot PB =PC \cdot PD\)
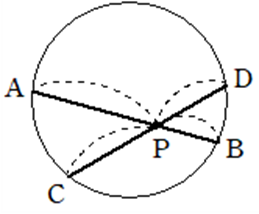
図において
\(PA \cdot PB =PC \cdot PD\)
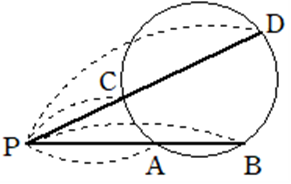
図において
\(PA \cdot PB =PT^2\)
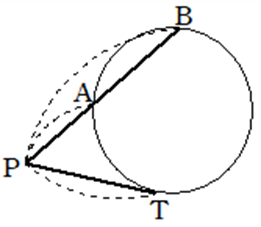
9.多面体
多角形の面で囲まれた立体を多面体といい、へこみのない多面体を凸多面体という
凸多面体の頂点の数を\(v\), 辺の数を\(e\), 面の数を\(f\)とすると、
\(v-e+f=2\)
が常に成り立つ








コメント