ここでは、【数学II】「三角関数」でよく利用する公式(基礎知識)や例題を一覧にしてまとめています。
1.弧度法
半径1の円の弧の長さに対する角度 → 弧度法
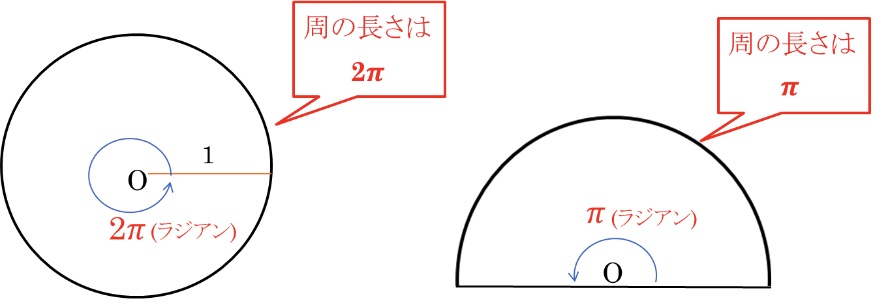
\(180^\circ = \pi\)ラジアン
例題
(1)\(30^{\circ}\) を弧度法で表せ。
(2)\(\displaystyle\frac{2}{3}\pi\) を度数法で表せ。
解答
(1) \(30^{\circ} = \displaystyle\frac{30}{180}\pi = \displaystyle\frac{\pi}{6}\)
(2) \(\displaystyle\frac{2}{3}\pi = \displaystyle\frac{2}{3} \times 180^{\circ} = 120^{\circ}\)
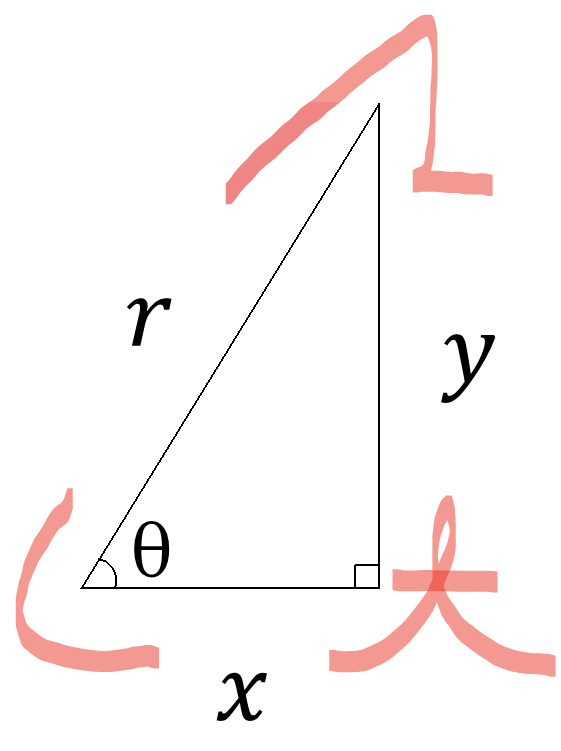
2.三角関数の定義
①\(\sin\theta = \displaystyle\frac{y}{r}\)
②\(\cos\theta = \displaystyle\frac{x}{r}\)
③\(\tan\theta = \displaystyle\frac{y}{x}\)
\(\theta\)の関数とみたとき、これらを三角関数という
例題
次の直角三角形ABCにおける \(\sin\theta, \cos\theta, \tan\theta\) の値を求めよ。

解答
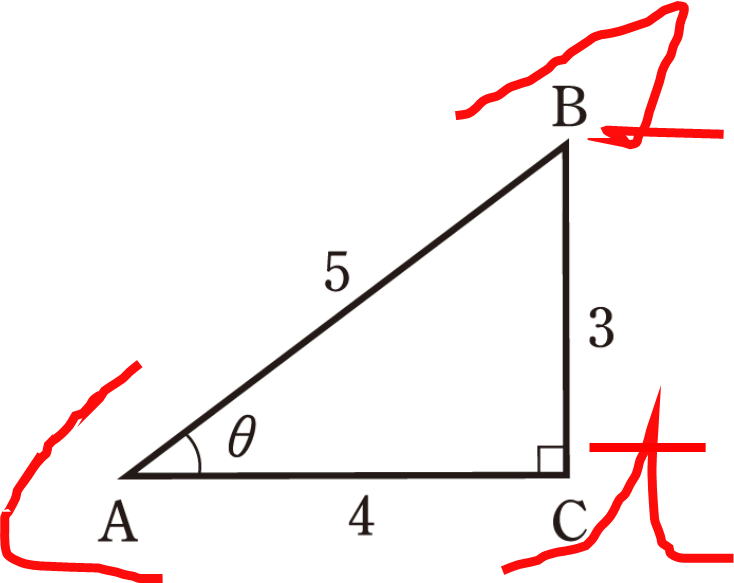
\(\sin\theta=\frac{3}{5}\)
\(\cos\theta=\frac{4}{5}\)
\(\tan\theta=\frac{3}{4}\)
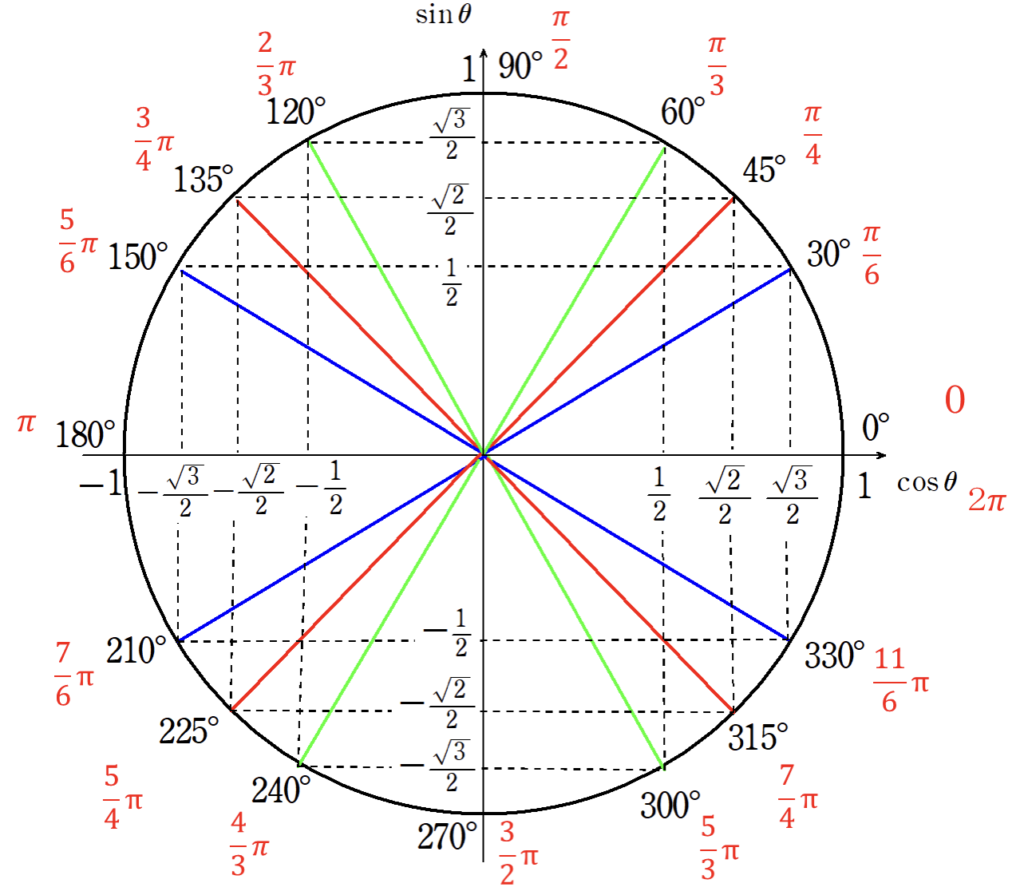
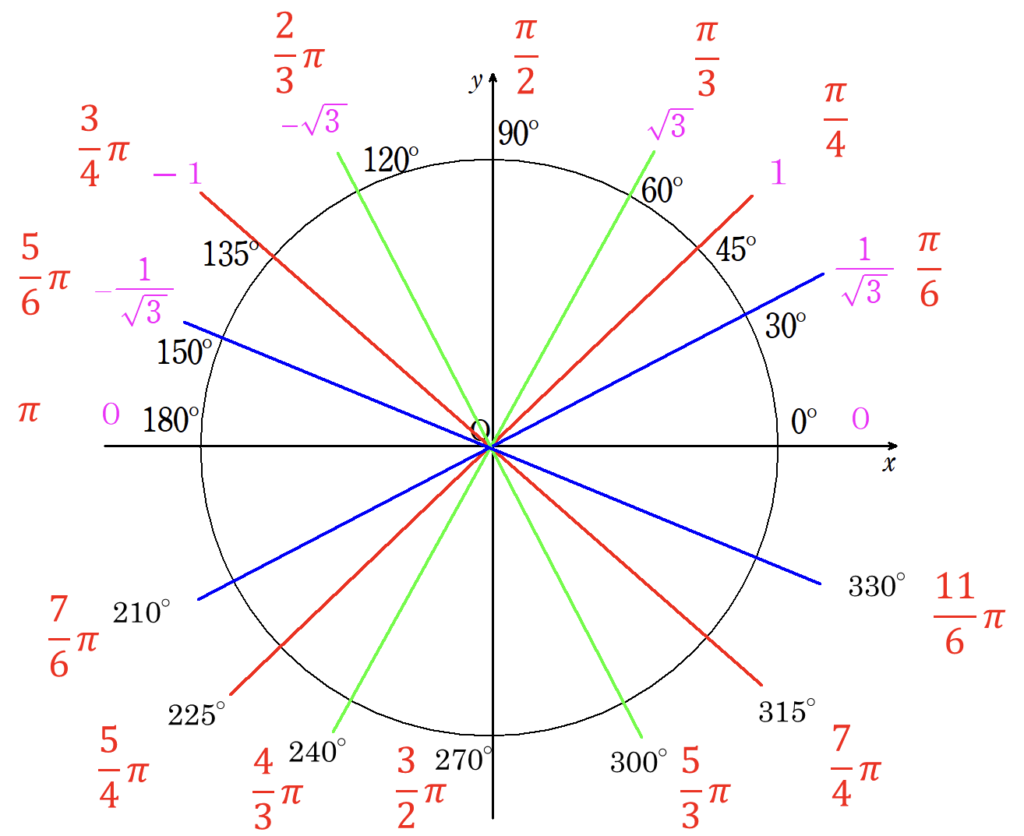
3.三角関数の値
\(\cos\)の値 → 単位円上の\(x\)座標
\(\sin\)の値 → 単位円上の\(y\)座標
例題
次の値を求めよ。
(1)\(\cos \displaystyle\frac{5}{6}\pi\)
(2)\(\sin \displaystyle\frac{5}{4}\pi\)
解答
(1)\(\cos \displaystyle\frac{5}{6}\pi = -\displaystyle\frac{\sqrt{3}}{2}\)
(2)\(\sin \displaystyle\frac{5}{4}\pi = -\displaystyle\frac{\sqrt{2}}{2}\)
\(\tan\)の値 → 直線の傾き
例題
\(\tan \displaystyle\frac{7}{4}\pi\) の値を求めよ。
解答
\(\tan \displaystyle\frac{7}{4}\pi = -1\)
- \(-1 \leq \cos\theta \leq 1\)
- \(-1 \leq \sin\theta \leq 1\)
- \(\tan \theta\) → 実数全体
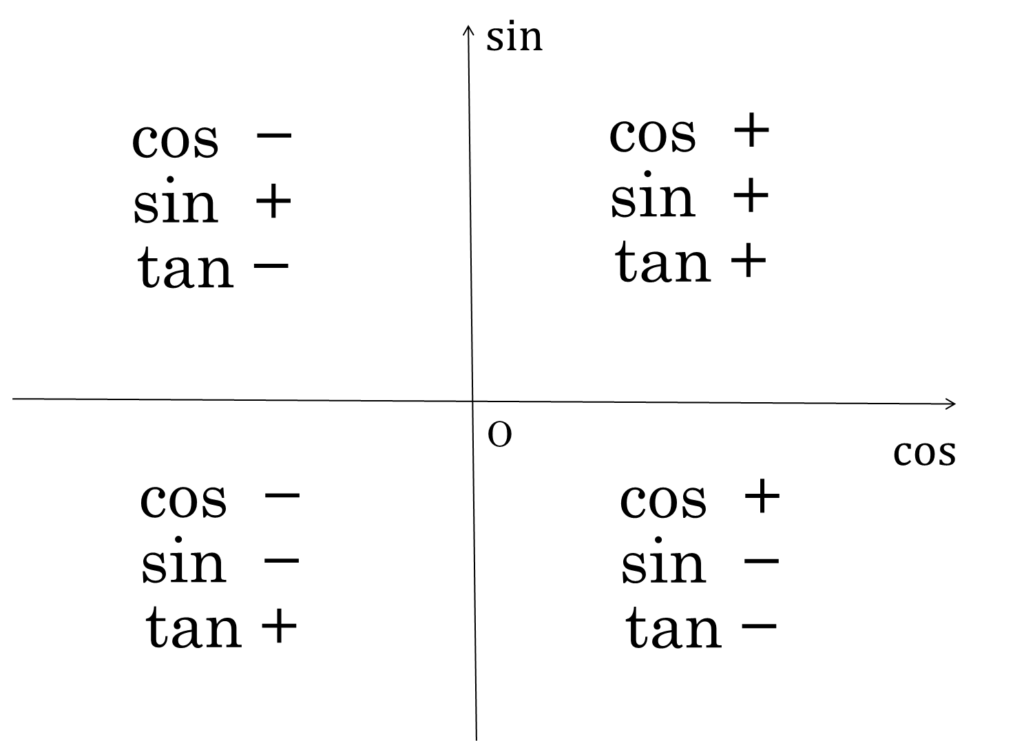
4.三角関数の相互関係
- \(\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}\)
- \(\sin^2{\theta}+\cos^2{\theta}=1\)
- \(1+\tan^2{\theta}=\displaystyle\frac{1}{\cos^2{\theta}}\)
例題
\(\theta\) の動径が第3象限にあり,\(\sin\theta = -\displaystyle\frac{4}{5}\) のとき,\(\cos\theta, \tan\theta\) の値を求めよ。
解答
\(\theta\) の動径が第3象限より,\(\cos\theta < 0\)
よって,\(\sin^2{\theta}+\cos^2{\theta}=1\) から
\(\cos\theta = – \sqrt{1 – \sin^{2}\theta} = – \sqrt{1 – \left(-\displaystyle\frac{4}{5}\right)^2} = -\displaystyle\frac{3}{5}\)
また,
\(\tan\theta = \displaystyle\frac{\sin\theta}{\cos\theta} = \left(-\displaystyle\frac{4}{5}\right) \div \left(-\displaystyle\frac{3}{5}\right) = \displaystyle\frac{4}{3}\)
5.三角関数の性質
- \(\sin(\theta + 2n\pi) = \sin\theta\)
- \(\cos(\theta + 2n\pi) = \cos\theta\)
- \(\tan(\theta + n\pi) = \tan\theta\)
例題
次の値を求めよ。
(1)\(\sin\displaystyle\frac{7}{3}\pi \)
(2)\(\cos\displaystyle\frac{7}{3}\pi\)
(3)\(\tan\displaystyle\frac{5}{4}\pi \)
解答
(1)\(\sin\displaystyle\frac{7}{3}\pi = \sin\left(\displaystyle\frac{\pi}{3} + 2\pi\right) = \sin\displaystyle\frac{\pi}{3} = \displaystyle\frac{\sqrt{3}}{2}\)
(2)\(\cos\displaystyle\frac{7}{3}\pi = \cos\left(\displaystyle\frac{\pi}{3} + 2\pi\right) = \cos\displaystyle\frac{\pi}{3} = \displaystyle\frac{1}{2}\)
(3)\(\tan\displaystyle\frac{5}{4}\pi = \tan\left(\displaystyle\frac{\pi}{4} + \pi\right) = \tan\displaystyle\frac{\pi}{4} = 1\)
- \(\sin(-\theta) = -\sin\theta\)
- \(\cos(-\theta) = \cos\theta\)
- \(\tan(-\theta) = -\tan\theta\)
例題
次の値を求めよ。
(1)\(\sin\left(-\displaystyle\frac{\pi}{3}\right)\)
(2)\(\cos\left(-\displaystyle\frac{\pi}{3}\right)\)
(3)\(\tan\left(-\displaystyle\frac{\pi}{3}\right)\)
解答
(1)\(\sin\left(-\displaystyle\frac{\pi}{3}\right) = -\sin\displaystyle\frac{\pi}{3} = -\displaystyle\frac{\sqrt{3}}{2}\)
(2)\(\cos\left(-\displaystyle\frac{\pi}{3}\right) = \cos\displaystyle\frac{\pi}{3} = \displaystyle\frac{1}{2}\)
(3)\(\tan\left(-\displaystyle\frac{\pi}{3}\right) = -\tan\displaystyle\frac{\pi}{3} = -\sqrt{3}\)
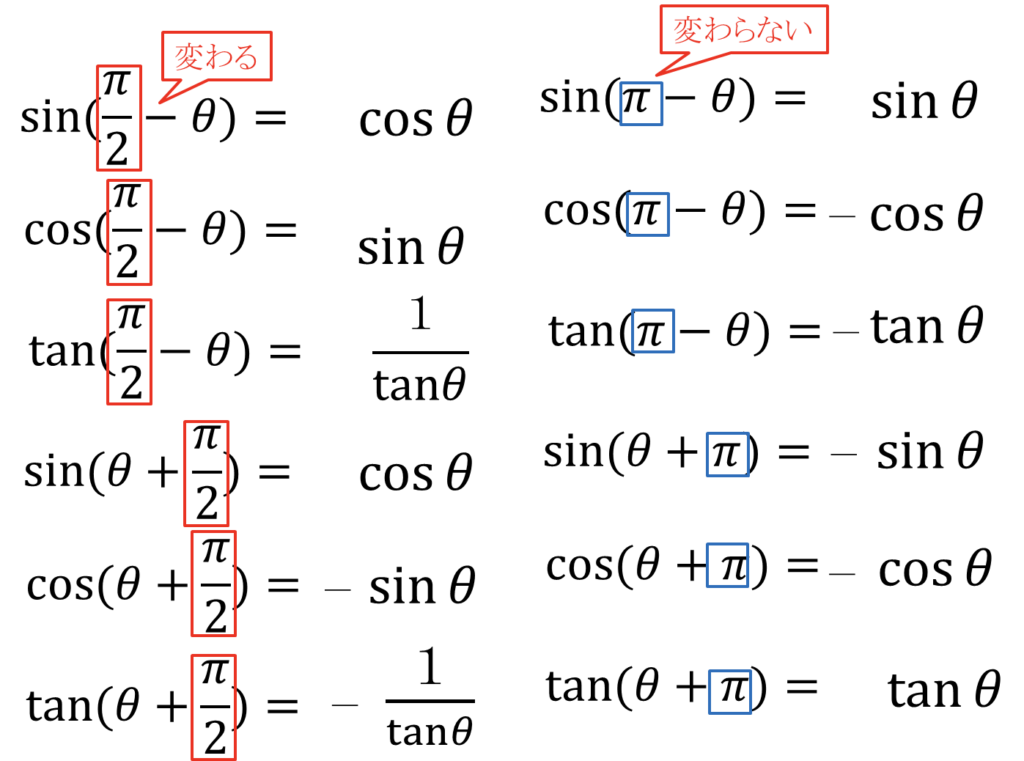
※\(\displaystyle\frac{\pi}{2}\)関連の加減 → 変わる
\(\sin ⇒ \cos\)
\(\cos ⇒ \sin\)
\(\tan ⇒ \displaystyle\frac{1}{\tan}\)
※\(\pi\)関連の加減 → 変わらない
\(\sin ⇒ \sin\)
\(\cos ⇒ \cos\)
\(\tan ⇒ \tan \)
と覚える
例題
\(\sin\left(\theta + \pi\right) + \cos\left(\displaystyle\frac{\pi}{2} – \theta\right)\) を計算し,簡単にせよ。
解答
\(\sin(\theta + \pi) + \cos\left(\displaystyle\frac{\pi}{2} – \theta\right)\)
\(= -\sin\theta + \sin\theta\)
\(= 0\)
6.三角関数のグラフ
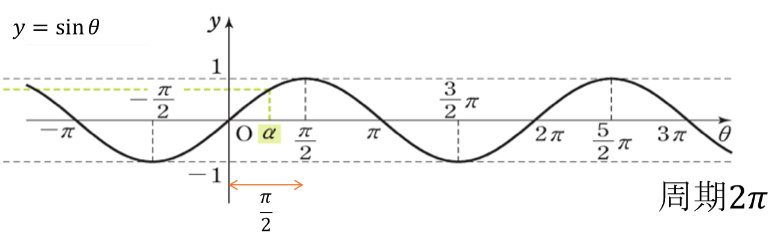
周期:\(2\pi\), 原点対称
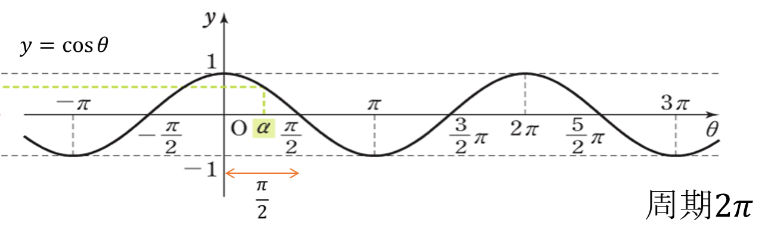
周期:\(2\pi\), \(y\)軸対称
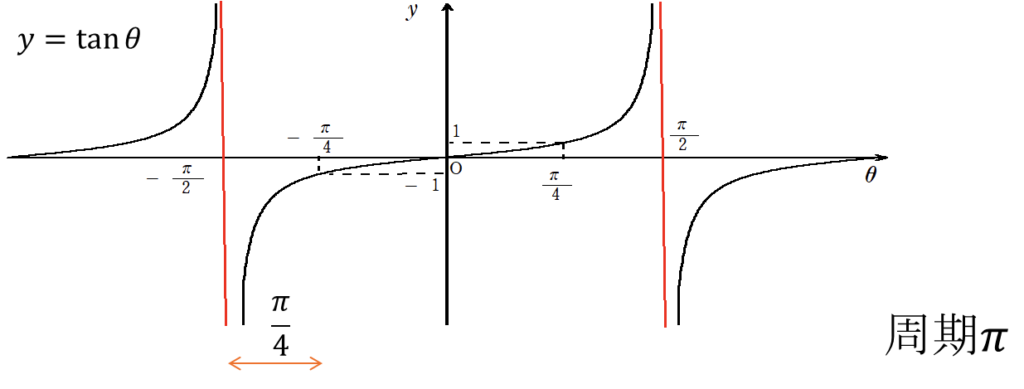
周期:\(\pi\), 原点対称
7.加法定理
- \(\sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta\)
- \(\sin(\alpha – \beta) = \sin\alpha\cos\beta – \cos\alpha\sin\beta\)
- \(\cos(\alpha + \beta) = \cos\alpha\cos\beta – \sin\alpha\sin\beta\)
- \(\cos(\alpha – \beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta\)
- \(\tan(\alpha+\beta) = \displaystyle\frac{\tan\alpha + \tan\beta}{1 – \tan\alpha \tan\beta}\)
- \(\tan(\alpha – \beta) = \displaystyle\frac{\tan\alpha – \tan\beta}{1 + \tan\alpha \tan\beta}\)
例題
\(\sin75^{\circ}\) の値を求めよ。
解答
\(\sin75^{\circ}\)
\(= \sin(30^{\circ} + 45^{\circ})\)
\(= \sin30^{\circ} \cdot \cos45^{\circ} + \cos30^{\circ} \cdot \sin45^{\circ}\)
\(= \displaystyle\frac{1}{2} \cdot \displaystyle\frac{\sqrt{2}}{2} + \displaystyle\frac{\sqrt{3}}{2} \cdot\displaystyle\frac{\sqrt{2}}{2}\)
\(= \displaystyle\frac{\sqrt{2}}{4} + \displaystyle\frac{\sqrt{6}}{4}\)
8.2倍角・半角の公式
①\(\sin2\theta = 2\sin\theta\cos\theta\)
②\(\cos2\theta = \cos^2\theta – \sin^2\theta\)
\(= 1 – 2\sin^2\theta\)
\(=2\cos^2\theta – 1\)
③\(\tan2\theta = \displaystyle\frac{2\tan\theta}{1 – \tan^2\theta}\)
例題
\(\cos\theta = \displaystyle\frac{3}{5}\) であるとき,\(\cos2\theta\) の値を求めよ。
解答
\(\cos2\theta = 2\cos^2\theta – 1\)
\(= 2 \cdot \left(\displaystyle\frac{3}{5}\right)^2 – 1\)
\(= 2 \cdot \left(\displaystyle\frac{9}{25}\right) – 1\)
\(= \displaystyle\frac{18}{25} – 1\)
\(= -\displaystyle\frac{7}{25}\)
①\(\sin^2\theta = \displaystyle\frac{1 – \cos2\theta}{2}\)
②\(\cos^2\theta = \displaystyle\frac{1 + \cos2\theta}{2}\)
③\(\tan^2\theta = \displaystyle\frac{1 – \cos2\theta}{1 + \cos2\theta }\)
①\(\sin^2\displaystyle\frac{\theta}{2} = \displaystyle\frac{1 – \cos\theta}{2}\)
②\(\cos^2\displaystyle\frac{\theta}{2} = \displaystyle\frac{1 + \cos\theta}{2}\)
③\(\tan^2\displaystyle\frac{\theta}{2} = \displaystyle\frac{1 – \cos\theta}{1 + \cos\theta }\)
例題
\(\sin\displaystyle\frac{\pi}{8}\) の値を求めよ。
解答
\(\sin^2\displaystyle\frac{\pi}{8}\)
\(= \displaystyle\frac{1 – \cos\frac{\pi}{4}}{2}\)
\(= \displaystyle\frac{1 – \frac{\sqrt{2}}{2}}{2}\)
\(= \displaystyle\frac{2 – \sqrt{2}}{4}\)
\(\sin\displaystyle\frac{\pi}{8} > 0\) より
\( \sin\displaystyle\frac{\pi}{8} = \sqrt{\displaystyle\frac{2 – \sqrt{2}}{4}}\)
\(= \displaystyle\frac{\sqrt{2 – \sqrt{2}}}{2}\)
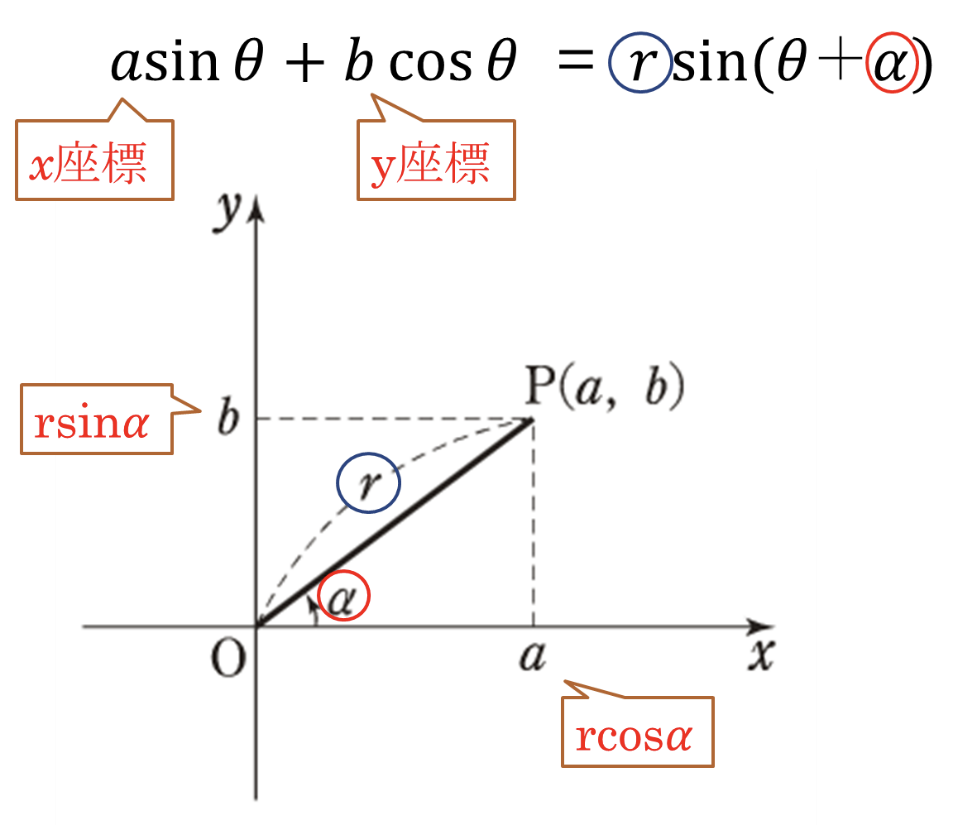
9.三角関数の合成
\(a\sin\theta + b\cos\theta = \sqrt{a^2 + b^2}\sin(\theta + \alpha)\)
※ただし、
\(\sin\alpha = \displaystyle\frac{b}{\sqrt{a^2 + b^2}}\)
\(\cos\alpha = \displaystyle\frac{a}{\sqrt{a^2 + b^2}}\)
例題
\(\sqrt{3}\sin\theta + \cos\theta\) を\(r\sin(\theta + \alpha)\) \(\left(-\displaystyle\frac{\pi}{2} \leq \alpha < \displaystyle\frac{\pi}{2}\right)\) の形にせよ。
解答
\(\sqrt{3}\sin\theta + \cos\theta = 2\sin\left(\theta + \displaystyle\frac{\pi}{6}\right)\)





コメント