【数と式】基本問題一覧〜一問一答式（高校数学I）〜

\(2^3 \times 2^5 = 2^{3+5} = 2^8 = 256\)

したがって

\(\color{red}{256}\)

（同じ底の累乗の積は、指数を足す：\(a^m \times a^n = a^{m+n}\)）

\(3^7 \div 3^4 = 3^{7-4} = 3^3 = 27\)

したがって

\(\color{red}{27}\)

（同じ底の累乗の商は、指数を引く：\(a^m \div a^n = a^{m-n}\)）

\((5^2)^3 = 5^{2 \times 3} = 5^6 = 15625\)

したがって

\(\color{red}{15625}\)

（累乗の累乗は、指数を掛ける：\((a^m)^n = a^{mn}\)）

\((2a^3)^4 = 2^4 \times (a^3)^4 = 16 \times a^{12} = 16a^{12}\)

したがって

\(\color{red}{16a^{12}}\)

（積の累乗は、各因数を累乗する：\((ab)^n = a^n b^n\)）

\(\displaystyle\frac{6^8}{6^5} = 6^{8-5} = 6^3 = 216\)

したがって

\(\color{red}{216}\)

（同じ底の累乗の商は、指数を引く）

\(\displaystyle\frac{(2x^2)^3 \times (3x)^2}{6x^5} = \displaystyle\frac{8x^6 \times 9x^2}{6x^5} = \displaystyle\frac{72x^8}{6x^5} = 12x^3\)

したがって

\(\color{red}{12x^3}\)

（各項を展開してから、同類項をまとめる）

\((x+3)(x-5)=x^2+(3-5)x+(3)\cdot(-5)=x^2-2x-15\)

したがって

\(\color{red}{x^2-2x-15}\)

\((2a+b)^2=(2a)^2+2(2a)(b)+b^2=4a^2+4ab+b^2\)

したがって

\(\color{red}{4a^2+4ab+b^2}\)

（\((A+B)^2=A^2+2AB+B^2\)の公式を使用する）

\((x+4)(x-4)=x^2-4^2=x^2-16\)

したがって

\(\color{red}{x^2-16}\)

(\((A+B)(A-B)=A^2-B^2\)の公式を使用)

\((x + y)^2 – 3x(2x – y)\)

\(= x^2 + 2xy + y^2 – 6x^2 + 3xy\)

\(= -5x^2 +5xy + y^2\)

よって

\( \color{red}{-5x^2 +5xy + y^2}\)

\((a + 3)(2a -1) – 3a(a – 1)\)

\(= 2a^2 – a + 6a -3 – 3a^2 + 3a\)

\(= -a^2 +8a -3 \)

よって

\(\color{red}{-a^2 +8a -3} \)

\((x + 3)(x – 5) – (3 – 2x)^2\)

\(= x^2 -2x -15 – (9 – 12x + 4x^2)\)

\(= x^2 -2x -15 – 9 +12x -4x^2\)

\(= -3x^2 +10x -24\)

よって

\( \color{red}{-3x^2 +10x -24}\)

\((3a + b)(-4a +5b) – (a + b)(a -b)\)

\(= -12a^2 + 15ab -4ab +5b^2 – (a^2 – b^2)\)

\(= -12a^2 +11ab + 5b^2 – a^2 + b^2\)

\(= -13a^2 +11ab + 6b^2\)

よって

\(\color{red}{-13a^2 +11ab + 6b^2}\)

\((2x + y)(2x – y ) – 4x(5 – x)\)

\(= 4x^2 – y^2 – 20x +4x^2\)

\(= 8x^2 – 20x – y^2\)

よって

\(\color{red}{8x^2 – 20x – y^2}\)

\((x+y)(x-y)=x^2-y^2\) より

\((x+y)(x-y)(x^2+y^2) = (x^2-y^2)(x^2+y^2)=x^4-y^4\)

したがって

\(\color{red}{x^4-y^4}\)

\((x+2)(x+3)=x^2+5x+6\)より

\((x+2)(x+3)(x+4)\)

\(= (x^2+5x+6)(x+4)\)

\(= x^3+4x^2+5x^2+20x+6x+24\)

\(=x^3+9x^2+26x+24\)

したがって

\(\color{red}{x^3+9x^2+26x+24}\)

\((x^2 – 3x +1)^2\)

\(= (x^2)^2 + (-3x)^2 + 1^2 + 2\cdot (x^2) \cdot (-3x) + 2\cdot (-3x) \cdot 1 + 2\cdot 1 \cdot (x^2)\)

\(= x^4 + 9x^2 + 1 – 6x^3 – 6x + 2x^2\)

\(= x^4 – 6x^3 + 11x^2 – 6x +1\)

よって

\( \color{red}{x^4 – 6x^3 + 11x^2 – 6x +1}\)

\((a^2 + 2a – 3)^2\)

\(= (a^2)^2 + (2x)^2 + (-3)^2 + 2\cdot (a^2) \cdot (2a) + 2\cdot (2a) \cdot (-3) + 2\cdot (-3) \cdot (a^2)\)

\(= a^4 + 4a^2 + 9 + 4a^3 – 12a – 6a^2\)

\(= a^4 + 4a^3 – 2a^2 – 12a + 9\)

よって

\( \color{red}{a^4 + 4a^3 – 2a^2 – 12a + 9}\)

\((x^2 + 2x + 7)(x^2 – 2x + 7)\)

\(= \{(x^2 + 7) + 2x\}\{(x^2 + 7) – 2x\}\)

\(= (x^2 + 7)^2 – (2x)^2\)

\(= (x^4 + 14x^2 +49) – 4x^2\)

\(= x^4 + 10x^2 +49\)

よって

\( \color{red}{x^4 + 10x^2 +49}\)

\(3×4=12、3+4=7\)なので

\(x^2+7x+12 = (x+3)(x+4)\)

したがって

\(\color{red}{(x+3)(x+4)}\)

\(x^2-6x+9 = x^2-2(x)(3)+3^2=(x-3)^2\)

したがって

\(\color{red}{(x-3)^2}\)

(\(A^2-2AB+B^2=(A-B)^2\))の公式を使用

\(4x^2-9 = (2x)^2-3^2 = (2x+3)(2x-3)\)

したがって

\(\color{red}{(2x+3)(2x-3)}\)

(\(A^2-B^2=(A+B)(A-B)\)の公式を使用)

\(4x^2 + 12xy + 9y^2\)

\(= (2x)^2 + 2\cdot (2x)\cdot (3y) + (3y)^2\)

\(= (2x +3y)^2\)

よって

\(\color{red}{(2x +3y)^2} \)

\(a^2 -5ab +6b^2\)

\(= a^2 + (-3b-2b)\cdot a +(-3b)\cdot(-2b)\)

\(= (a – 3b)(a – 2b)\)

よって

\(\color{red}{ (a – 3b)(a – 2b)}\)

\(25x^2 – 16y^2\)

\(= (5x)^2 – (4y)^2\)

\(= (5x + 4y)(5x – 4y)\)

よって

\( \color{red}{(5x + 4y)(5x – 4y)}\)

\(x^2 + xy – 20y^2\)

\(= x^2 + (5y -4y)\cdot x + (5y)\cdot (-4y)\)

\(= (x+5y)(x-4y)\)

よって

\(\color{red}{(x+5y)(x-4y)}\)

たすき掛けは次のようになる

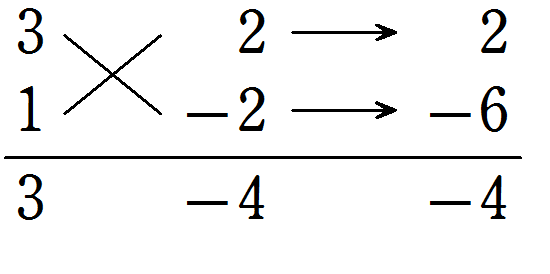
したがって

\( \color{red}{(3x + 2y)(x – 2y)}\)

たすき掛けは次のようになる

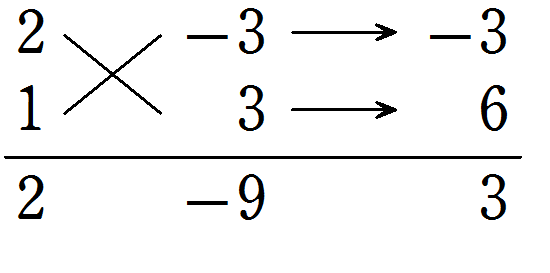
したがって

\(\color{red}{(2a – 3b)(a + 3b)} \)

\(2a^2 b + a^2 – 8b – 4\)

\(= 2a^2 b – 8b + a^2 – 4\)

\(= 2b (a^2 – 4) + (a^2 – 4) \)

\(= (a^2 – 4)(2b + 1) \)

\(= (a + 2)(a – 2)(2b + 1) \)

よって

\( \color{red}{(a + 2)(a – 2)(2b + 1)}\)

解答（順番に）：無理数、無理数、実数

実数は有理数と無理数に分類されます。有理数でない実数が無理数であり、この2つを合わせたものが実数の全体となります。

\(\sqrt{16} = 4\)（有理数）、\(-\displaystyle\frac{3}{4}\)（有理数）、\(0.5 = \displaystyle\frac{1}{2}\)（有理数）。

また、\(\sqrt{7}\) と \(\pi\) は循環しない無限小数より無理数であるから

b) \(\color{red}{\sqrt{7}}\)、d) \(\color{red}{\pi}\)

各数の近似値を求めると、

\(\sqrt{10} \fallingdotseq 3.16\)、\(3.2 = 3.2\)、\(\displaystyle\frac{10}{3} \fallingdotseq 3.33\)、\(\pi \fallingdotseq 3.14\)

したがって、

\(\color{red}{\pi < 3.2 < \sqrt{10} < \frac{10}{3}}\)

\(\sqrt{48} = \sqrt{16 \times 3} = \sqrt{16} \times \sqrt{3} = 4\sqrt{3}\)

したがって、

\(\color{red}{4\sqrt{3}}\)

\(\sqrt{2} – \sqrt{18} +\sqrt{32}\)

\(= \sqrt{2} – \sqrt{2 \cdot 3^2} +\sqrt{2 \cdot 4^2}\)

\(= \sqrt{2} – 3\sqrt{2} +4\sqrt{2}\)

\(= (1-3+4)\sqrt{2}\)

\(=2\sqrt{2}\)

よって

\( \color{red}{2\sqrt{2}}\)

\(\sqrt{5} \times \sqrt{10} \times \sqrt{45}\times \sqrt{40}\)

\(=\sqrt{5} \times \sqrt{10} \times 3\sqrt{5}\times 2\sqrt{10}\)

\(=(\sqrt{5})^2 \times (\sqrt{10})^2 \times 3 \times 2 \)

\(=5 \times 10 \times 3 \times 2 \)

\(=300\)

よって

\(\color{red}{300} \)

\(-\displaystyle\frac{1}{\sqrt{3}} + \sqrt{27} + \displaystyle\frac{4}{\sqrt{3}}\)

\(=-\displaystyle\frac{\sqrt{3}}{3} + 3\sqrt{3} +\displaystyle\frac{4\sqrt{3}}{3} \)

\(= \displaystyle\frac{-\sqrt{3}+9\sqrt{3} + 4\sqrt{3}}{3}\)

\(= \displaystyle\frac{12\sqrt{3}}{3}\)

\(= 4\sqrt{3}\)

よって

\( \color{red}{4\sqrt{3}}\)

\(\sqrt{98} + \sqrt{8} -\sqrt{50}\)

\(=7\sqrt{2} + 2\sqrt{2} -5\sqrt{2}\)

\(=4\sqrt{2} \)

よって

\(\color{red}{ 4\sqrt{2}}\)

\(\sqrt{7} \times \sqrt{21} \times \sqrt{12}\)

\(= \sqrt{7} \times \sqrt{7 \cdot 3} \times 2\sqrt{3}\)

\(= (\sqrt{7})^2 \times (\sqrt{3})^2 \times 2\)

\(= 7 \times 3 \times 2\)

\(= 42\)

よって

\(\color{red}{42}\)

\(\displaystyle\frac{3}{\sqrt{5}-2} \times \displaystyle\frac{\sqrt{5}+2}{\sqrt{5}+2} = \displaystyle\frac{3(\sqrt{5}+2)}{5-4}=3(\sqrt{5}+2)\)

したがって、

\(\color{red}{3(\sqrt{5}+2)}\)

\(\displaystyle\frac{3}{\sqrt{5} – \sqrt{2}} \times \displaystyle\frac{\sqrt{5} + \sqrt{2}}{\sqrt{5} + \sqrt{2}}\)

\(=\displaystyle\frac{3(\sqrt{5} + \sqrt{2})}{5 – 2}\)

\(= \sqrt{5} + \sqrt{2}\)

\(\displaystyle\frac{3}{\sqrt{5} + \sqrt{2}} \times \displaystyle\frac{\sqrt{5} – \sqrt{2}}{\sqrt{5} – \sqrt{2}}\)

\(=\displaystyle\frac{3(\sqrt{5} – \sqrt{2})}{5 – 2}\)

\(= \sqrt{5} – \sqrt{2}\)

よって

与式）

\( = (\sqrt{5} + \sqrt{2}) + (\sqrt{5} – \sqrt{2}) \)

\( = \color{red}{2\sqrt{5}}\)

\(\displaystyle\frac{2}{\sqrt{11} – 3}\)

\(= \displaystyle\frac{2}{\sqrt{11} – 3} \times \displaystyle\frac{\sqrt{11} + 3}{\sqrt{11} + 3}\)

\(= \displaystyle\frac{2(\sqrt{11} + 3)}{11 – 9}\)

\(= \sqrt{11} + 3\)

よって

（与式）

\(= (\sqrt{11} + 3) – \sqrt{11}\)

\(= \color{red}{3}\)

\(\displaystyle\frac{10}{\sqrt{15} + 5}\)

\(= \displaystyle\frac{10}{\sqrt{15} + 5} \times \displaystyle\frac{\sqrt{15} – 5}{\sqrt{15} – 5}\)

\(= \displaystyle\frac{10(\sqrt{15} – 5)}{15 – 25}\)

\(= – (\sqrt{15} – 5\)

\(= – \sqrt{15} + 5\)

よって

（与式）

\(= (- \sqrt{15} + 5) + \sqrt{15} \)

\(= \color{red}{5}\)

\(\sqrt{5}+1)^2=5+2\sqrt{5}+1=6+2\sqrt{5}\)

\(\sqrt{6+2\sqrt{5}}=\sqrt{5}+1\)

したがって、

\(\color{red}{\sqrt{5}+1}\)

\(x=2\) を代入すると

\(2^2-3(2)+1=4-6+1=-1\)

したがって、

\(\color{red}{-1}\)

\(x=1+\sqrt{2}\)より

\(x-1=\sqrt{2}\)であるから、両辺を２乗すると

\((x-1)^2=2\)、すなわち \(x^2-2x+1=2\)

したがって、これを整理すると

\(\color{red}{x^2-2x-1=0}\)

\(a^2+b^2=(a+b)^2-2ab=5^2-2(6)=25-12=13\)

したがって、

\(\color{red}{13}\)

\((x+\displaystyle\frac{1}{x})^2=x^2+2+\displaystyle\frac{1}{x^2}=9\) より

\(x^2+\displaystyle\frac{1}{x^2}=9-2=7\)

したがって、

\(\color{red}{7}\)

\(2x > 8\) より \(\color{red}{x > 4}\)

\(-3x \leq 6\) より

\(\color{red}{x \geq -2}\)（不等号の向きが変わる）

\(2x + 1 > 9\) を解くと

\(x > 4 \) ……①

\(3x + 5 \leq 32\)を解くと

 \(x \leq 9\) ……②

①、②より

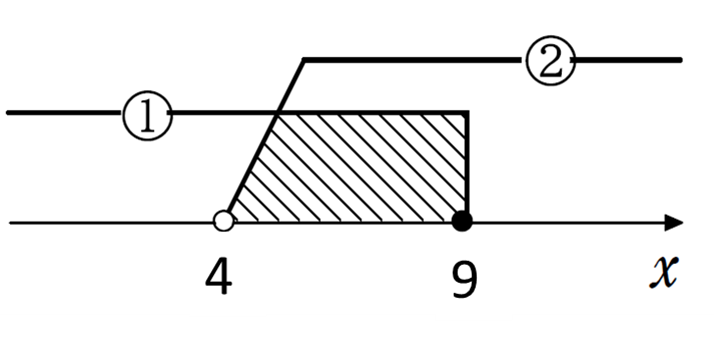
\(\color{red}{4 < x \leq 9}\)

⇔　\(\begin{eqnarray}
\left\{
\begin{array}{l}
2x – 1 < 3x \\
3x < – x + 8
\end{array}
\right.
\end{eqnarray}\)

⇔　
\(2x – 1 < 3x\) を解くと\(-1 < x\) 　…①
\(3x < -x + 8\) を解くと\(x < 2\) 　 …②
①、②より
\(\color{red}{-1 < x < 2} \)

\(x-3=5\)または\(x-3=-5\)より

\(\color{red}{x=-2 , 8}\)

\(-3 < x+1 < 3\) より

\(\color{red}{-4 < x < 2}\)

\(2x-3 \geq 1\)または\(2x-3 \leq -1\)より

\(\color{red}{x \geq 2またはx \leq 1}\)