- 因数分解とは
- 共通因数のくくり出し
- 因数分解の公式
- 複雑な因数分解のコツ
因数分解とは、簡潔にいえば、「展開の逆」になります。
\((x + 3) (x – 2) \) は展開すると，\(x^2 + x – 6\) になりますが，逆に，\(x^2 + x – 6\) は \((x + 3 ) (x – 2) \) に変形することができます。
このように，多項式を積の形に表すことを因数分解するといいます。
また、このときの積を作っている各多項式のことを因数といいます。
因数分解とは～共通因数のくくり出しのやり方～
共通因数のくくり出しとは、多項式の分配法則
\(A(B + C) = AB + AC , (A + B)C = AC + BC\)
の逆になります。
すなわち，各項に共通な因数（文字や数字）があれば、以下のようにくくり出しを行うことができます。
\(AB + AC = A (B+C) \)
例題
次の式を因数分解せよ。
\(3a^3b-9a^2b^2 \)
解答
\(3a^3b-9a^2b^2 = 3a^2b(a-3b)\)
シンスケ因数分解をするときは、まずは共通因数のくくり出しができないか考えることがとても大切な事項となります。
因数分解とは～公式～
基本的な展開公式の逆を考えることで、以下の因数分解の公式が得られます。
① \(a^2 + 2ab + b^2 = (a+b)^2 , a^2 – 2ab + b^2 = (a-b)^2 \)
② \(a^2 – b^2 = (a+b) (a-b) \)
③ \( x^2 + (a+b) x + ab = (x+a) (x+b)\)
④ \( acx^2 + (ad+bc) x + bd=(ax+b) (cx+d)\) ※たすきがけ
例題
次の式を因数分解せよ。
① \(x^2 + 12xy + 36y^2\)
② \(25a^2 – 9b^2 \)
③ \(x^2 +6x +5 \)
④ \( 8x^2-51x+18 \)
解答
① \(x^2 + 12xy + 36y^2\)
\(= x^2 + 2 \cdot x \cdot 6y + (6y)^2\)
\(=(x+6)^2 \)
② \(25a^2 – 9b^2 \)
\(=(5a)^2 – (3b)^2\)
\(= (5a+3b) (5a-3b) \)
③ \(x^2 +6x +5 \)
\(= x^2 + (1+5) x + 1 \cdot 5\)
\( = (x+1) (x+5)\)
④ \( 8x^2-51x+18\)
\(= (x-6) (8x-3)\)
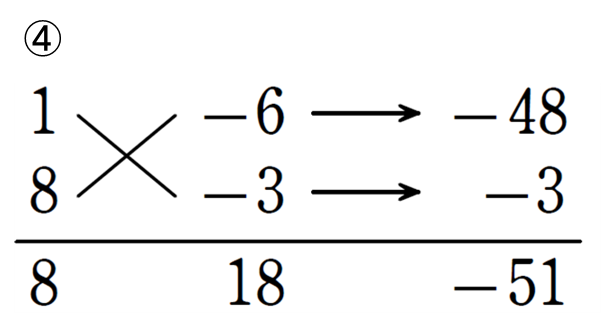
上記の④のような計算方法をたすき掛けといいます。
因数分解とは～複雑な因数分解のやり方～
複雑な多項式は式の形の特徴に着目し、工夫することで因数分解をすることができます。
部分的な因数分解
多項式全体では因数分解できないときも、部分的に因数分解していくことで最終的に因数分解できることがあります。
また、共通因数があるときは必ず最初にくくり出しを行いましょう。
例題
次の式を因数分解せよ。
\(ax^2 – 6ax + 9a – ay^2\)
解答
\(ax^2 – 6ax + 9a – ay^2\) ⇐ まずは、全体の共通因数 \(a\) でくくり出しを行う
\(= a(x^2 – 6x + 9 – y^2)\) ⇐ \(x^2 – 6x + 9\) の部分が因数分解できる
\(= a\{(x – 3)^2 – y^2\}\) ⇐ \(x – 3\) を１つの文字の塊と考えて因数分解
\(= a\{(x – 3) + y\} \{(x – 3) – y \}\) ⇐ \(A^2 – B^2 = (A + B) (A – B)\)
\(= a(x + y – 3) (x – y -3) \) ⇐ 中カッコは必ず外す
シンスケ部分的に因数分解できる箇所を見逃さないことがポイントです。
文字の置き換え
文字の置き換えをすることで、通常の因数分解の公式が利用できる形にもっていくことができることがあります。
例題
次の式を因数分解せよ。
\(x^4 – 13x^2 – 48\)
解答
\(x^4 – 6x^2 – 27\) ⇐ \(x^4 = (x^2)^2\) とみる
\(= (x^2)^2 – 6(x^2) – 27\) ⇐ \(x^2\) を１つの文字\(A\)と考える
\(= \{(x^2) + 3\} \{(x^2) – 9\}\) ⇐ \(A^2 – 6 A + 27 = (A + 3) (A – 9)\)
\(= (x^2 + 3) (x + 3) (x – 3) \) ⇐ 因数分解できる部分は残さない
シンスケ因数分解できる部分は残さないように最後まで注意しましょう。
降べきの順に整理
２種類以上の文字を含み、かつ、一見して部分的にも因数分解ができないときは、次数の低い文字について降べきの順に整理することで因数分解の公式が利用できる形にもっていくことができます。
例題
次の式を因数分解せよ。
\(a^2b + a^2 – b – 1\)
解答
\(a^2b + a^2 – b – 1\) ⇐ 次数の低い文字 \(b\) について降べきの順に整理
\(= (a^2 -1) b + (a^2 – 1)\) ⇐ 共通因数 \(a^2 – 1)\) でくくり出す
\(= (a^2 – 1) (b + 1) \) ⇐ \(a^2 – 1\) はまだ因数分解できる
\(= (a + 1)(a – 1)(b + 1)\) ⇐ 因数分解できる部分は残さない
💬 今回の解説を読んで「まだ少し不安」「一人だと解き直せない」と感じた方へ
数学は「解説を読んで理解した気になって終わり」にしてしまうと、似た問題が出たときに手が止まってしまいがちです。
確実に定着させるには、知識が新しいうちに自分で解き直し、類題で練習することが欠かせません。
もし「テキストの解説だけだと理解に時間がかかる」「質問できる環境や、手厚いサポートが欲しい」と感じている場合は、高校生向けの学習サービスを上手に活用するのも手です。
特に「わかりやすい動画解説でつまずきを解消できる（スタディサプリ）」や、「自分のレベルに合わせて添削・演習ができる（進研ゼミ）」は、独学の強い味方になります。
自分の学習スタイルに合う方法を見つけたい方は、以下の記事を参考にしてみてください。🔹 人気の2大教材（動画授業 vs 演習・添削）を比較して選びたい方
👉 【高校生向け】進研ゼミとスタディサプリはどっちがおすすめ？特徴と料金の違い🔹 他社も含めたおすすめ通信教育を幅広くチェックしたい方
👉 【高校生向け】通信教育おすすめランキング！人気教材を徹底比較
コメント