ここでは、【数学II】「微分法・積分法」でよく利用する公式（基礎知識）や例題を一覧にしてまとめています。
微分法〜基本公式・例題一覧〜
１．微分係数
関数\(f(x)\) において，\(x\) が\(a\) から\(b\)まで変化するときの平均変化率は
\(\displaystyle \color{red}{\displaystyle\frac{f(b) – f(a)}{b – a}}\)
※平均変化率は中学における「変化の割合」と同じ
例題
\(y = x^2\) において \(x\) が \(a\) から \(b\) まで変化するときの平均変化率を求めよ。
解答
\(x\) が \(a\) から \(b\) まで変化するとき, \(y\) が \(a^2\) から \(b^2\) まで変化するので
\(\displaystyle\frac{b^2 – a^2}{b – a}\)
\(= \displaystyle\frac{(b + a)(b – a)}{b – a}\)
\(= a + b\)
関数\(f(x)\) の\(x = a\) における微分係数\(f’(a)\)は
\(\displaystyle \color{red}{f’(a) = \lim\limits_{h \to 0}\displaystyle\frac{f(a+h) – f(a)}{h}}\)
※微分係数\(f’(a)\) は「関数\(y = f(x)\)の\(x = a\)における接線の傾き」を表す
例題
\(f(x) = x^2\) の\(x = 3\) における微分係数を求めよ。
解答
\(f’(3) = \lim\limits_{h \to 0}\displaystyle\frac{f(3 + h) – f(3)}{h}\)
\(= \lim\limits_{h \to 0}\displaystyle\frac{(3 + h)^2 – 3^2}{h}\)
\(= \lim\limits_{h \to 0}\displaystyle\frac{6h + h^2}{h}\)
\(= \lim\limits_{h \to 0}(6 + h) = 6\)
２．導関数
\(\displaystyle \color{red}{f’(x) = \lim\limits_{h \to 0}\displaystyle\frac{f(x+h) – f(x)}{h}}\)
※導関数\(f’(x)\) は「接線の傾きが出る式」を表す
例題
\(f(x) = x^2\) の導関数を求めよ。
解答
\(f’(x) = \lim\limits_{h \to 0}\displaystyle\frac{f(x+h) – f(x)}{h}\)
\(= \lim\limits_{h \to 0}\displaystyle\frac{(x + h)^2 – x^2}{h}\)
\(= \lim\limits_{h \to 0}\displaystyle\frac{(x^2 + 2hx + h^2) – x^2}{h}\)
\(= \lim\limits_{h \to 0}\displaystyle\frac{2hx + h^2}{h}\)
\(= \lim\limits_{h \to 0}(2x + h)\)
\(= 2x\)
\(n\)を正の整数、\(c\)を定数とするとき、
・\((x^n)’ = nx^{n-1}\)
・\((c)’ = 0 \)
例題
次の関数の導関数を求めよ。
（１）\(f(x) = x^3\)
（２）\(f(x) = 5\)
解答
（１）\(f'(x) = (x^3)’ = 3x^{3-1} = 3x^2\)
（２）\(f'(x) = (5)’ = 0 \)
\(k, l\) は定数とするとき、
- \(\{kf(x)\}’ = kf’(x)\)
- \(\{f(x) + g(x)\}’ = f’(x) + g’(x)\)
- \(\{kf(x) + lg(x)\}’ = kf’(x) + lg’(x)\)
例題
次の関数を\(x\) について微分せよ。
（１）\(f(x) = 2x^3\)
（２）\(f(x) = x^3 + x^2\)
（３）\(f(x) = x^3 – 2x^2 + 5x -1\)
解答
（１）\(f'(x) = 2(x^3)’ = 2 \cdot 3x^2 = 6x^2\)
（２）\(f'(x) = (x^3)’ + (x^2)’ = 3x^2 + 2x\)
（３）\(f'(x) = (x^3)’ – 2(x^2)’ + 5(x)’ – (1)’\)
\(= 3x^2 – 2 \cdot 2x + 5 \cdot 1 – 0\)
\(= 3x^2 – 4x + 5 \)
３．接線の方程式
曲線\(y = f(x)\)上の点\(A(a, f(a)) における接線の方程式は
\(\displaystyle \color{red}{y – f(a) = f’(a)(x – a)}\)
例題
曲線 \(f(x) = x^2 – 2x + 3\) 上の点\((3, 6)\) における接線の方程式を求めよ。
解答
\(f'(x) = 2x – 2\) より
\(f'(3) = 2 \cdot 3 – 2 = 4\)
したがって，
\(y – 6 = 4 (x – 3)\)
\(y = 4x – 6\)
４．関数の増減
関数\(y = f(x)\)において
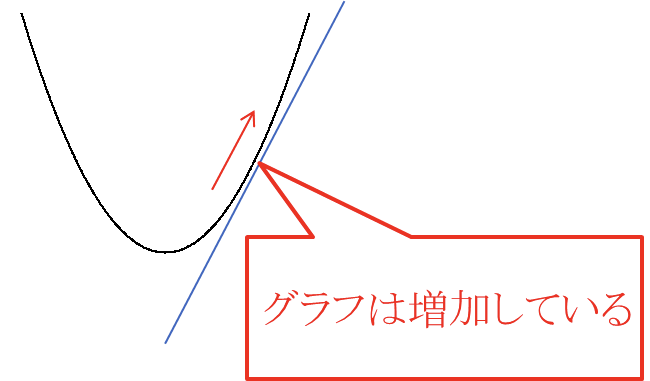
①\(f’(x) > 0\) となる\(x\) の値の範囲ではグラフは増加する
※接線の傾きが正の範囲ではグラフは増加する
②\(f’(x) < 0\) となる\(x\) の値の範囲ではグラフは減少する
※接線の傾きが負の範囲ではグラフは減少する
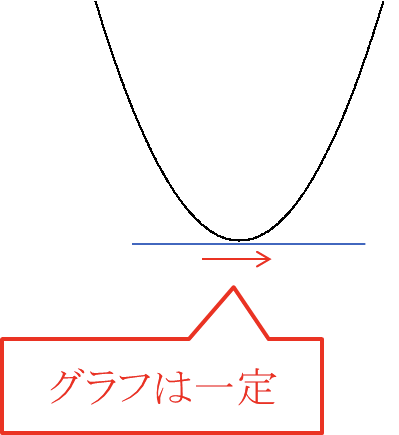
③\(f’(x) = 0\) となる\(x\) の値の範囲ではグラフは一定
※接線の傾きが0の部分ではグラフは一定となる
例題
関数\(f(x) = x^3 + 3x^2 -2\) の増減を調べよ。
解答
\(f'(x) = 3x^2 + 6x = 0\) を解くと
\(3x(x + 2) = 0\)
\(x = -2, 0\)
| \(x\) | \(\cdots\) | \(-2\) | \(\cdots\) | \(0\) | \(\cdots\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | ↗︎ | \(2\) | ↘︎ | \(-2\) | ↗︎ |
したがって，上記の増減表より，
\(x \leq -2, 0 \leq x\) のとき，増加する
\(-2 \leq x \leq 0\) のとき，減少する
５．関数の極大・極小
関数\(y = f(x)\) について
①\(f’(x)\) の符号が\(x = a\)の前後で正から負に変わるとき、
\(f(x)\)は\(x = a\)で極大になるといい、\(f(a)\)を極大値という
②\(f’(x)\) の符号が\(x = a\)の前後で負から正に変わるとき、
\(f(x)\)は\(x = a\)で極小になるといい、\(f(a)\)を極小値という
※極大値と極小値をまとめて、「極値」という。
例題
関数\(f(x) = x^3 – 3x^2 – 9x – 2\) の極値を求めよ。
解答
\(f'(x) = 3x^2 – 6x – 9 = 0\) を解くと
\(3(x^2 – 2x – 3) = 0\)
\(3(x +1)(x – 3) = 0\)
\(x = -1, 3\)
| \(x\) | \(\cdots\) | \(-1\) | \(\cdots\) | \(3\) | \(\cdots\) |
| \(f'(x)\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(f(x)\) | ↗︎ | \(3\) | ↘︎ | \(-29\) | ↗︎ |
したがって、
\(x = -1\) のとき 極大値\(3\)
\(x = 3\) のとき 極小値\(-29\)
関数\(f(x)\)が\(x = a\)で極値をとるとき、\(f’(a) = 0\)
※ただし、\(f’(a) = 0\)であっても、関数\(f(x)\)は\(x = a\)で極値をとるとは限らない
例題
関数\(f(x) = x^3\) において，極値があればそれを求めよ。
解答
\(f'(x) = 3x^2 = 0\) を解くと
\(x = 0\)
| \(x\) | \(\cdots\) | \(0\) | \(\cdots\) |
| \(f'(x)\) | \(+\) | \(0\) | \(+\) |
| \(f(x)\) | ↗︎ | \(0\) | ↗︎ |
上記のように，\(x = 0\) は\(f'(x) = 0 \) となる唯一の点であるが，極値ではない。
したがって、極値はない
積分法〜基本公式・面積公式・例題一覧〜
１．不定積分
\(F’(x) = f(x)\) のとき
\(\int f(x) dx = F(x) + C\) (\(C\) は積分定数)
※\(F(x)\)を原始関数という
\(\int x^n dx = \displaystyle\frac{1}{n+1}x^{n+1} + C\) (\(C\) は積分定数)
※特に，\(\int 1 dx\) すなわち\(\int dx = x + C\)
例題
次の不定積分を求めよ。ただし，積分定数は\(C\) とせよ。
（１）\(\int x^2 dx\)
（２）\(\int x dx \)
解答
（１）\(\int x^2 dx = \displaystyle\frac{1}{2+1}x^{2+1} + C = \displaystyle\frac{1}{3}x^{3} + C\)
（２）\(\int x dx = \displaystyle\frac{1}{1+1}x^{1+1} + C = \displaystyle\frac{1}{2}x^{2} + C\)
\(k, l\) は定数とする
①\(\int kf(x) dx = k \int f(x) dx \)
②\(\int \{f(x) + g(x)\} dx = \int f(x) dx + \int g(x) dx \)
③\(\int \{kf(x) + lg(x)\} dx = k\int f(x) dx + l\int g(x) dx \)
例題
（１）\(\int 6x^2 dx\)
（２）\(\int (x^2 + x) dx\)
（３）\(\int (3x^2 – 4x + 2 ) dx\)
解答
（１）\(\int 6x^2 dx = 6 \int x^2 dx \)
\(= 6 \cdot \displaystyle\frac{1}{3} x^3dx\)
\(= 2 x^3dx + C\)
（２）\(\int \{x^2 + x\} dx = \int x^2 dx + \int x dx \)
\(= \displaystyle\frac{1}{3} x^3 + \displaystyle\frac{1}{2} x^2 + C \)
（３）\(\int \{3x^2 – 4x + 2 \} dx = 3\int x^2 dx – 4\int x dx + \int 2 dx\)
\(= 3 \cdot \displaystyle\frac{1}{3} x^3 – 4 \cdot \displaystyle\frac{1}{2} x^2 + 2x + C\)
\(= x^3 – 2x^2 + 2x + C\)
２．定積分
\(F’(x) = f(x)\) のとき
\(\int_{a}^{b} f(x) dx = \left[F(x)\right]_{a}^{b} = F(b) – F(a) \)
例題
\(\int_{1}^{2} x^2 dx\) を計算せよ。
解答
\(\int_{1}^{2} x^2 dx = \left[ \displaystyle\frac{1}{3}x^3\right]_{1}^{2} \)
\(= \displaystyle\frac{1}{3} \cdot 2^3 – \displaystyle\frac{1}{3} \cdot 1^3\)
\(= \displaystyle\frac{8}{3} – \displaystyle\frac{1}{3} \)
\(= \displaystyle\frac{7}{3}\)
\(k\) は定数とする
①\(\int_{a}^{b} kf(x) dx = k \int_{a}^{b} f(x) dx \)
②\(\int_{a}^{b} \{f(x) + g(x)\} dx = \int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx \)
③\(\int_{a}^{a} f(x) dx = 0\)
④\(-\int_{a}^{b} f(x) dx = \int_{b}^{a} f(x) dx\)
⑤\(\int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx = \int_{a}^{b} f(x) dx\)
例題
（１）\(\int_{1}^{2} x^2 dx\) を計算せよ。
（２）\(\int_{0}^{1} x dx – \int_{2}^{1} x dx\) を計算せよ。
解答
（１）\(\int_{0}^{1} (3x^2 – 4x) dx = \left[ x^3 – 2x^2 \right]_{0}^{1}\)
\(= (1^3 – 2 \cdot 1^2) – (0^3 – 2 \cdot 0^2) \)
\(= -1\)
（２）\(\int_{0}^{1} x dx – \int_{2}^{1} x dx\)
\(= \int_{0}^{1} x dx + \int_{1}^{2} x dx\) ←性質④を利用
\(= \int_{0}^{2} x dx\) ←性質⑤を利用
\(= \left[ \displaystyle\frac{1}{2}x^2 \right]_{0}^{2}\)
\(= \displaystyle\frac{1}{2} \cdot 2^2\)
\(= 2\)
３．定積分と微分法
\(\displaystyle \color{red}{\displaystyle\frac{d}{dx}\int_{a}^{x} f(t) dt = f(x)}\) (\(a\)は定数)
例題
\(\displaystyle\frac{d}{dx}\int_{1}^{x} (2t^2 – t + 3) dt\) を計算せよ。
解答
\(2x^2 – x + 3\)
４．面積
区間 \(a\leq x \leq b\) において
\(f(x) \geq 0\) のとき \(\displaystyle \color{red}{S = \int_{a}^{b}f(x)dx}\)
\(f(x) \leq 0\) のとき \(\displaystyle \color{red}{S = \int_{a}^{b}\{-f(x)\}dx}\)
例題
放物線 \(y = x^2 + 3\) と \(x\) 軸，および \(2\) 直線 \(x = -1, x = 3\) で囲まれた図形の面積\(S\) を求めよ。
解答
\(S = \int_{-1}^{3}(x^2 + 3) dx\)
\(= \left[ \displaystyle\frac{1}{3}x^3 + 3x \right]_{-1}^{3}\)
\(= (9 + 9) – \left(-\displaystyle\frac{1}{3} – 3\right) \)
\(= \displaystyle\frac{64}{3}\)
区間 \(a\leq x \leq b\)で\(f(x) \geq g(x)\) のとき
\(\displaystyle \color{red}{S = \int_{a}^{b}\{f(x) – g(x) \}dx}\)
例題
次の2つの放物線で囲まれた図形の面積\(S\) をもとめよ。
\(y = x^2 + x – 3, y = – x^2 – 3x + 3 \)
解答
2つの放物線の交点を求めると
\(x^2 + x – 3 = – x^2 – 3x + 3 \)
の解である。これを解くと
\(2x^2 + 4x – 6 = 0\)
\(2(x + 3)(x – 1)= 0\)
\(x = -3, 1\)
よって、求める面積\(S\) は
\(S = \int_{-3}^{1}\{(-x^2 -3x + 3) – (x^2 + x – 3)\} dx\)
\(= \int_{-3}^{1}\{(-2x^2 -4x + 6)\} dx\)
\(= \displaystyle\frac{64}{3}\)
５．面積公式
\(y = f(x)\) において
①\(f(x)\)が奇関数のとき
\(\displaystyle \color{red}{\int_{-a}^{a} f(x) dx = 0}\)
②\(f(x)\)が偶関数のとき
\(\displaystyle \color{red}{\int_{-a}^{a} f(x) dx = 2\int_{0}^{a} f(x) dx} \)
例題
次の値を求めよ。
（１）\(\int_{-2}^{2}x^3 dx\)
（２）\(\int_{-1}^{1}x^2 dx\)
解答
（１）\(\int_{-2}^{2}x^3 dx\)
\(y = x^3\) は奇関数より，
\(\int_{-2}^{2}x^3 dx\)
\(= 0\)
（２）\(\int_{-1}^{1}x^2 dx\)
\(y = x^2\) は偶関数より，
\(\int_{-1}^{1}x^2 dx\)
\(= 2\int_{0}^{1}x^2 dx\)
\(= 2\left[ \displaystyle\frac{1}{3}x^3 \right]_{0}^{1}\)
\(= 2 \cdot \displaystyle\frac{1}{3}\)
\(= \displaystyle\frac{2}{3}\)
\(\displaystyle \color{red}{\int_{\alpha}^{\beta}(x – \alpha)(x – \beta)dx = -\displaystyle\frac{1}{6}(\beta – \alpha)^3 }\)
\(\displaystyle \color{red}{\int_{\alpha}^{\beta}(x – \alpha)^2 dx = \displaystyle\frac{1}{3}(\beta – \alpha)^3 }\)
例題
次の計算をせよ。
（１）\( \displaystyle\int_{-1}^{3}(x + 1)(x – 3)dx\)
（２）\( \displaystyle\int_{-5}^{3}(x + 5)^2dx\)
解答
（１）\(\displaystyle\int_{-1}^{3}(x + 1)(x – 3)dx= -\displaystyle\frac{1}{6}(3 – (-1))^3\)
\(= -\displaystyle\frac{32}{3}\)
（２）\( \displaystyle\int_{-5}^{3}(x + 5)^2dx = \displaystyle\frac{1}{3}(3 + 5)^3\)
\(=\displaystyle\frac{512}{3}\)
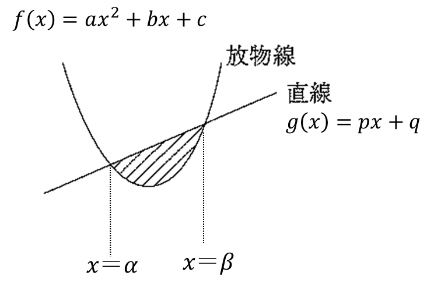
放物線 \( f(x) = ax^2+ bx + c\) と直線 \(g(x) = px+q\) の交点の \(x\) 座標を \(α, β(α<β）\)とするとき，この放物線と直線で囲まれた図形の面積 \(S\) は
\(\displaystyle \color{red}{S = \displaystyle\frac{|a|}{6}(\beta – \alpha)^3}\)
例題
次の放物線と直線で囲まれた図形の面積\(S\) をもとめよ。
\(y = -x^2 + 3x +2 , y = x – 1 \)
解答
2つの放物線の交点を求めると
\(-x^2 + 3x + 2 = x – 1 \)
の解より，\(x = -1, 3\)
よって、求める面積\(S\) は
\(S = \displaystyle\frac{|-1|}{6}(3 – (-1))^3\)
\(= \displaystyle\frac{32}{3}\)
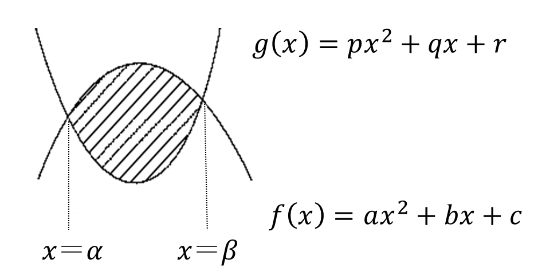
放物線 \( f(x) = ax^2+ bx + c\) と直線 \(g(x) = px^2+qx+r\) の交点の \(x\) 座標を \(α, β(α<β）\)とするとき，この2つの放物線で囲まれた図形の面積 \(S\) は
\(\displaystyle \color{red}{S = \displaystyle\frac{|a – p|}{6}(\beta – \alpha)^3}\)
例題
次の2つの放物線で囲まれた図形の面積\(S\) をもとめよ。
\(y = x^2 + x – 3, y = – x^2 – 3x + 3 \)
解答
2つの放物線の交点を求めると
\(x^2 + x – 3 = – x^2 – 3x + 3 \)
の解より，\(x = -3, 1\)
よって、求める面積\(S\) は
\(S = \displaystyle\frac{|1 – (-1)|}{6}(1 – (-3))^3\)
\(= \displaystyle\frac{64}{3}\)
放物線 \( f(x) = ax^2+ bx + c\) とその接線 \(g(x) = px+q\) の接点の \(x\) 座標を \(α\)とするとき，この放物線と接線および直線\(x = \beta\) で囲まれた図形の面積 \(S\) は
\(\displaystyle \color{red}{S = \displaystyle\frac{|a|}{3}(\beta – \alpha)^3}\)
例題
放物線\(y = -x^2 – 4x -34\) を\(C\) , \(C\) 上の点\(A(-5, -39)\) における接線を\(\ell\) とする。
直線\(x = 3\) と放物線\(C\) および直線\(\ell\) で囲まれた図形の面積\(S\) を求めよ。
解答
\(f(x) = -x^2 – 4x – 3\) とおく
\(f'(x) = – 2x – 4\)
\(f'(-5) = 6\)
よって，接線の方程式は\((-5, -39)\) を通り，傾き\(6\) より
\(y + 39 = 6(x + 5)\)
\(y = 6x – 9\)
よって、求める面積\(S\) は
\(S = \displaystyle\frac{|-1|}{3}(3 – (-5))^3\)
\(= \displaystyle\frac{512}{3}\)
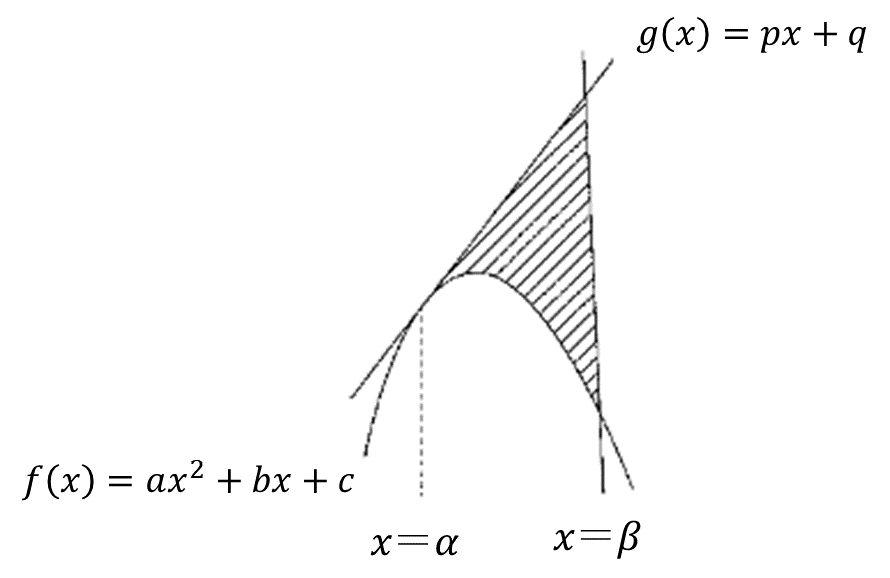
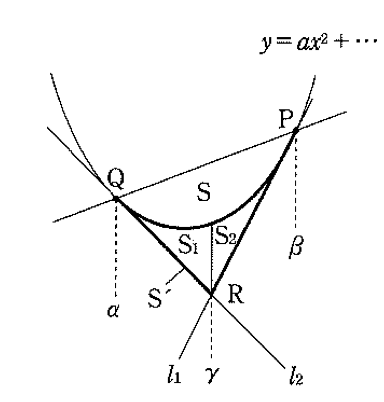
図において，放物線 \( y = ax^2 + bx + c \) と2本の接線の接点\(Q\),\(P\)の \(x\) 座標をそれぞれ \( \alpha, \beta \)(\( \alpha < \beta \))とすると，
① \(\displaystyle \color{red}{r = \displaystyle\frac{\alpha + \beta}{2}}\)
② \(\displaystyle \color{red}{S = \displaystyle\frac{|a|}{6}(\beta – \alpha)^3}\)
③ \(\displaystyle \color{red}{S’ = S_1 + S_2 = \displaystyle\frac{|a|}{12}(\beta – \alpha)^3}\)
④ \(\displaystyle \color{red}{S_1 = S_2 = \displaystyle\frac{|a|}{24}(\beta – \alpha)^3}\)
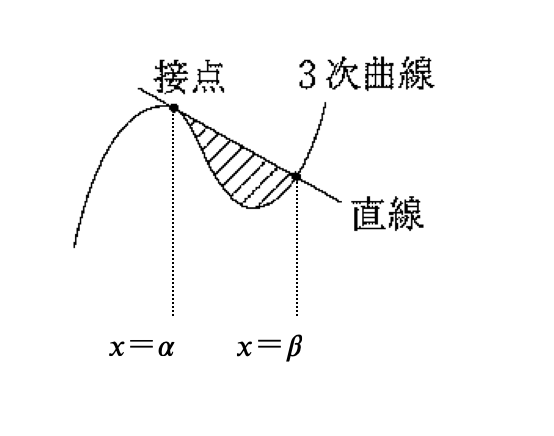
3次関数 \( y = f(x) \)（3次の係数が \( a \)）とその接線 \( y = g(x) \) が，\( x = \alpha \) で接し，\( x = \beta \) で交わるとき，この3次関数と接線で囲まれた図形の面積 \( S \) は
\( \displaystyle \color{red}{ S = \frac{ |a| }{ 12 } ( \beta – \alpha)^4 } \)
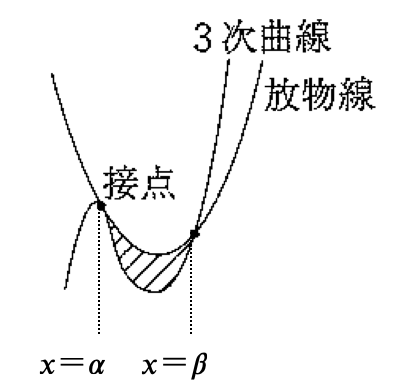
また、3次関数 \( y = f(x) \)（3次の係数が \( a \)）と2次関数 \( y = g(x) \) が，\( x = \\alpha \) で接し，\( x = \beta \) で交わるとき，この3次関数と接線で囲まれた図形の面積 \( S \) は
\( \displaystyle \color{red}{ S = \frac{ |a| }{ 12 } ( \beta – \alpha)^4 } \)
例題
曲線\(C : y = x^3 – 2x\) とその上の点\((1, -1)\) における接線とで囲まれた面積\(S\) を求めよ。
解答
\(f(x) = x^3 – 2x\) とおく
\(f'(x) = 3x^2 -2\)
\(f'(1) = 1\)
よって，接線の方程式は
\(y + 1 = x – 1\) より \(y = x -2\)
曲線\(C : y = x^3 – 2x\) と直線\(x -2\) の交点の\(x\) 座標は
\(x^3 -2x = x – 2\)
を解くと
\(x^3 -3x + 2 = 0\)
\((x – 1)^2(x+2) = 0\)
より
\(x = -2, 1\)
したがって、
\(S = \displaystyle\frac{|1|}{12}\{1 – (-2)\}^4\)
\(= \displaystyle\frac{27}{4}\)
コメント