 ラッシーくん
ラッシーくん二項定理がまったくわからないのですが、これだけは知っておいた方がいい知識や公式などはありますか?
このような疑問や悩みに答えます。



中学高校の数学教諭として15年以上現場で教えています。
- 二項定理とは?
- 二項定理の公式の導き方
- 二項定理を利用した応用問題例
二項定理は数学Ⅱの「式と計算」の1分野で扱われる内容ですが、苦手な方が多い印象です。
ここでは、二項定理の内容について、わかりやすく解説していきます。
二項定理とは?
二項定理とは?
そもそも二項定理とは物凄く簡単にいうと展開公式の一種と考えるとわかりやすいかと思います。



いやいや、展開公式くらいわかりますよ
このような人も多いかと思います。
中学や高校1年でやる展開公式には例えば以下のようなものがありましたね。
- \((a+b)(a-b)=a^2-b^2\)
- \((x+a)(x+b)=x^2+(a+b)x+ab\)
- \((a+b)^2=a^2+2ab+b^2\)
- \((a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca\)
- \((a+b)^3=a^3+3a^2b+3ab^2+b^3\)
上記を使えば、例えば、
\((x+2)^2=x^2+4x+4\)
\((x+2)^3=x^3+6x^2+12x+8\)
のように計算することができるかと思います。
しかしながら、2乗や3乗までなら公式で対応できるかと思いますが、
\((x+2)^4\), \((x+2)^5\), \((x+2)^6\),……
のような4乗、5乗、6乗、……といった高次の展開になると今までの公式が使いにくいため、これまでの知識だと簡単には展開することができないかと思います。
このようなときに
「このような高次の展開公式も規則的に計算できるよ~」
という法則が二項定理となります。



要するに、高次の展開を規則的にできる公式が二項定理だと考えるとよいでしょう。
まずは\((a+b)^3\)の公式の意味を理解しよう
実際に二項定理の公式を理解するために、まずは、\((a+b)^3\)の公式の意味を理解しましょう。
上記でもやりましたが、
\((a+b)^3=a^3+3a^2b+3ab^2+b^3\)
でしたね。
そもそも、これはどのように導かれるかというと、
\((a+b)^3=(a+b)(a+b)(a+b)\)
より、これを分配法則で展開して整理すると導くことができます。
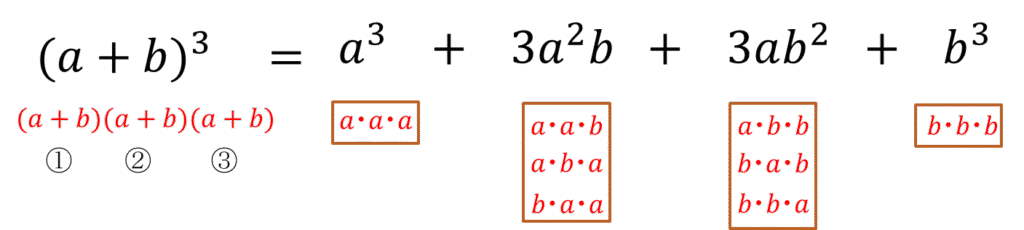
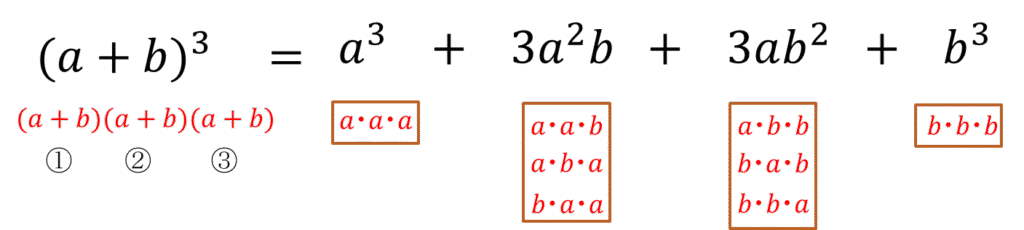
上記の①~③の\((a+b)\)の分配法則の組み合わせを考えると、具体的には
\(a×a×a\) で \(a^3\) の項が1つ
\(a×a×b\) , \(a×b×a\) , \(b×a×a\)で\(a^2b\)の項が3つ
\(a×b×b\) , \(b×a×b\) , \(b×b×a\) で \(ab^2\) の項が3つ
\(b×b×b\) で \(b^3\) の項が1つ
このような項が出てくるため、実際に
\((a+b)^3=a^3+3a^2b+3ab^2+b^3\)
が成り立ちます。
さて、ここで、上記の項の数について考えてみましょう。
例えば、上記の中で
\(a×a×b\) , \(a×b×a\) , \(b×a×a\) で \(a^2b\) の項が3つ
となりましたが、これはaabの並び方の総数になっていることがわかるかと思います。
これは数学A「場合の数」で扱っている同じものを含む順列の考え方により、以下で計算をすることができます。
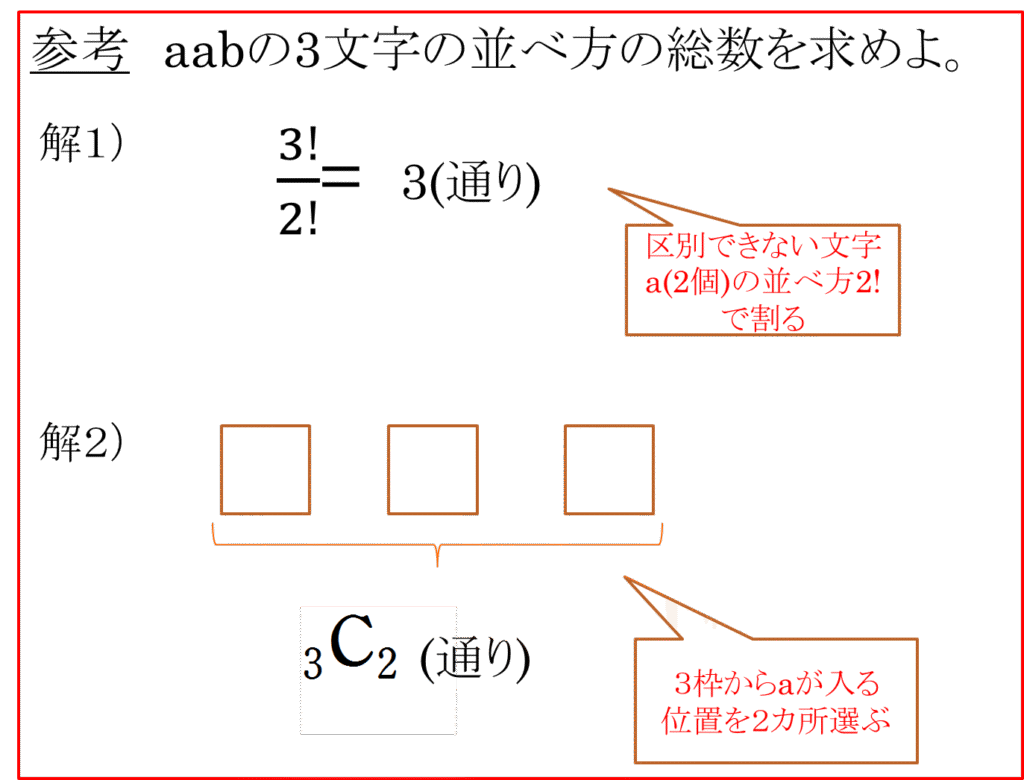

上記のように、2通りのやり方がありますが、ここでは解2)のやり方で考えると以下のように項の数を計算することができます。
\(a^3\)の項の数 → \({}_3 \mathrm{ C }_3 =1 \)で1つ
\(a^2b\)の項の数 → \({}_3 \mathrm{ C }_2 =3 \)で3つ
\(ab^2\) の項の数 → \({}_3 \mathrm{ C }_1 =3 \)で3つ
\(b^3\)の項の数 → \({}_3 \mathrm{ C }_0 =1 \)で1つ
したがって、\((a+b)^3\)の計算は以下のように表すことができます。
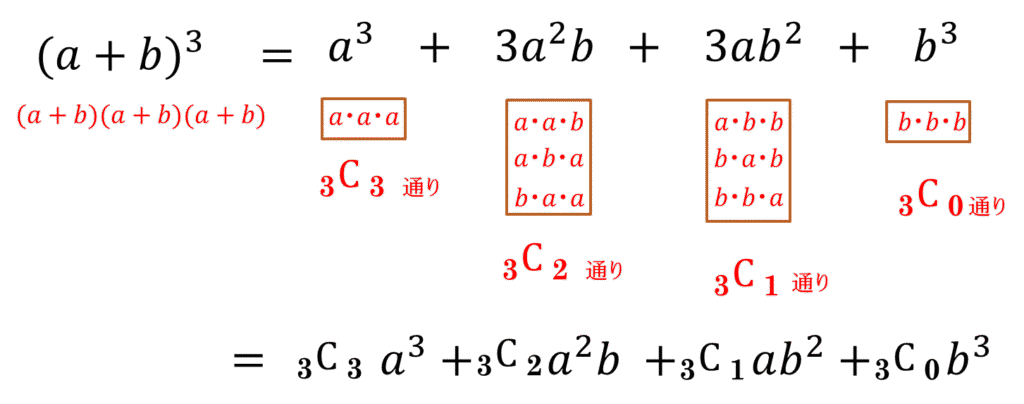
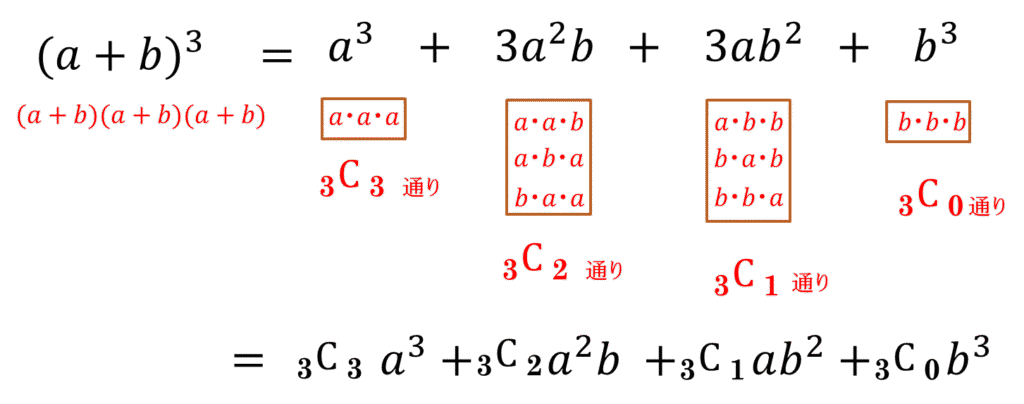
\((a+b)^3\)の公式から二項定理を導こう
\((a+b)^3\)と同様の計算規則で\((a+b)^4\)や、\((x-2)^5\)といった4乗、5乗の展開も以下のように計算できるようになります。
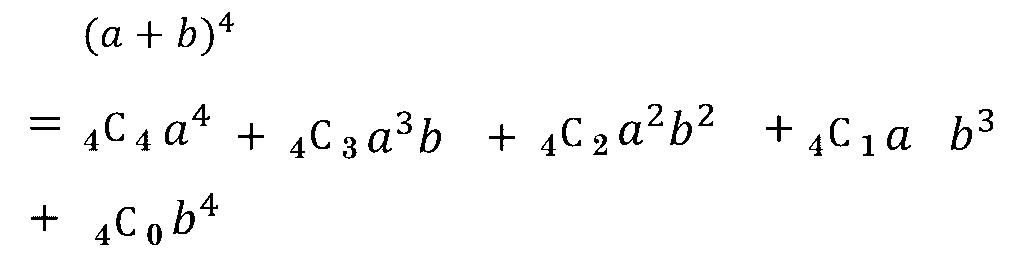
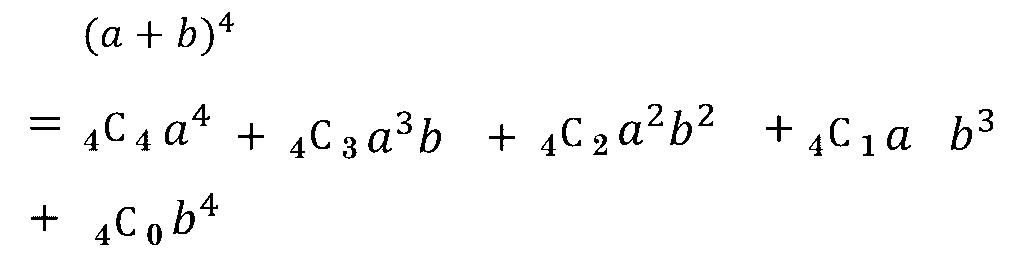
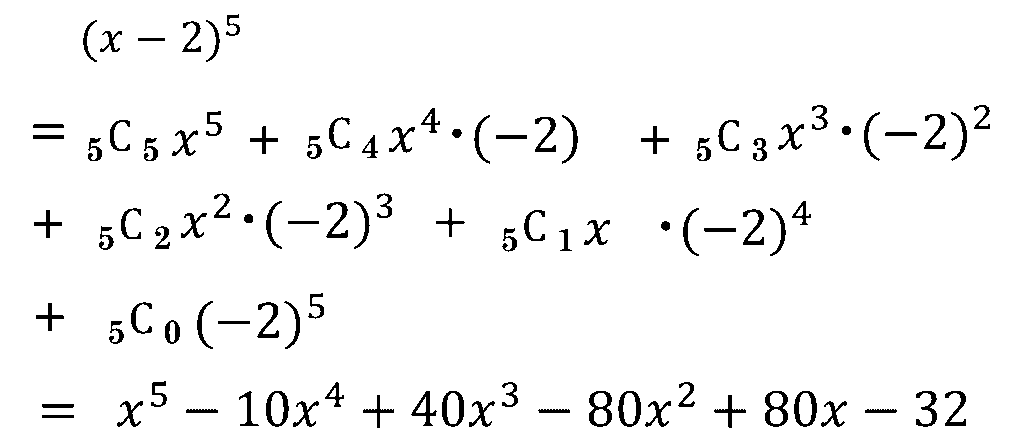
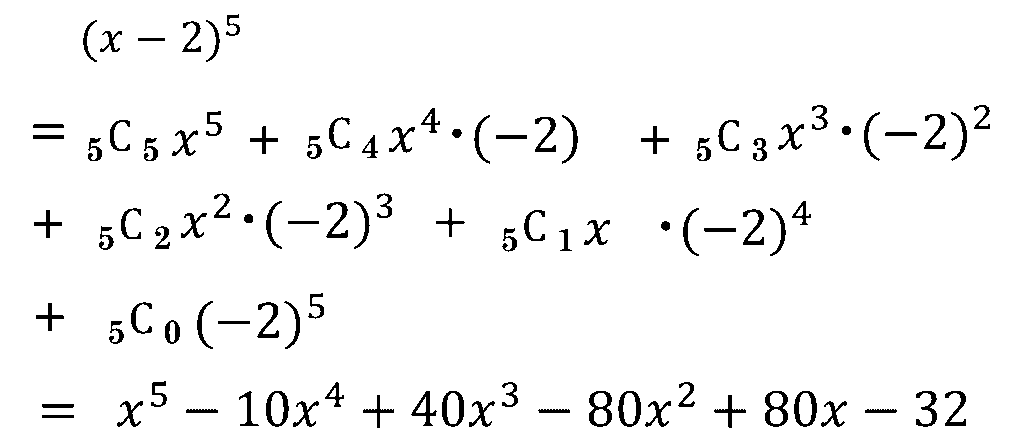
したがって、一般的に \((a+b)^n\) の展開は以下となります。
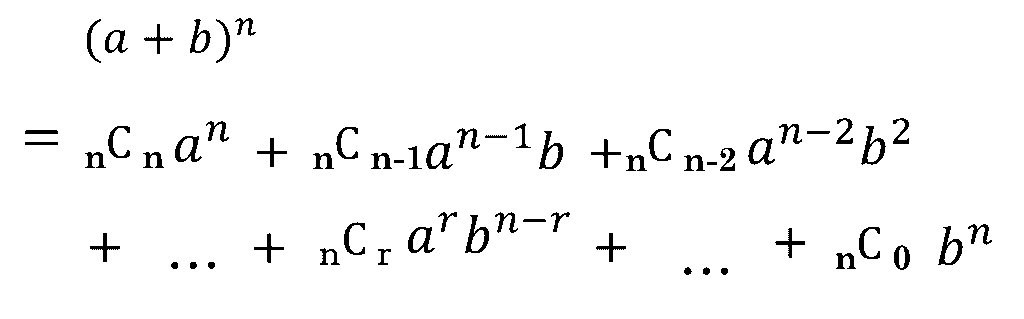
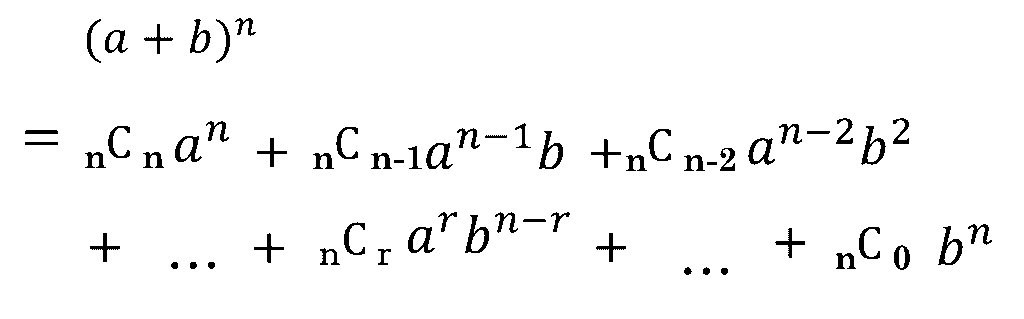



これが二項定理になります。二項定理を使えば、高次の展開ができたり、展開した後の項の係数を求めることができるところが利点です。
二項定理を利用した問題例
二項定理を利用した応用問題例としては例えば次のような問題があります。
問題 \((2x-1)^6\) の展開式における\(x^3\) の項の係数を求めよ。
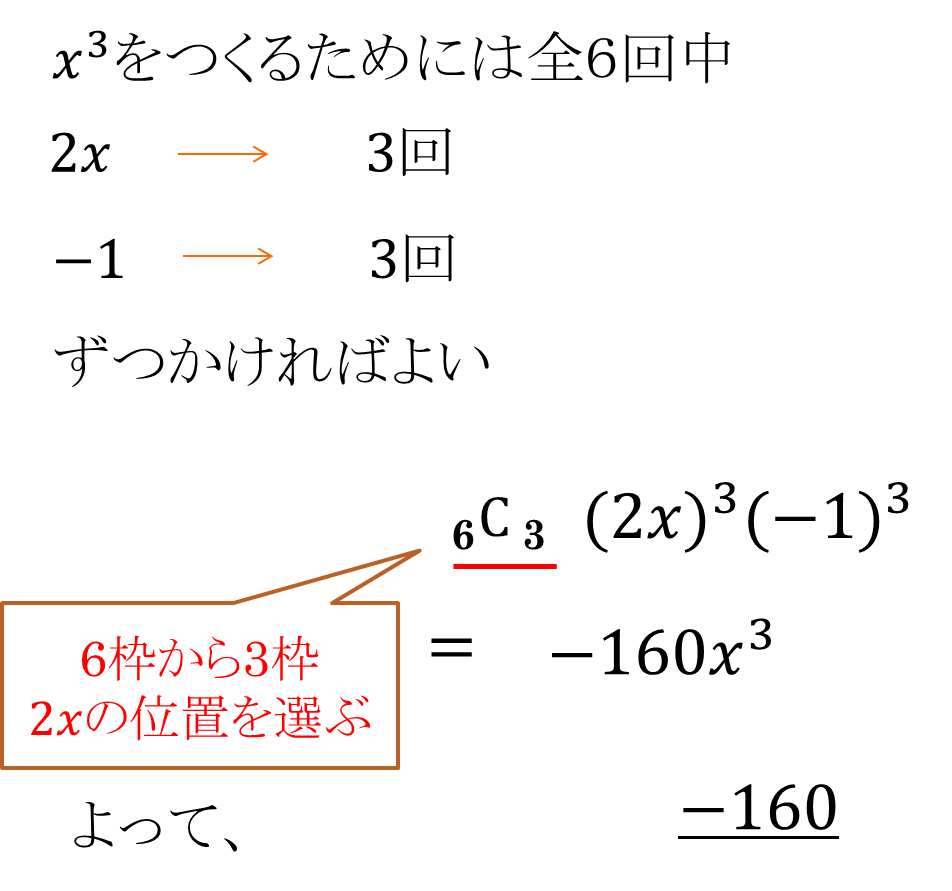




よくある問題集の解説では
一般項を\( {}_6 \mathrm{ C }_r(2x)^r(-1)^{6-r}\)とおき、これを満たす\(r\)を探していることが多いですが、難しければ上記の方法で全6回中\(2x\)と \(-1\) をそれぞれ何回かければ\((2x)^3(-1)^3\)の項ができるか考えるとわかりやすいかと思います。
二項定理はただの展開!難しく考える必要はなし!


今回は二項定理の基礎と応用問題例を紹介しました。
二項定理は一見難しいように感じますが、本記事でも紹介した通り、簡単にいえばただの高次の場合の展開にすぎません。
二項定理がよくわからない場合はまずは\((a+b)^3\)の展開の意味から考えるとわかりやすくなるかと思います。
数学の学習法を以下で紹介しています。
学習の仕方がわからない場合は是非チェックをしてみて下さい。





コメント