記事内に商品プロモーションを含む場合があります
\(ax^2 + bx + c = 0 (a \neq 0) \)
の形で表される方程式を2次方程式といいます。
この記事では、2次方程式の判別式について
「判別式とは何か」
「判別式が使える条件」
「判別式の計算を簡単にする方法(D/4)」
について解説しています。
2次方程式の判別式とは
判別式とは、「2次方程式の解の個数を判別できる式」のことをいいます。
方程式における実数の解を、単に実数解といいますが、例えば、以下のような問題があったとします。
例題 次の実数解の個数を求めよ。
① \(3x^2 + 7x + 1 = 0\)
② \(9x^2 – 6x + 1 = 0\)
③ \(x^2 – 3x + 3 = 0\)
これを、2次方程式の解の公式を利用して解くと以下のようになります。
2次方程式 \(ax^2 + bx + c = 0\) の解は、
\(x = \displaystyle\frac{-b \pm \sqrt{b^2 – 4ac}}{2a}\)

上記のように、実際に解を求めれば実数解の数を調べることはもちろんできます。
しかしながら、解の個数だけならば、解の公式におけるルートの中身、すなわち、\(b^2 – 4ac\) の符号によって、実数解の個数が決まることがわかります。
この値 \(b^2 – 4ac\) を判別式といい、\(\color{red}{D}\) を使って表します。

判別式が使える条件と使い方
判別式と実数解の個数について、次が成り立ちます。
2次方程式 \(ax^2 + bx + c = 0\) の判別式 \(D = b^2 – 4bc\) において
\(D > 0\) \(\iff\) 異なる2つの実数解をもつ
\(D = 0\) \(\iff\) ただ1つの実数解(重解)をもつ
\(D < 0\) \(\iff\) 実数解をもたない
ただし、上記が使える条件は以下になります。
① \(a \neq 0\) すなわち、 \(ax^2 + bx + c = 0\) が2次方程式であること。
② \(a, b, c\) は実数であること。(虚数のときは必ずしも成り立たない)
また、実際の使い方は以下になります。
例題 次の実数解の個数を求めよ。
① \(3x^2 + 7x + 1 = 0\)
② \(9x^2 – 6x + 1 = 0\)
③ \(x^2 – 3x + 3 = 0\)
① 判別式\(D = 7^2 – 4 \cdot 3 \cdot 1 = 37 > 0\)
よって、実数解の個数は 2個
② 判別式\(D = (-6)^2 – 4 \cdot 9 \cdot 1 = 0\)
よって、実数解の個数は 1個
③ 判別式\(D = (-3)^2 – 4 \cdot 1 \cdot 3 = -3 < 0\)
よって、実数解の個数は 0個
 シンスケ
シンスケこのように判別式の値を計算し、符号を調べることで、実数解の個数が簡単にわかります。
判別式の計算を簡単にする方法(D/4公式)
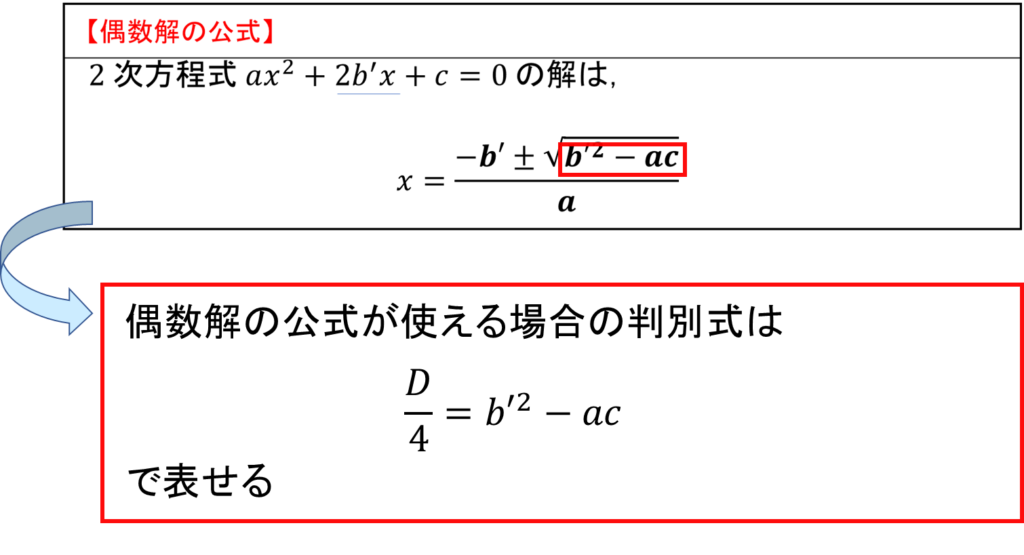
2次方程式\(ax^2 + 2b’ + c = 0\) (\(x\) の係数が偶数) の場合は、\(D\) の代わりに
\(\displaystyle\frac{D}{4} = b’^2 – ac\)
の符号を調べても解の個数を調べることができます。

例題 次の実数解の個数を求めよ。
\(x^2 – 6x + 3 = 0\)
判別式\(\displaystyle\frac{D}{4} = (-3)^2 – 1 \cdot 3 = 6 > 0\)
よって、実数解の個数は 2個



\(x\)の項の係数が偶数の場合は必ず約分でできる形になるため、 D/4 の公式を始めから利用した方が計算が速いです。
判別式を用いた問題例
判別式を利用した良く出る応用問題例としては以下のような問題があります。
例題 2次方程式 \(3x^2 – 5x + m = 0\) が異なる2つの実数解をもつように、定数\(m\) の値の範囲を求めよ。
異なる2つの実数解をもつとき、この2次方程式の判別式\(D > 0\) より
\(D = (-5)^2 – 4 \cdot 3 \cdot m > 0\)
よって、
\(m < \displaystyle\frac{25}{12}\)
上記のように、2次方程式において、「異なる2つの実数解をもつ」「重解をもつ」「実数解をもたない」のような文章が出てきたときは判別式を利用する問題であることが多いです。





コメント