 ラッシーくん
ラッシーくん三角比がまったくわからないのですが、これだけは知っておいた方がいい知識や公式などはありますか?
このような疑問や悩みに答えます。



中学高校の数学教諭として15年以上現場で教えています。
- 三角比とは?
- 三角比の定義
- 三角比の公式
- 三角比の拡張
- 三角比を使った面積公式
三角比は数学Ⅰの「図形と計量」の分野で扱われる内容ですが、sin , cos, tan といった新しく出てくるものや、公式も多いため苦手な方が多い印象です。
ここでは、三角比の内容について、これだけは知っておいて欲しい事項をまとめています。
三角比とは?
そもそも三角比とはその名の通り、三角形(直角三角形)の辺の比率のことです。
例えば、以下のような傾斜角20°の坂を500m進んだ場合に、水平方向と鉛直方向にはどれだけ進んだか知りたいとします。
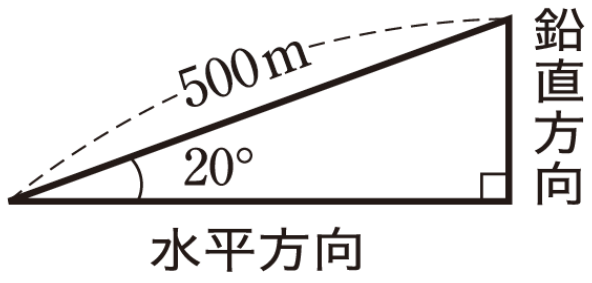

このような場合は、水平方向、鉛直方向を直接測量するのではなく、500mに傾斜角20°のときの倍率をかけることによって、実際の長さを測量することができます。
このときの長さの倍率のことを三角比といいます。
三角比の定義
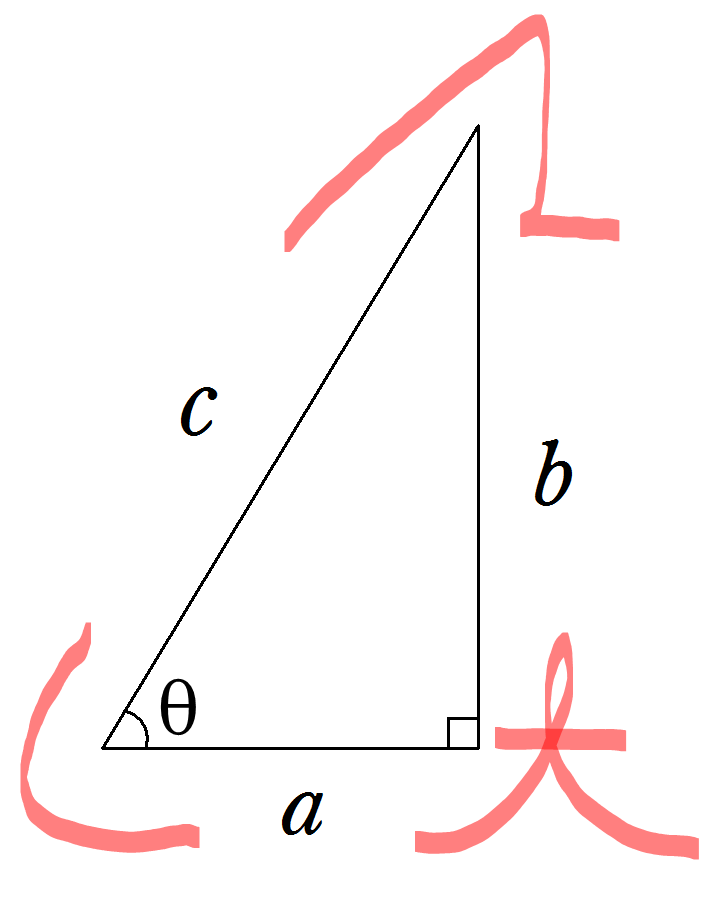
以下のような直角三角形において、長さをそれぞれ\(a\)(底辺)、\(b\)(対辺)、\(c\)(斜辺)とするとき、
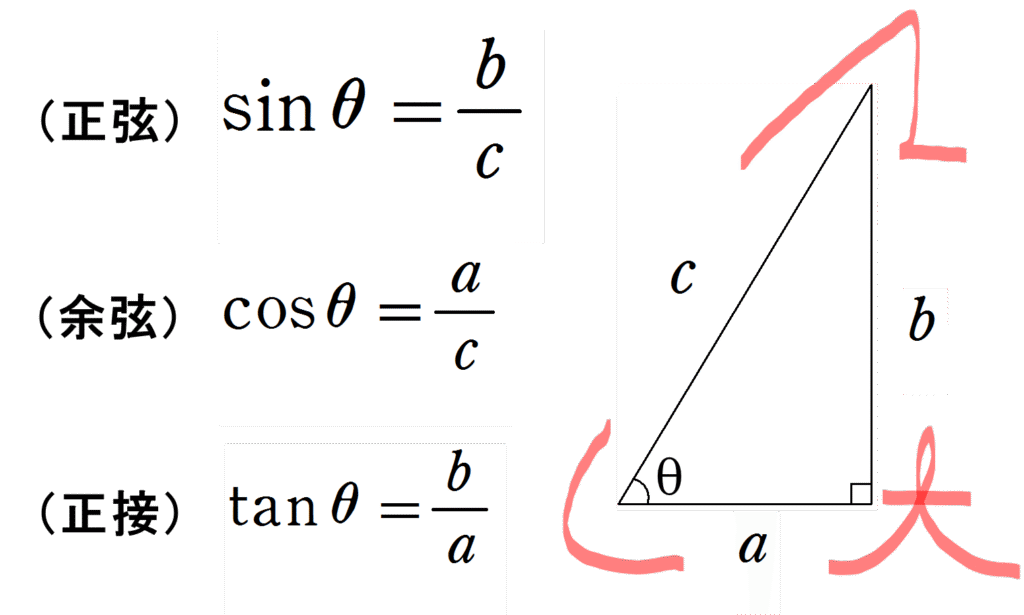

と定義します。
すなわち、


と変形できるため
- 正弦(サイン)sin\(\theta\)→ 斜辺 \(c\) に対する対辺 \(b\) の比率
- 余弦(コサイン)cos\(\theta\)→ 斜辺 \(c\) に対する底辺 \(a\) の比率
- 正接(タンジェント)tan\(\theta\)→ 底辺 \(a\) に対する対辺 \(b\) の比率
となります。
基本的な三角比の値
基本的な三角比の値は30°、45°、60°のときの三角比になります。
これらの値は、三角定規にもなっているように、辺の比率が広く知られており、以下のような三角比の値となります。
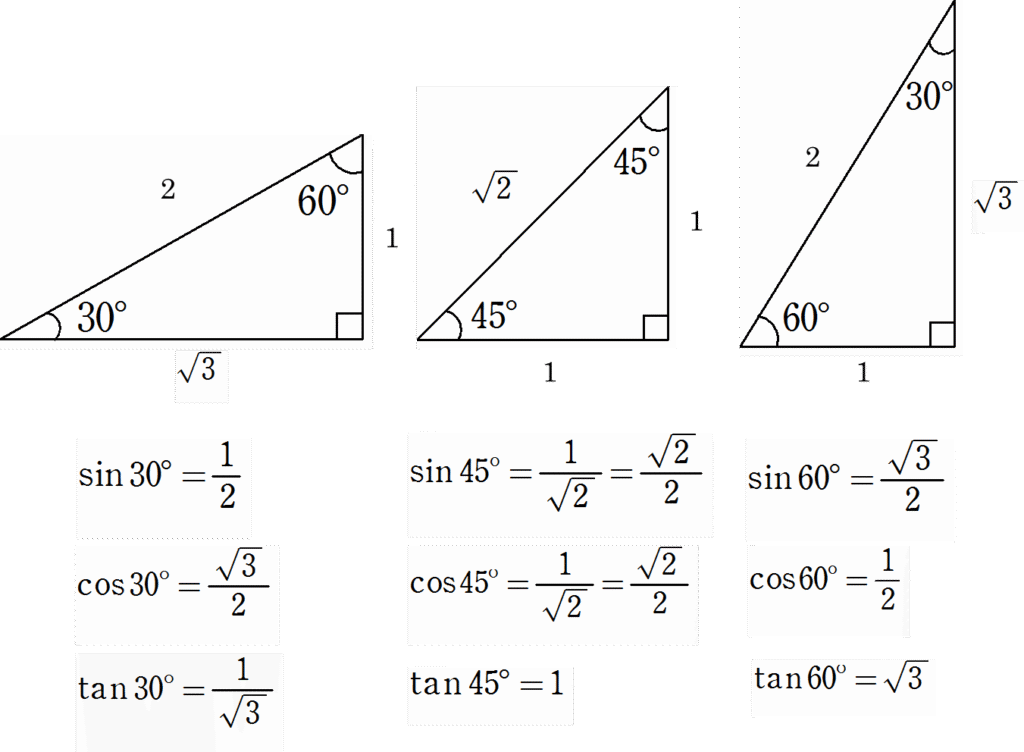
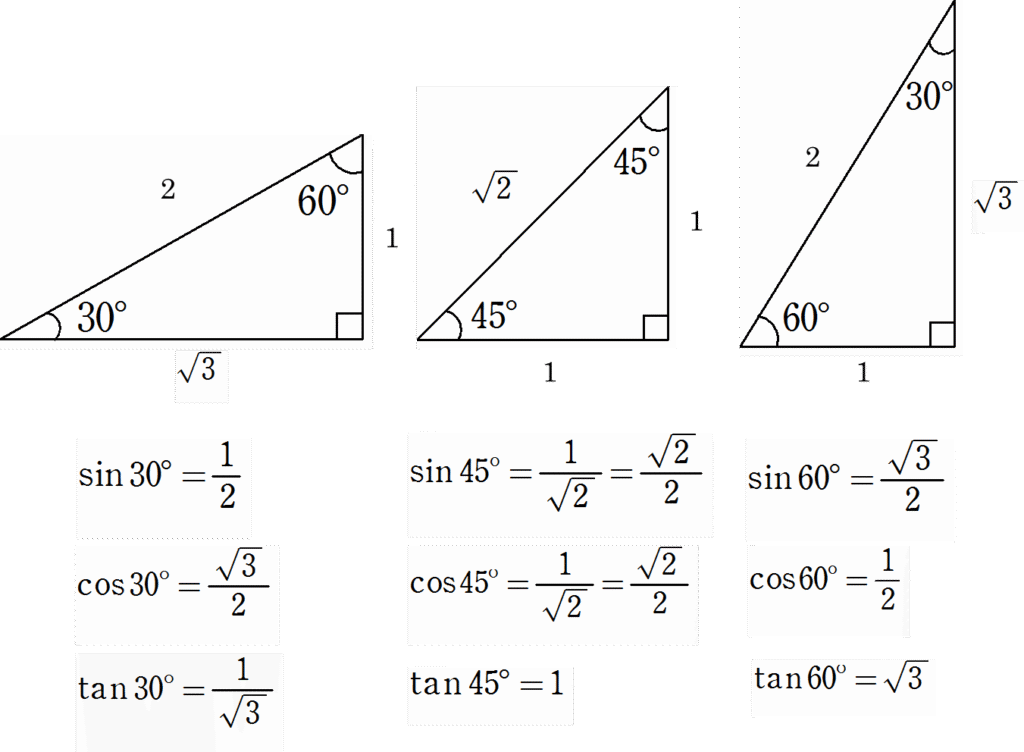



上記の値はとても重要ですので、しっかりと覚えておきましょう。
三角比の相互関係
三角比sin\(\theta\)、cos\(\theta\)、tan\(\theta\) の間には以下の3つの等式が常に成り立ちます。
- \(tan\theta = \frac{sin\theta}{cos\theta}\)
- \(sin^2 \theta +cos^2 \theta =1 \)
- \(1+tan^2 \theta =\frac{1}{cos^2 \theta}\)
証明
図において
\(b=c sin \theta\) …①
\(a=c cos \theta\) …②
このとき
\(tan \theta \)
\(=\frac{b}{a}\)
\(=\frac{c sin \theta}{c cos \theta}\)
\(=\frac{sin \theta}{cos \theta}\)
また、三平方の定理より、
\(c^2=b^2+a^2\)
\(c^2=(c sin \theta)^2+(c cos \theta)^2\)
\(c^2=c^2 sin^2 \theta+c^2 cos^2 \theta\)
\(c\neq0\)であるから 両辺\(c^2\)で割ると
\(sin^2 \theta +cos^2 \theta =1 \) …③
③の両辺を\(cos^2 \theta\) で割ると
\(\frac{sin^2 \theta}{cos^2 \theta} +1=\frac{1}{cos^2 \theta} \)
よって
\(1+tan^2 \theta =\frac{1}{cos^2 \theta}\)




この相互関係は三角比の分野だけでなく、数学Ⅱで扱う三角関数などでも多く扱います。
sin, cos, tan のどれか1つでもわかっている場合はこの相互関係を使って他の2つの値を求めることができますので非常に重要な公式です。
三角比の拡張
三角比は上記では直角三角形を用いて鋭角の三角比で考えていましたが、座標平面上に原点Oを中心とする半径1の半円をかき、この半円周上の点の座標を考えることで0°以上180°以下の角の三角比を定義することができます。
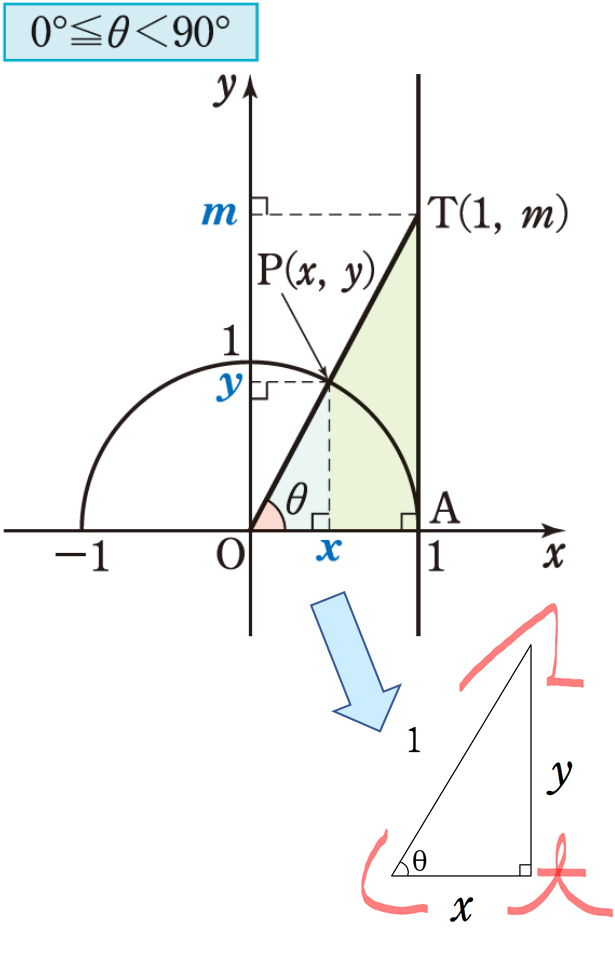

上記のように、半円周上に、点P(\(x , y\)) を
∠AOP=\(\theta\) (0°≦\(\theta\)≦180°)
となるようにすると、\(\theta\)の三角比は以下の式で表されます。


すなわち
- 正弦(サイン)sin\(\theta\)→ 単位円上の\(y\)座標の値
- 余弦(コサイン)cos\(\theta\)→ 単位円上の\(x\)座標の値
- 正接(タンジェント)tan\(\theta\)→ 単位円上の直線の傾き
このように考えることができるため、この値をみることで以下のように0°以上180°以下の角の三角比が決まります。
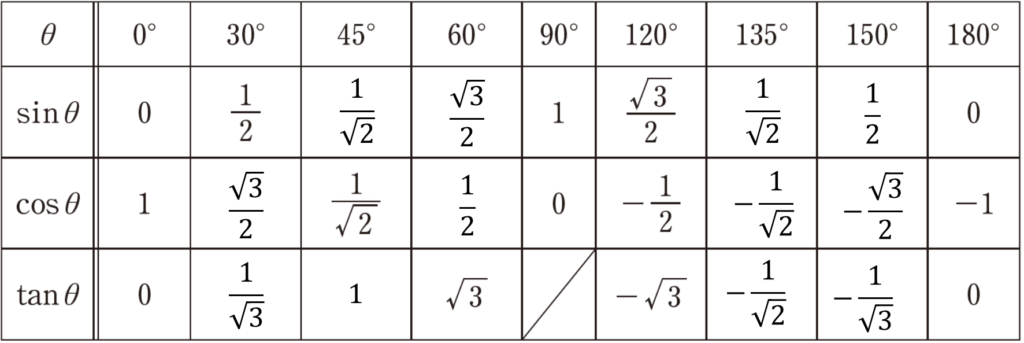

しかしながら、ここで注意点となりますが、上記の三角比の表は覚えないことをおすすめします。



理由としては、この先、三角比の値は上記以外の角度も出てくるからです。
実際は、三角比の値を求めるときは、以下の単位円(数学Ⅰの範囲では半円)を用いて、導き出しましょう。
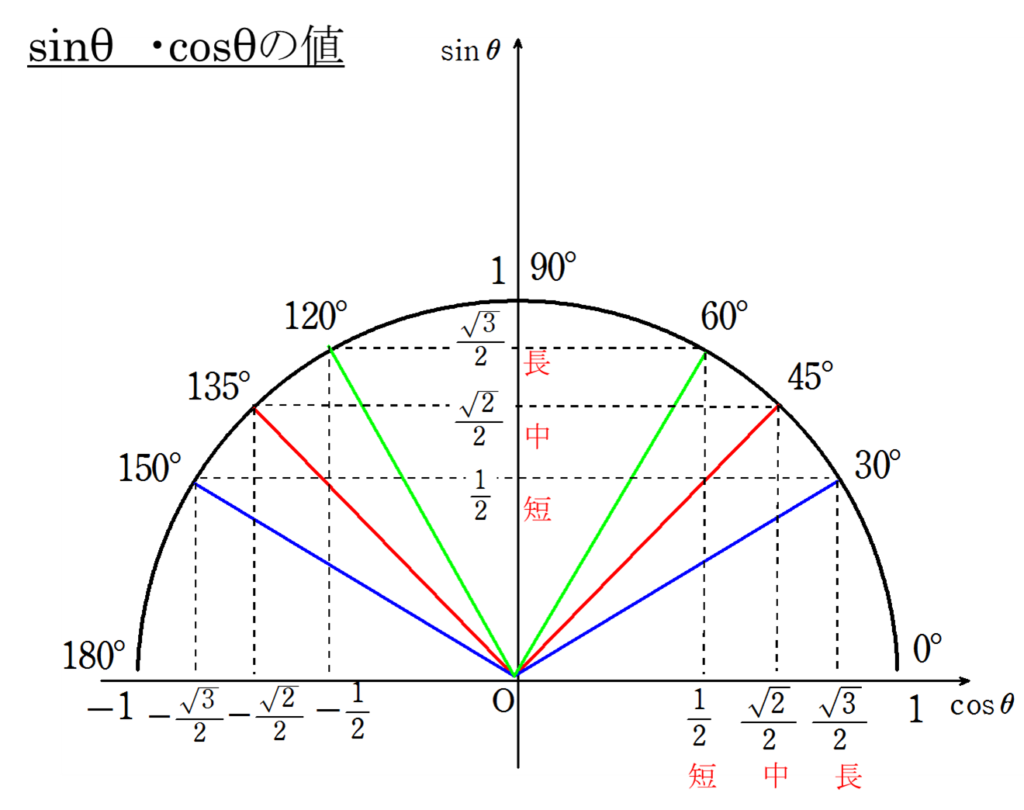

上図において、例えば、\(\theta=30°\)のときの値であれば、30°のときの\(x\)座標をみればcos の値 、\(y\)座標をみればsin の値を求めることができます。
すなわち、
cos30°=\(\frac{\sqrt{3}}{2}\
sin30°=\(\frac{1}{2}\)
となります。
また、tan の値も同様に単位円をかいて考えると今後の学習につながるようになります。
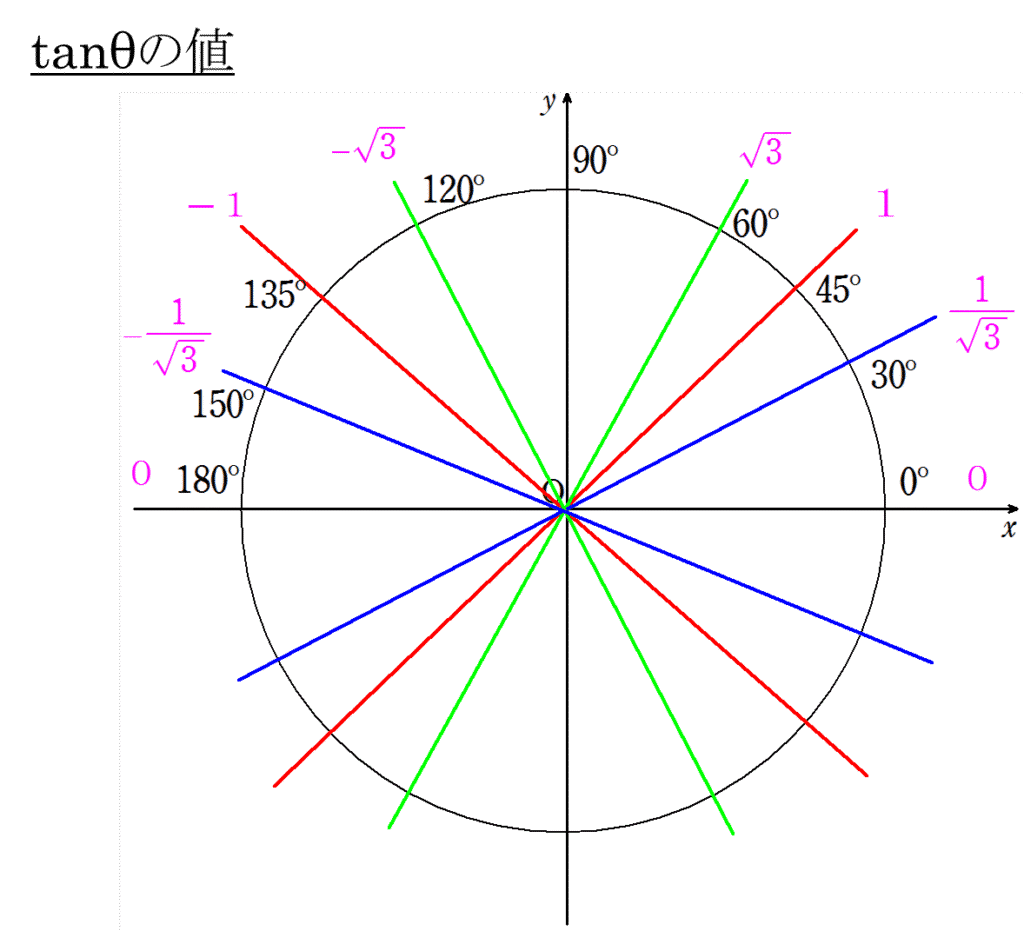

上図のように該当する角度のときの直線の傾きがtan の値となります。
例えば、
tan30°=\(\frac{1}{\sqrt{3}}\
となります。
正弦定理
三角形の1つの角の大きさと、それに向かい合う辺の長さの間には次の正弦定理が成り立ちます。
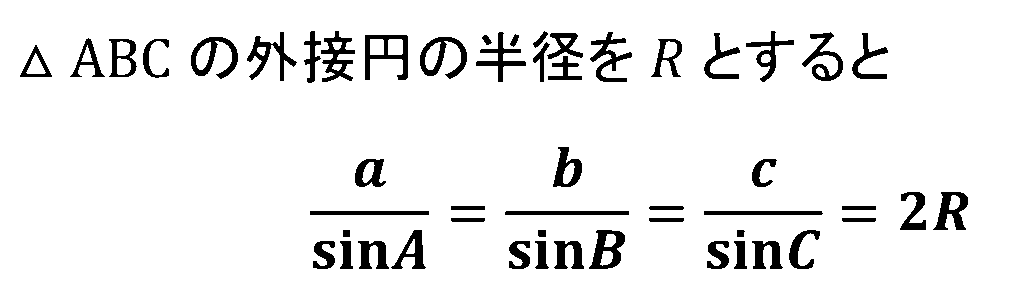
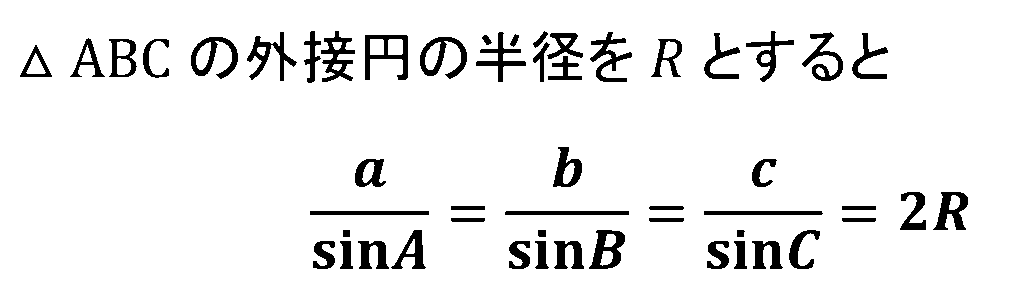
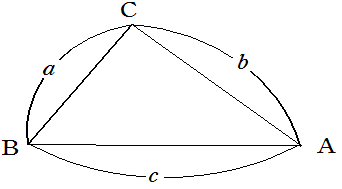

正弦定理は
主に三角形の1辺の長さと2つの角の大きさが与えられたときに、残りの2辺の長さを求めることができる定理となります。
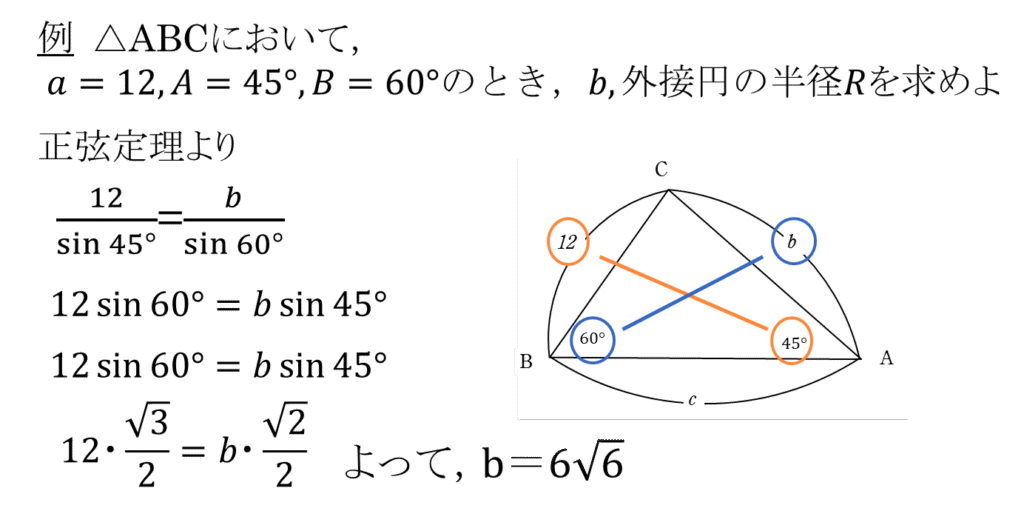

例えば上記のように、向かい合う辺と角の4つのうち3つまでわかっている場合は正弦定理を利用すると残りが求められます。
また、外接円の半径に関しても、正弦定理を使うことで求めることができます。



数学Ⅰで外接円の半径の長さを問われているときは、ほとんどの場合、正弦定理を利用する問題です。
上記のようにわかっている値を囲ってみるのがおすすめです。
余弦定理
三角形の3辺の長さの間には、次の余弦定理が成り立ちます。
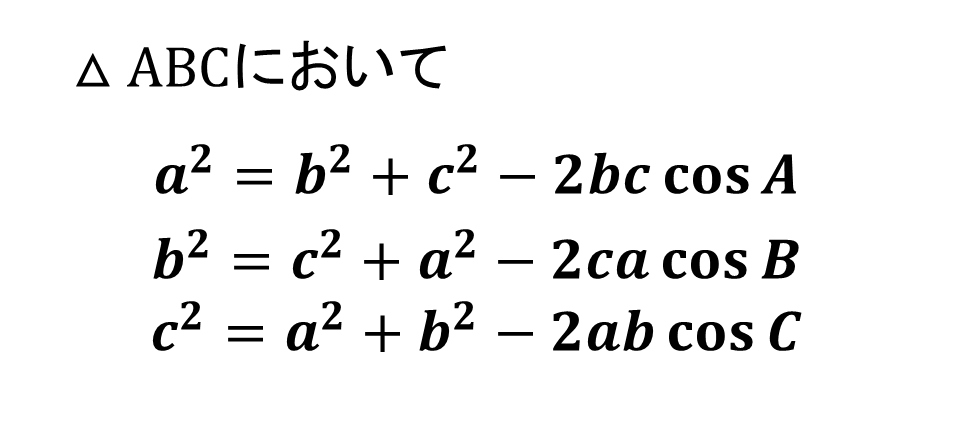
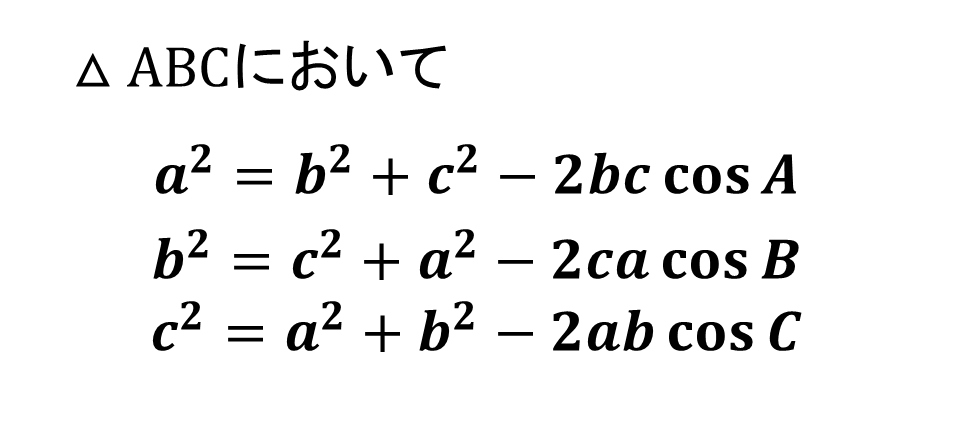


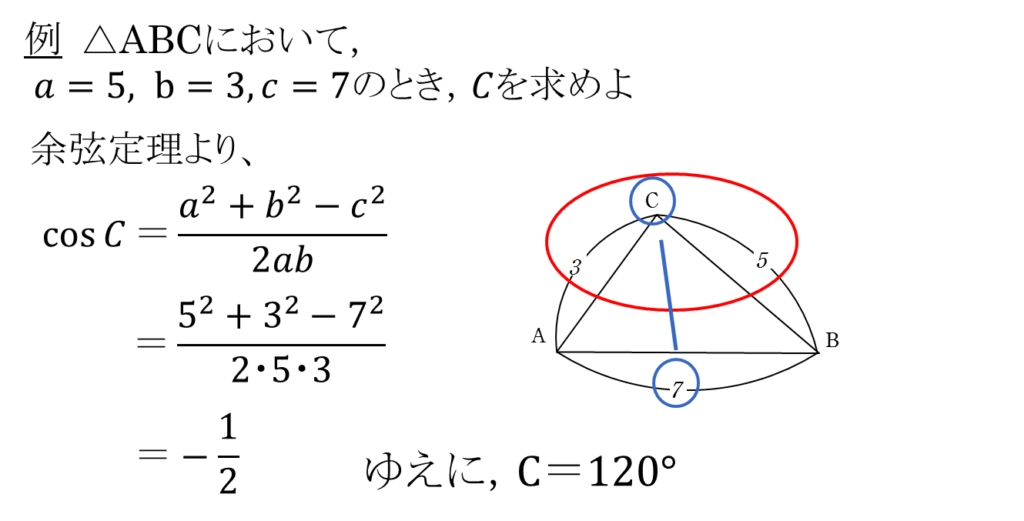
余弦定理は
主に三角形の2辺の長さと1つの角の大きさが与えられたときに、残りの辺の長さを求めることができる定理となります。
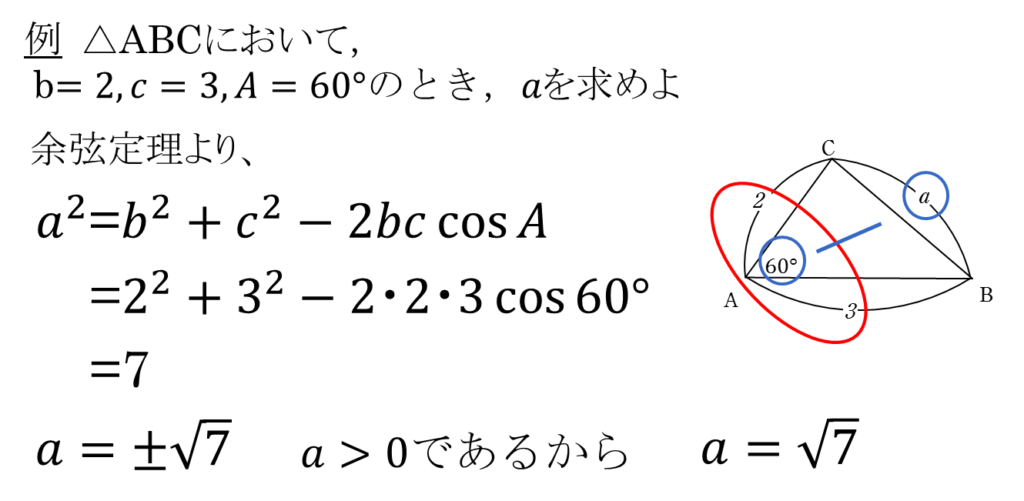

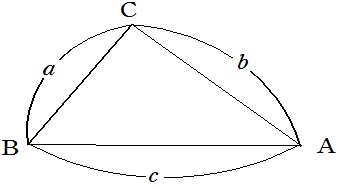
正弦定理と異なるのは、辺と角がわかっている箇所の違いです。
向かい合う辺と角どうしではなく、上の例のように2辺狭角とそれに向かう辺をみます。
また、余弦定理は以下の公式で使うこともあります。
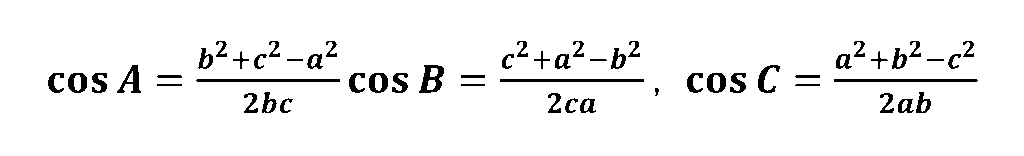
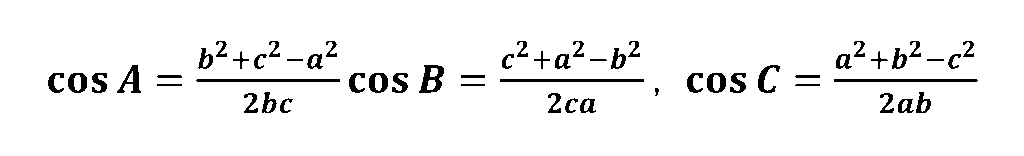


三角形の3辺の長さがわかっている場合は上記の公式の形で使った方が実際計算スピードは速くなりますが、「余弦定理①」でも解くこと自体は可能です。



必須とまではいきませんが、割りと問題で問われrことも多いため、できればこちらも使えるようになっておいた方がよいでしょう。
三角比を使った三角形の面積公式
三角形の面積は三角比を使うと以下で表すことができます。
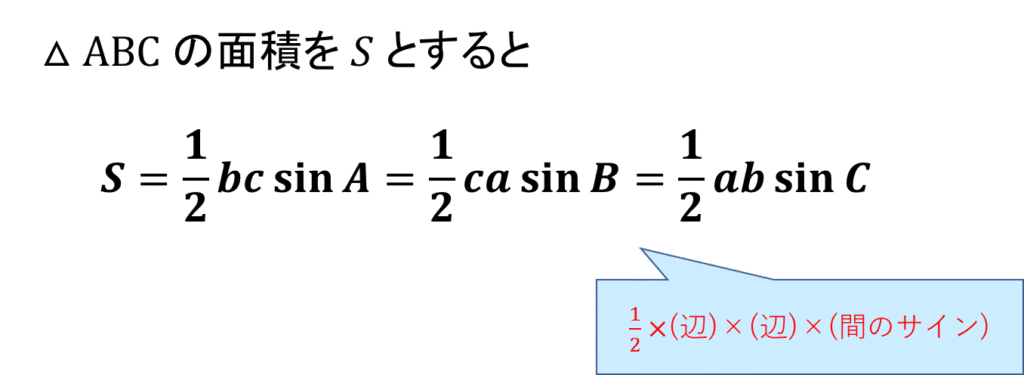
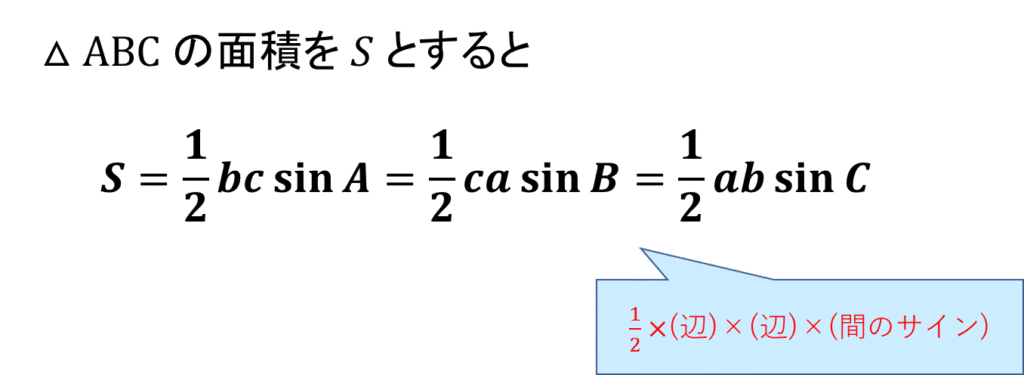


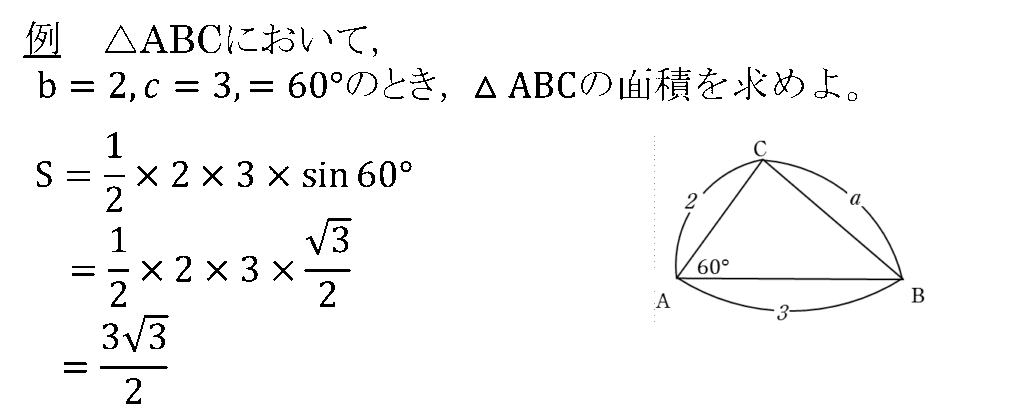




上記のCAsin\(60°\)の値は底辺ABに対する高さを表していますのでやっていることは、今での
\(\frac{1}{2}\)×(底辺)×(高さ)
の公式と同じです。
三角比はまずは基礎知識と公式を完璧にしよう!
今回は三角比の基礎知識と知っておきたい公式を紹介しましいた。
この記事で書かれた内容に関しては必ずおさえておかないと、応用問題に関しては解くことはできませんので忘れているものがあればこの機会に必ずおさえておきましょう。
特に、三角比の拡張の部分に関しては参考書や学校の教え方によっても
「表を覚えさせる方式」
「あくまでも直角三角形の辺の比で求める方式」
と様々な教え方をみかけますが、私の個人的な見解としては、今回紹介した、単位円で求められるようにした方が長い目でみると必ず得をすると感じます。
この機会に単位円の使い方をマスターしましょう。
数学の学習法を以下で紹介しています。
学習の仕方がわからない場合は是非チェックをしてみて下さい。




コメント