- 多項式の加法・減法・乗法
- 指数・累乗とは
- 多項式の展開公式
- 展開の工夫
多項式の加法・減法
ここでは、多項式の計算をしていきましょう。
多項式では、通常の数の計算と同様に次のような規則が成り立ちます。
\(A + B = B + A, AB = BA \)(交換法則)
\(A + B) + C = A + (B + C), (AB)C = A(BC)\) (結合法則)
\(A(B + C) = AB + AC , (A + B)C = AC + BC\)(分配法則)
 シンスケ
シンスケこれらは計算するときの基本的な規則となります。
多項式の和と差
まず、多項式の和と差の計算をしてみましょう。
例(多項式の和と差)
① \((3x^3 + 5x^2 – x + 3) + ( 5x^3 + 2x^2 + 3x – 2)\)
\(= (3 + 5)x^3 + (5 + 2)x^2 + (-1 + 3)x +(3 – 2)\)
\(= 8x^3 + 7x^2 + 2x + 1 \)
② \((3x^3 + 5x^2 – x + 3) – ( 5x^3 + 2x^2 + 3x – 2)\)
\(= 3x^3 + 5x^2 – x +3 – 5x^3 – 2x^2 – 3x + 2)\)
\(= (3 – 5)x^3 + (5-2)x^2 + (-1-3)x + (3 + 2)\)
\(= -2x^3 + 3x^2 – 4x + 5 \)
基本的には上記のように、
\(x^3\) の項は \(x^3\) の項どうし
\(x^2\) の項は \(x^2\) の項どうし
\(x\) の項は \(x\) の項どうし
定数項は定数項どうし
同類項をまとめていけばOKです。
ただし、②のように多項式どうしの差を考える場合は
\( – (5x^3 + 2x^2 + 3x – 2)\)
\(= – 5x^3 – 2x^2 – 3x + 2\)
のように分配法則によって、\(-\) がカッコ内の項に分配されますので、
カッコ内の各項の符号がすべて変わる点に注意しましょう。
多項式の乗法
指数とは
文字 \(a\) をいくつか掛けたものを \(a\) の累乗といい、\(n\)個掛けた場合は
\(a\)の\(n\)乗といい、\(a^n\)
のように表記します。
また、このときの\(n\)の部分を\(a^n\)の指数といいます。
例えば、
\(3 \times 3 \times 3 \times 3 \times 3 \)
は\(3\)を\(5\)回掛けていますので、
\(3^5\)
と表します。





指数は数学Ⅱでも扱う内容ですが、ここでもある程度はしっかりと理解しておきましょう。
指数法則
指数に関しては以下の指数法則が成り立ちます。
\(m , n \)は正の整数とする。
① \(a^m \times a^n = a^{m+n}\) ⇒ 掛け算は足し算
② \((a^m)^n = a^{mn}\) ⇒ 指数乗は掛け算
③ \((ab)^n =a^n b^n\) ⇒ 指数乗は分配できる
※\(a^0 =1 \)
例題
次の計算をせよ。
① \(a^3 \times a^2 \)
② \((a^4)^2 \)
③ \((ab)^3 \)
解答
① \(a^3 \times a^2 = a^{3+2}=a^5 \)
② \((a^4)^2 = a^{4 \times 2} =a^8\)
③ \((ab)^3 =a^3 b^3\)
ただ、暗記するのではなく、
① \(a^3 \times a^2 = aaa \times aa = a^{2+3}\)
⇒ 掛け算は指数乗の足し算
② \((a^4)^2 = aaaa \times aaaa = a^{4 \times 2}\)
⇒ 指数乗は掛け算
③ \((ab)^3 = ab \times ab \times ab\)
\(= aaa \times bbb = a^3b^3 \)
⇒ 指数乗は分配できる
このようになりますので、理屈もしっかりと抑えておくとよいでしょう。
多項式の乗法
続いて、多項式どうしの積を計算してみましょう。
例えば、多項式\((a+b)\)と多項式 \((c+d)\)の乗法に関しては、
\(A(B + C) = AB + AC , (A+B)C = AC + BC\)(分配法則)
によって以下が成り立ちます。
\((a+b) (c+d)\) …①
\(= a \cdot (c+d) + b \cdot (c+d) \) …②
\(= ac + ad + bc + bd \) …③
特に、①から②へは \(c+d\) をひとつの塊の文字だと思って、分配法則を利用しています。
②から③へも \(a\) と \(b\) をそれぞれ分配していますね。
しかしながら、ここで①から③への結果だけをみてみると
結局、①を計算した結果は、
多項式 \((a+b)\) と多項式 \((c+d)\) のすべての項どうしの掛け算をしていることになりますね。
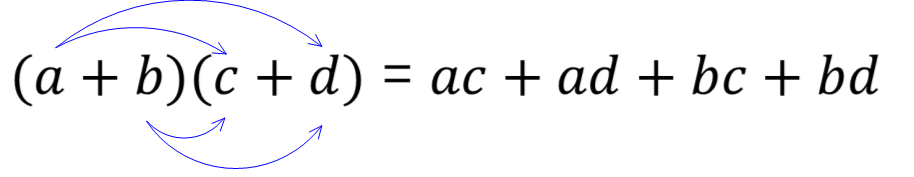
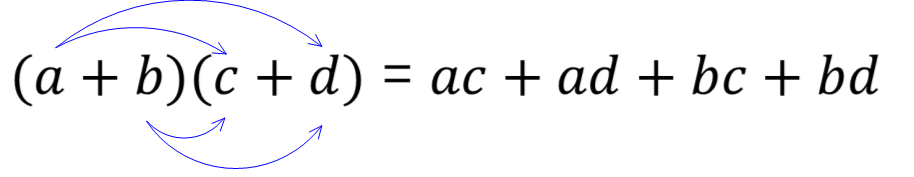
したがって、多項式の乗法に関しては、上記のように
多項式のすべての項どうしの掛け算をする
と覚えておくとよいでしょう。
例(多項式の乗法)
\((2x^2 + 3x + 1) (x+3)\)
\(=2x^2 \cdot x + 2x^2 \cdot 3 +3x \cdot x + 3x \cdot 3 \)
\(+ 1 \cdot x + 1 \cdot 3 \)
\(=2x^3 + 6x^2 + 3x^2 + 9x + x + 3\)
\(=2x^3 + 9x^2 + 10x + 3\)



\(6x^2\) と \(3x^2\) , \(9x\) と \(x\) は同類項になりますので必ず整理をしましょう。
このように、多項式の積を計算して、同類項を整理し、単項式の和の形に表すことを式を展開するといいます。
展開公式
基本の展開公式
多項式の展開に関しては、上記のように多項式のすべての項どうしの掛け算をする方法でも行うことができますが、特定の形をしている場合は以下の展開公式が成り立ちます。
①\((a+b)^2 = a^2 + 2ab + b^2\)
\((a-b)^2 = a^2 – 2ab + b^2 \)
②\((a+b) (a-b) = a^2 – b^2 \)
③\((x+a) (x+b) = x^2 + (a+b) x + ab \)
④\((ax+b)(cx+d) = acx^2 + (ad+bc) x + bd\)
例題
次の式を展開せよ。
① \((x+3y)^2 \)
② \((2a+b) (2a-b) \)
③ \((x+3) (x+2) \)
④ \((2x+3) (3x-5) \)
解答
① \((x+3y)^2 = x^2 + 2・x・(3y) + (3y)^2 = x^2 + 6xy + 9y^2\)
② \((2a+b) (2a-b) = (2a)^2 – b^2= 4a^2 – b^2 \)
③ \((x+3) (x+2) = x^2 + (3+2) x + 3 \cdot 2 = x^2 + 5 x + 6 \)
④ \((2x+3) (3x-5) \)
\(= 2 \cdot 3 x^2 + \{ 2 \cdot (-5) + 3 \cdot 3 \} x + 3 \cdot (-5) \)
\(= 6x^2 – x -15 \)



必ず上記を使わないと展開できないというわけではないですが、展開公式をしっかりと利用できるかどうかで、計算スピードが格段に変わります。
特に上記の①~③はしっかりと利用できるようになりましょう。
④に関しては、覚えられなければ分配法則を利用すればOKです。
\((a+b+c)^2\)の展開公式
\((a+b+c)^2\)の展開に関しては
\((a+b+c)^2\)
\(= (a+b+c) (a+b+c)\)
\(= a \cdot a + a \cdot b + a \cdot c + b \cdot a + b \cdot b\)
\(+ b \cdot c + c \cdot a + c \cdot b + c \cdot c \)
\(= a^2 + ab + ca + ab + b^2 + bc + ca + bc + c^2\)
\(= a^2 + b^2 + c^2 + 2ab + 2bc + 2ca\)
であることから以下の展開公式が成り立ちます。
\((a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca\)
例題
次の式を展開せよ。
\((x – 2y + z)^2 \)
解答
\((x – 2y + z)^2 \)
\(= x^2 + (-2y)^2 + z^2\)
\(+2 \cdot x \cdot (-2y)+2 \cdot (-2y) \cdot z +2 \cdot z \cdot x\)
\(= x^2 + 4y^2 + z^2 – 4xy – 4yz + 2zx\)
カッコ内の項に着目して
(それぞれの項の2乗の足し算)+(それぞれの項の2倍の組み合わせの足し算)
と覚えると簡単です。



これは例えば、数検準2級の1次試験でもよく出題されます。
分配法則でもできますが、公式として覚えてしまう方が便利です。
展開(式の計算)の工夫
複雑な展開を行う際は以下のような手法をとることで、計算しやすくなることがあります。
特定の部分を1つの文字と考えて展開公式を利用する
特定の部分を1つの文字と考えて展開公式を利用することで、通常の分配法則よりも展開しやすくなることがあります。
例えば、\((a+b+c)^2\) の展開をもう一度考えてみましょう。
これは, \(a+b\)を1つの文字として考えることで以下のように2乗の展開公式を使って計算することができます。
例①(特定の部分を1つの文字と考えて展開公式)
\((a + b + c)^2\)
\(= \{(a + b)^2 + c\}^2\)
\(= (a + b)^2 + 2(a+b)c + c^2\)
( \(a + b\) を1つの文字と考えて展開)
\(= a^2 + 2ab + b^2 +2ac + 2bc + c^2\)
(\((a + b)^2 = a^2 + 2ab + b^2 \) を利用)
\(= a^2 + b^2 + c^2 + 2ab + 2bc + 2c\)
このように、ある特定の部分(今回の場合は \(a+b\) \)を1つの文字と考えて、なるべく展開公式を利用すると複雑な展開にも対応できることがあります。
例②(特定の部分を1つの文字と考えて展開公式)
\((x + 2)^2(x – 2)^2\)
\(= \{(x + 2)(x – 2)\}^2\)
( \(A^2B^2 = (AB)^2\) を利用)
\(= (x^2 – 2^2)^2\)
(\((a + b)(a – b) = a^2 – b^2\) を利用)
\(= (x^2 – 4)^2\)
\(= (x^2)^2 – 2 \cdot x^2 \cdot 4 + 4^2\)
(\((a – b)^2 = a^2 – 2ab + b^2 \) を利用)
\(= x^4 – 8x^2 + 16\)
これもポイントは\((x + 2)\)と\((x – 2)\)を1つの文字して考え、\(A^2B^2 = (AB)^2\) を利用することで、基本の展開公式が利用できる形にもっていっています。
和の順序を入れ替える
和の順序を入れ替えることで、上記のような共通部分をつくることができるときもあります。
例(和の順序を入れ替える)
\((a^2 + ab + b^2) (a^2 – ab + b^2) \)
\(= \{(a^2 + b^2) + ab\} \{(a^2 + b^2) – ab \} \)
\(= (a^2 + b^2)^2 – (ab)^2\)
\(= a^4 + 2a^2b^2 + b^4 – a^2b^2\)
(\((A + B)^2 = A^2 + 2AB + B^2 \) を利用)
\(= a^4 + a^2b^2 + b^4\)



このように、1つの文字の塊をつくったり、順序を入れ替えることで工夫できる例はたくさんあります。
展開公式が利用できる形を積極的につくっていきましょう。




コメント