【数と式】１ー１．単項式・多項式とは～係数・次数・同類項・降べきの順に整理～

単項式と多項式とは～係数・次数～

単項式の係数と次数

数や文字を掛け合わせてできる式のことを単項式といいます。

単項式の例：　\(3a^2 , -5x^2y\)

また、単項式において，数の部分を係数，かけ合わせた文字の個数を次数　といいます。

例（単項式の係数と次数）

①　\(5x^2\) ⇒　係数：\(5\), 次数：\(2\)
②　\(-3xyz\) 　⇒　係数：\(-3\), 次数：\(2\)
③　\(a^2bc\) 　⇒　係数：\(1\), 次数：\(4\)

上記の通り、係数は基本的に文字の前の数字を読めばOKです。ただし、③のように数字がない場合は係数が\(1\)となります。（係数が \(1\) の場合は省略する）

次数に関しては文字が何回かけられているか考えましょう。

例えば、③は

\(a^2bc\)　⇒　\(a \times a \times b \times c \)　

のように文字が\(4\)回かけられていますので次数は\(4\)となります。

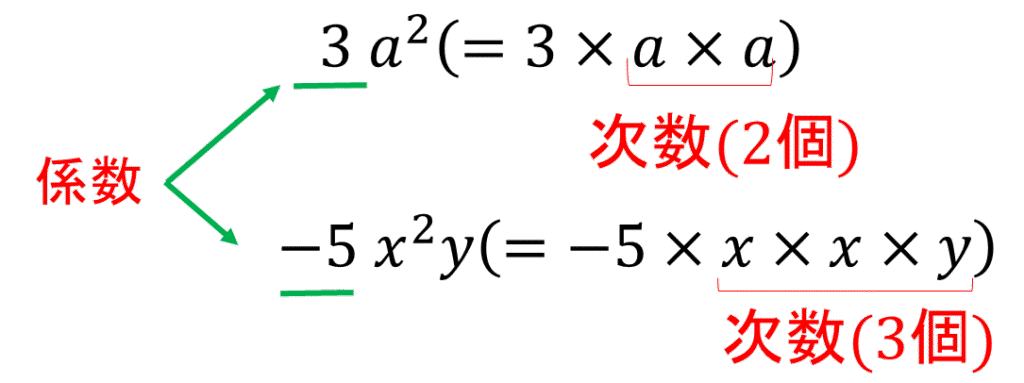
２種類以上の文字を含む単項式の係数と次数

２種類以上の文字を含む場合は、特定の文字に着目して（特定の文字以外数字扱いとして）考えることがあります。

例（２種類以上の文字を含む単項式の係数と次数）

単項式 \(2ax^2y^3\) の係数と次数は
①　\(x\)に着目する（\(x\)だけ文字, \(y\), \(a\)は数字と考える）と
⇒　係数：\(2ay^3\) , 次数：\(2\)
②　\(y\)に着目する（\(y\)だけ文字, \(x\), \(a\)は数字と考える）と
⇒　係数：\(2ax^2\) , 次数：\(3\)
③　\(a\)に着目する（\(a\)だけ文字, \(x\), \(y\)は数字と考える）と
⇒　係数：\(2x^2y^3\) , 次数：\(1\)

上記のように，どの文字に着目したかによっても係数と次数は変わってきます。

多項式

多項式とはいくつかの単項式の和の形で表される式のことをいいます。

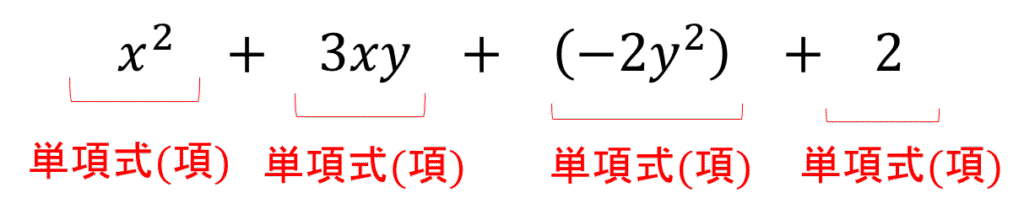
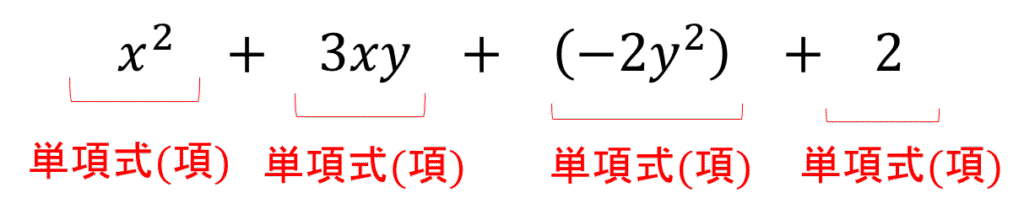
多項式のことを整式ともいいます。

例（多項式）

①\(2x^2 + 3x -1\)
② \(5x – 1\)

各単項式のことを多項式の項といいます。

例えば上記の「①\(2x^2 + 3x -1\)」の場合、

項は

\(2x^2, 3x, -1 \)

となります。

単項式・多項式とは～同類項の整理・降べきの順～

同類項の整理

多項式の項の中で文字の部分が全く同じ項のことを同類項といいます。

例えば、

\(2x^2 – x + 3x^2 -3 \)

において、

\(2x^2\)と\(3x^2\)の項は文字の部分がどちらも\(x^2\)で全く同じなので同類項です。

同類項どうしは１つにまとめて整理することができます。

例（同類項の整理）

①　\(3x^2 – x + 2x^2 +2 -5x+3\)
\( = (3+2)x^2 +(-1-5)x+(2+3)\)
\(=5x^2-6x+5\)

②　\(x^2 – 2x^2y^2 + 3x^2y^2 -5x^2+3y^2\)
\(=(1-5)x^2 +(-2+3)x^2y^2 +3y^2\)
\(=-4x^2+x^2y^2+3y^2\)

多項式の次数に関しては、上記のように同類項を整理したときに、最も次数の高い項の次数をこの多項式の次数と定義し、次数が\(n\)の多項式を\(n\)次式といいます。

例（多項式の次数）

①　\(=5x^2-6x+5\)
⇒　最も次数の高い次数の項\(5x^2\)の次数は\(2\)次より、この多項式は\(2\)次式

②　\(=-4x^2+x^2y^2+3y^2\)
⇒　最も次数の高い次数の項\(x^2y^2\)の次数は\(4\)次より、この多項式は\(4\)次式

定数項

多項式において、定数のみの（特定の文字を含まない）項のことを定数項といいます。

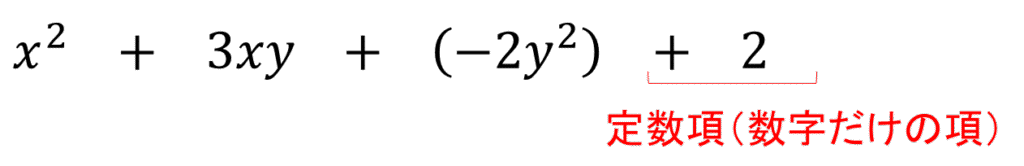
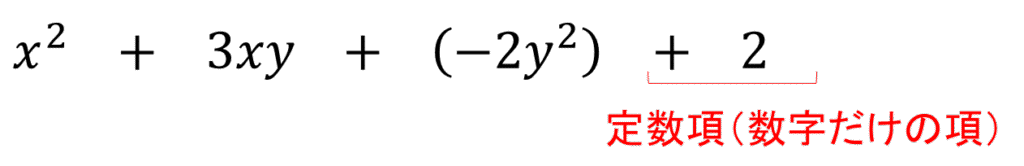
例（定数項）

①　\(2x^2+5x+2\)
⇒　\(2\)次式で定数項は\(2\)

②　\(ax^3y^2 + bx + c\)
⇒　\(x\)に着目する(\(a, b, c, y\)は数字扱いとする)と，\(3\)次式で定数項は\(c\)
⇒　\(y\)に着目する(\(a, b, c, x\)は数字扱いとする)と，\(2\)次式で定数項は\(bx+c\)
⇒　\(x\)と\(y\)に着目する(\(a, b, c\)は数字扱いとする)と，\(5\)次式で定数項は\(c\)

定数項は基本的には①のように数字の部分のみの項のことをいいますが、②のように着目する文字によっては文字も数字扱いとして考えるところに注意しましょう。

降べきの順・昇べきの順に整理する

項の次数が高い方から順に並べることを降べきの順に整理するといい，

項の次数が低い方から順に並べることを昇べきの順に整理するといいます。

例（降べきの順・昇べきの順に整理

多項式\(2x-x^2+7+x^3+2x^4\)
降べきの順（次数の高い順）に整理（同類項をまとめる）　⇒　\(2x^4+x^3-x^2+2x+7\)　
昇べきの順（次数の低い順）に整理（同類項をまとめる）　⇒　\(7+2x-x^2+x^3+2x^4\)

特定の文字について降べきの順に整理する

２種類以上の文字が入った場合でもある特定の文字に着目することで降べきの順に整理することができます。

例（特定の文字について降べきの順に整理）

多項式\(2x^2-3xy+3y^2-2x+7y+5\)
\(x\)について降べきの順に整理　⇒ \(2x^2+(-3y-2)x+(3y^2+7y+5)\)
\(y\)について降べきの順に整理　⇒ \(3y^2+(-3x+7)y+(2x^2-2x+5)\)

>> 「1-2. 多項式の加法・減法・乗法」へ進む