- 実数とは~整数・自然数・有理数・無理数・実数の違い~
- 絶対値とは
実数とは何か
実数とは簡単にいうと
「数直線やグラフ上にかける数」
のことをいいます。
 シンスケ
シンスケ「実際にある数」なので実数です。
ちなみに、実数ではない数のことを「虚数」といいますが、これは数学Ⅱの範囲で扱います。
例えば、
整数、小数、分数、自然数など中学校までで習う数はすべて数直線上に表せるので実数です。
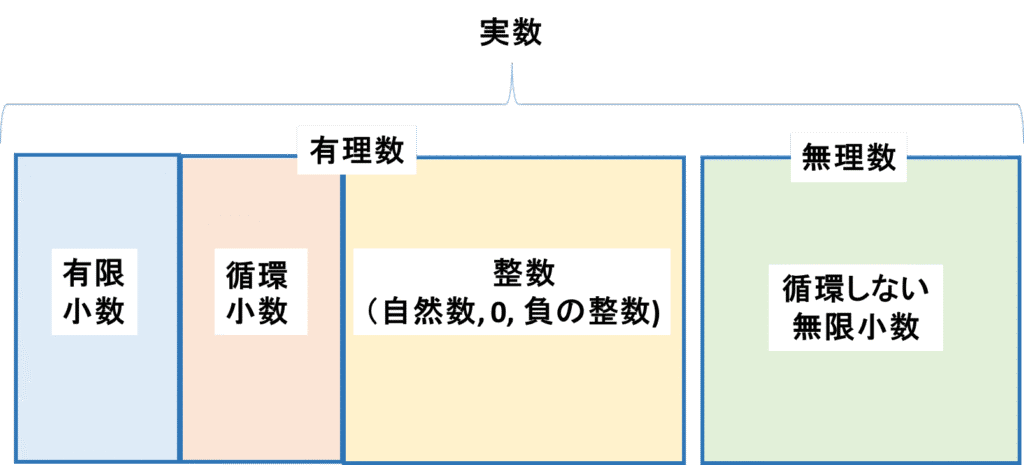
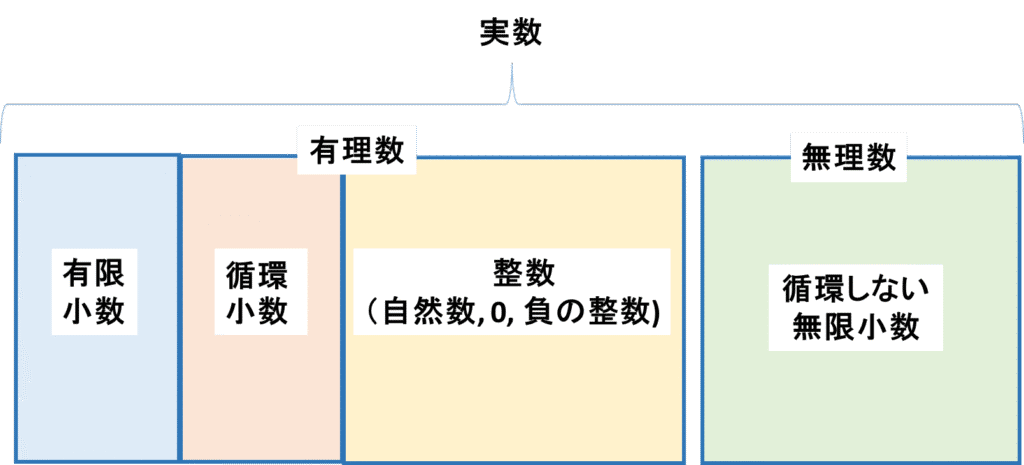
実数は大きく「有理数」と「無理数」の2つに分かれます。
全体的なイメージ

実数とは~有理数について解説~
実数の中でも、まずは有理数についてみていきましょう。
有理数とは
分数で表される数
のことをいいます。
しっかりとした定義は次のようになります。
整数\(m\) と\(0\) でない整数\(n\) を用いて分数 \(\frac{m}{n}\) の形に表される数のことを有理数という。



整数を使った分数の形で表される数はすべて有理数となります。
実際に、有理数の例をみていきましょう。
有理数の例①:整数
\(0\) および \(0\) に次々に \(1\) を足したり引いたりしてできる数、すなわち
\(\cdots \cdots -3, -2, -1, 0, 1, 2, 3, \cdots \cdots\)
のことを整数 といいます。



上記のようにキリの良い数字がすべて整数です。
マイナスの数や \(0\) も含まれる点に注意しましょう。
整数に関しては、例えば
\(5 = \displaystyle\frac{5}{1}\)
となるため、分数 \(\frac{m}{n}\) の形で表せます。
したがって、整数は有理数です。
有理数の例②:自然数
整数の中で正のもの、すなわち
\( 1, 2, 3, \cdots \cdots\)
のことを自然数といいます。



自然数は簡単にいえば、正の整数のことです。
したがって、自然数はそもそも整数に含まれますので有理数です。
有理数の例③:有限小数
\(0.1, 8.25\)
のように終わりがある小数のことを有限小数といいます。
例えば、
\(0.1 = \displaystyle\frac{1}{10}\)
\(8.25 = \displaystyle\frac{825}{100} = \displaystyle\frac{33}{4}\)
と分数で表せるので有理数です。



\(\displaystyle\frac{33}{4}\) のようにこれ以上約分できない分数を既約分数といいます。
有理数の例④:循環小数
\(1.33333 \cdots \cdots , 1.0185185 \cdots \cdots\)
のようにある特定の数字の配列が繰り返される小数を循環小数といいます。
例えば、
\(\displaystyle\frac{4}{3} = 1.33333 \cdots \cdots\)
\(\displaystyle\frac{55}{54} = 1.0185185 \cdots \cdots\)
となりますので、
\(1.33333 \cdots \cdots \) や \(1.0185185 \cdots \cdots\)
のような循環小数は有理数となります。
ここで,
循環小数は上記のままだと長くなってしまいますので,通常は
\(1.33333 \cdots \cdots → 1.\dot{3} \)
\(1.0185185 \cdots \cdots → 1.0\dot{1} 8 \dot{5}\)
のように表します。



繰り返す部分の最初と最後の数字に点を打てばOKです。
実数とは~無理数について解説~
実数の中で、有理数でない数、すなわち
循環しない無限小数で表される数のことを無理数といいます。
例えば
\(\sqrt{2} = 1.414213\cdots\cdots\)
\(\sqrt{3} = 1.7320508\cdots\cdots\)
\(\pi = 3.1415926535\cdots\cdots\)
となり、これらは無限小数かつ特定の数字の配列が繰り返されるわけでもありません。
したがって、これらは無理数となります。
実数とは~まとめと例題~
ここまでの内容のまとめと例題は以下のようになります。

例題
次の数の中から①自然数, ②整数, ③有理数, ④無理数 をそれぞれ選べ。
\(-2, 0, \displaystyle\frac{35}{5}, \displaystyle\frac{5}{2}, -\displaystyle\frac{7}{8},\)
\( -\sqrt{2}, \sqrt{16}, \displaystyle\frac{3}{\sqrt{3}}, (\sqrt{7})^2, \pi\)
解答
与えられた数において
\(-2\) (有理数かつ整数)
\(0\) (有理数かつ整数)
\(\displaystyle\frac{35}{5}=7\)(有理数かつ整数かつ自然数)
\(\displaystyle\frac{5}{2}=2.5\)(有限小数より、有理数)
\(-\displaystyle\frac{7}{8}=-0.875\)(有限小数より、有理数)
\(-\sqrt{2}=-1.4142 \cdots \)(循環しない無限小数より、無理数)
\(\sqrt{16}=4\)(有理数かつ整数かつ自然数)
\(\displaystyle\frac{3}{\sqrt{3}}=\sqrt{3}=1.732\cdots\)(循環しない無限小数より、無理数)
\((\sqrt{7})^2=7\) (有理数かつ整数かつ自然数)
\(\pi =3.141592 \cdots\)(循環しない無限小数より、無理数)
したがって、
① 自然数は \(\displaystyle\frac{35}{5}, \sqrt{16},(\sqrt{7})^2\)
② 整数は \(-2, 0, \displaystyle\frac{35}{5}, \sqrt{16}, (\sqrt{7})^2\)
③ 有理数は \(-2, 0, \displaystyle\frac{35}{5}, \displaystyle\frac{5}{2}, -\displaystyle\frac{7}{8}, \sqrt{16}, (\sqrt{7})^2\)
④ 無理数は \(-\sqrt{2}, \displaystyle\frac{3}{\sqrt{3}}, \pi \)
実数とは~絶対値について解説~
実数どうしの距離について考えていきましょう。
数直線上における原点\(O(0)\) と点\(P(a)\) との距離を,実数\(a\) の絶対値といい、
実数\(a\) の絶対値であれば \(|a|\)
と表します。
例えば、
① \(|3| = 3\)
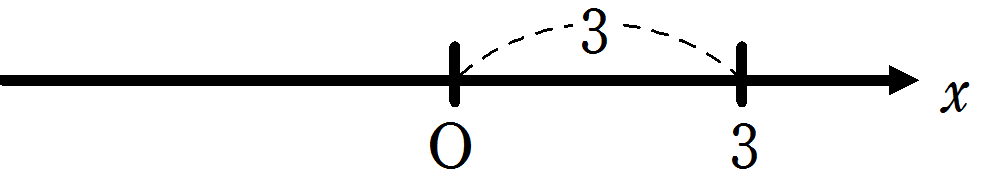
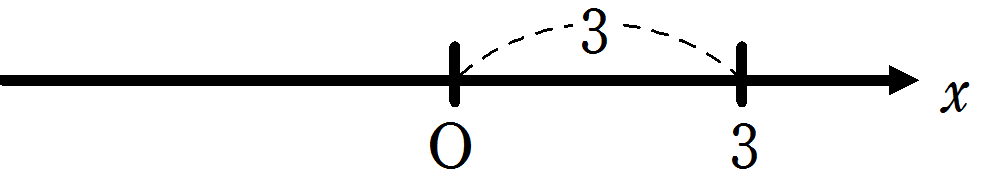



原点 O から \(3\) までの距離は\(3\)です。
したがって、絶対値の中が正のときは、絶対値はそのまま外せばOKです。
② \(|-2| = -(-2) = 2\)
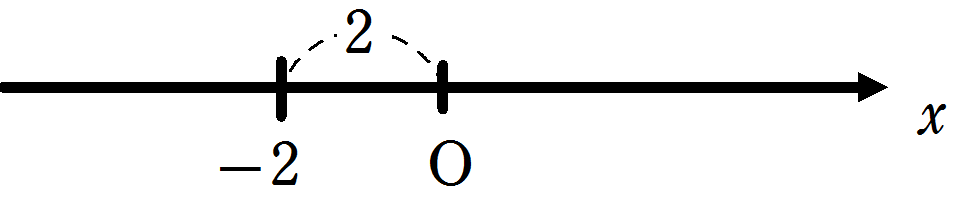



原点 O から \(-2\) までの距離は\(2\)です。
したがって、絶対値の中が負のときは、絶対値はマイナスをつけて外し、値は正になります。
絶対値の外し方
絶対値の中が正 → そのまま外す
絶対値の中が負 → −をつけて外す
\( \begin{eqnarray} |x| = \begin{cases} x & (x \geq 0 のとき) \\ -x&(x \lt 0のとき) \end{cases}\end{eqnarray}\)
例題
次の値を求めよ。
① \(|-3|\)
② \(|3.7|\)
③ \(|\pi -4|\)
解答
① \(|-3| =-(-3)=3\)
② \(|3.7|=3.7\)
③ \(|\pi-4|=-(\pi-4)=-\pi+4\)





コメント