- 平方根とは
- 根号を含む式の性質と計算公式
- 分母の有理化
根号を含む式の計算~平方根・有理化~
平方根とは
例えば
\(2\) や \(-2\) は2乗すると\(4\)になるかと思いますが,逆に2乗して \(4\) になる数のことを \(4\) の平方(2乗)根といいます。
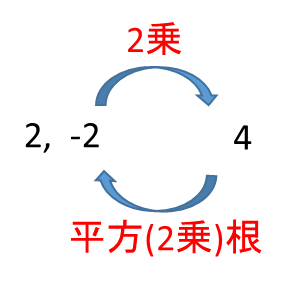
したがって, \(4\) の平方根は \(2\) , \(-2\) となります。
このように,正の数 \(a\) の平方根は 正と負の2つありますが, そのうち正の平方根を
\(\sqrt{a}\) (ルート \(a\) )
と表します。
例
\(4\) の平方根 → \(\pm 2\) ← 平方根の場合、 ± の 2 つあることに注意
\(\sqrt{4}\) → \(2\) ← 平方根のうち正の数のみ
根号を含む式の性質
根号を含む式には次の2つの性質があります。
① \(a \geq 0\) のとき \((\sqrt{a})^2 =(- \sqrt{a})^2 = a, \sqrt{a} \geq 0 \)
② \( \begin{eqnarray} \sqrt{a^2}=|a| = \begin{cases} a & (a \geq 0 のとき) \\ -a&(a \lt 0のとき) \end{cases}\end{eqnarray}\)
例題
次の値を求めよ。
① \((-\sqrt{7})^2\)
② \(\sqrt{9}\)
解答
① \((-\sqrt{7})^2=7\)
② \(\sqrt{9}=\sqrt{3^2}=3\)
 シンスケ
シンスケ基本的には2乗があればルートの外に出せると覚えておくといいでしょう。
根号含む式の計算公式
根号を含む式の計算公式には以下の3つがあります。
\(a>0, b>0, k>0 \) のとき
① \(\sqrt{a} \sqrt{b} = \sqrt{ab} \)
② \(\displaystyle\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\displaystyle\frac{a}{b}} \)
③ \(\sqrt{k^2 a} = k \sqrt{a} \)
例題
次の値を求めよ。
① \(\sqrt{3}\sqrt{5}\)
② \(\displaystyle\frac{\sqrt{24}}{\sqrt{8}}\)
③ \(\sqrt{20}\)
解答
① \(\sqrt{3}\sqrt{5}=\sqrt{3 \cdot 5}=\sqrt{15}\)
② \(\displaystyle\frac{\sqrt{24}}{\sqrt{8}}=\sqrt{\displaystyle\frac{24}{8}}=\sqrt{3}\)
③ \(\sqrt{20}=\sqrt{2^2 \cdot 5}=2\sqrt{5}\)
分母の有理化(単項式)
例えば、
\(\displaystyle\frac{5}{\sqrt{3}}\)
は分母と分子に \(\sqrt{3}\) をかけることで以下のように計算することができます。
\(\displaystyle\frac{5}{\sqrt{3}}\)
\(= \displaystyle\frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3} }\)
\(= \displaystyle\frac{5\sqrt{3}}{3}\)
このように分母に根号を含む式を変形して、分母に根号を含まない形に変形することを有理化するといいます。
分母の有理化(多項式)
分母が多項式の場合は分母の有理化は以下のように展開公式を利用することで有理化をすることができます。
\(\displaystyle\frac{\sqrt{3} – \sqrt{2} }{\sqrt{3} + \sqrt{2} }\)
\(= \displaystyle\frac{\sqrt{3} – \sqrt{2} }{\sqrt{3} + \sqrt{2} }\) \(\times\) \(\displaystyle\frac{\sqrt{3} – \sqrt{2} }{\sqrt{3} – \sqrt{2}}\)
\(= \displaystyle\frac{(\sqrt{3} – \sqrt{2})^2}{(\sqrt{3})^2 – (\sqrt{2})^2 }\)
\(= \displaystyle\frac{3 – 2\sqrt{6} + 2}{ 3 – 2 }\)
\(= 5 – 2\sqrt{6} \)




コメント