- 1次不等式とは
- 1次不等式の解き方
- 連立不等式の解き方
- A < B < C の形の連立不等式の解法
1次不等式の解き方~1次不等式とは,性質,基本的な解き方~
1次不等式とは
数の大小関係を
\(\lt\), \(\gt\), \(\leq\), \(\geq\)
のような不等号で表した式を不等式といいます。
例:不等式
ある数 \(x\) に \(3\) を加えた数は \(x\) の \(2\) 倍より小さい
⇒ \(x + 3 \lt 2x \)
ある数 \(x\) を \(5\) 倍して \(2\) を加えた数は \(- 3\) 以上である
⇒ \(5x + 2 \geq -3 \)
すべての項を移項して整理したとき,
\(ax + b \lt 0 \), \(ax + b \geq 0 \)
のように \(x\) の1次式になる不等式を\(x\) についての1次不等式といいます。
不等式の性質
不等式には以下の2つの性質が成り立ちます。
① \(A < B \) ならば \(A+C < B+C, A-C < B-C\)
② \(A < B\) ならば
\(C>0\) のとき \(AC < BC, \frac{A}{C} < \frac{B}{C} \)
\(C<0\) のとき \(AC > BC, \frac{A}{C} > \frac{B}{C} \)
例題
\(a>b\) のとき,次の▢に適する不等号\(>\)または\(<\)を答えよ。
\(2a+1\) ▢ \(2b+1\)
\(3-5a\) ▢ \(3-5b\)
解答
① \(a>b\) の両辺を\(2\)倍すると
\(2a>2b\)
両辺を\(+1\)すると
\(2a+1>2b\)
よって \(>\)
② \(a>b\) の両辺を\(-5\)倍すると
\(-5a<-5b\)
両辺を\(+3\)すると
\(3-5a<3-5b\)
よって \(<\)
 シンスケ
シンスケ特に、−をかける(で割る)ときは不等号の向きが逆になります。
注意しましょう。
1次不等式の解
\(x\) についての1次不等式を成り立たせるような \(x\) の値をその不等式の解といいます。
例:1次不等式の解
\(3 x > 2\) の解
⇒ \(x=1\) のとき (左辺)= 3 > 2 = (右辺)
より 不等式は成り立っているから、\(x = 1\) は不等式の解の1つ
※上記の他にも、\(x= 2\) , \(x= 3\), \(x= 5\) など上記を満たすものはすべて不等式の解
1次不等式の解き方
、不等式のすべての解を求めることを,その不等式を解くといいます。
STEP① 不等式を \(ax > b, ax \leq b \) などの形に整理する。
STEP② 整理された不等式の両辺を \(x\) の係数 \(a\) で割る。
例題
不等式 \(-3x+2>23\) を解け。
解答
\(-3x+2>23\)
\(-3x>23-2\)
\(-3x>21\)
よって、
\(x<-7\)



上記のような例題の場合 \(-7\) より小さい数はすべて解になることを表しています。
1次不等式の解き方~連立不等式の解き方~
いくつかの不等式を組み合わせたものを連立不等式といい、それらの不等式を同時に成り立たせる \(x\) の範囲を連立不等式の解といいます。また、連立不等式の解を求めることを連立不等式を解くといいます。
連立方程式の解法
連立方程式は以下のように解きます。
STEP① それぞれの不等式を解く
STEP② 解いた不等式の共通範囲を求める
例題
次の連立不等式を解け。
\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 1 > 9 \\
3x + 5 \leq 32
\end{array}
\right.
\end{eqnarray}
解答
\(2x + 1 > 9\) を解くと
\(x > 4 \) ……①
\(3x + 5 \leq 32\)を解くと
\(x \leq 9\) ……②
①、②より
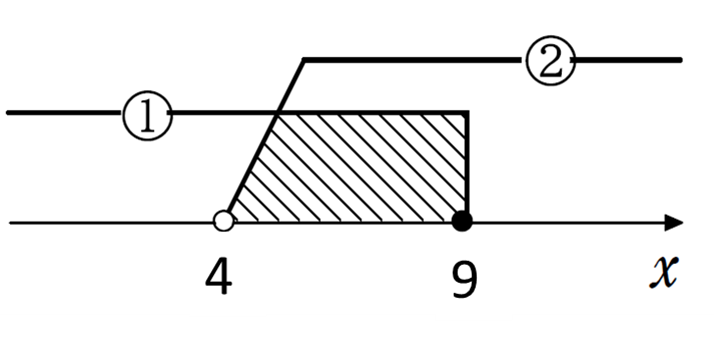

\(4 < x \leq 9\)
A < B < C の形の連立方程式の解法
\(A < B < C \)は, \(A < B\) かつ\(B < C\) が成り立つことと意味は同じになります。
例えば
\(2x – 1 < 3x < -x + 8\) であれば\(2x – 1 < 3x\) かつ\(3x < -x + 8\) となります。
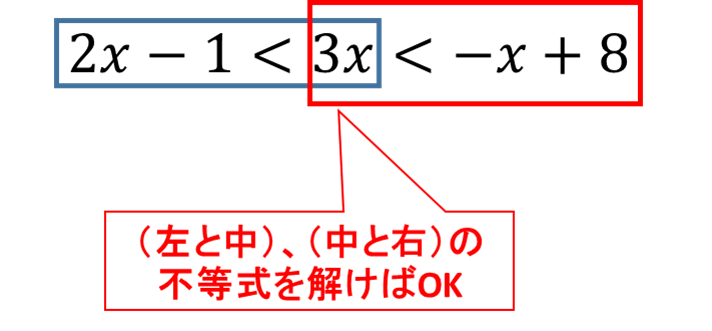




上図のように、(左と中)、(中と右)の不等式を解いて合わせればOKです。
したがって、以下のようになります。
\(2x – 1 < 3x < -x + 8\)
⇔ \(\begin{eqnarray}
\left\{
\begin{array}{l}
2x – 1 < 3x \\
3x < – x + 8
\end{array}
\right.
\end{eqnarray}\)
⇔
\(2x – 1 < 3x\) を解くと\(-1 < x\) …①
\(3x < -x + 8\) を解くと\(x < 2\) …②
①、②より
\(-1 < x < 2 \)



この形は一見すると連立不等式であることに気付きにくいので注意しましょう。






コメント