ここでは、【数学II】「指数・対数」でよく利用する公式(基礎知識)や例題を一覧にしてまとめています。
指数〜基本公式・例題一覧〜
1.累乗根の性質
\(a > 0, b > 0, m, n, p\) は正の整数とする。
- \((\sqrt[n]{a})^n = a\)
- \(\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{ab}\)
- \(\displaystyle\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\displaystyle\frac{a}{b}}\)
- \((\sqrt[n]{a})^m = \sqrt[n]{a^m}\)
- \(\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}\)
- \(\sqrt[n]{a^m} = \sqrt[np]{a^{mp}}\)
例題
次の計算をせよ。
(1)\((\sqrt[3]{2})^3\)
(2)\(\sqrt[3]{2}\sqrt[3]{4}\)
(3)\(\displaystyle\frac{\sqrt[3]{12}}{\sqrt[3]{2}}\)
(4)\((\sqrt[3]{2})^4\)
(5)\(\sqrt[3]{\sqrt{5}} \)
(6)\(\sqrt[10]{81}\)
解答
(1)\((\sqrt[3]{2})^3 = 2\)
(2)\(\sqrt[3]{2}\sqrt[3]{4} = \sqrt[3]{2 \times 4} = \sqrt[3]{8} = \sqrt[3]{2^3} = 2\)
(3)\(\displaystyle\frac{\sqrt[3]{12}}{\sqrt[3]{2}}=\sqrt[3]{\displaystyle\frac{12}{2}} = \sqrt[3]{6}\)
(4)\((\sqrt[3]{2})^4 = \sqrt[3]{2^4} = \sqrt[3]{16}\)
(5)\(\sqrt[3]{\sqrt{5}} = \sqrt[3 \times 2]{5} = \sqrt[6]{5}\)
(6)\(\sqrt[10]{3^4} = \sqrt[5 \times 2]{3^{2 \times 2}} = \sqrt[5]{3^2} = \sqrt[5]{9} \)
2.有理数の指数
\(a > 0 , m, n\) は正の整数, \(r\) は正の有理数とする
\(a^{\frac{m}{n}} = \sqrt[n]{a^m}\)
※特に、\(a^{\frac{1}{n}} = \sqrt[n]{a}\), \(a^{-r} = \displaystyle\frac{1}{a^r}\)
例題
(1)\(5^{\frac{2}{3}}\) を\(\sqrt[n]{a}\) の形に変形せよ。
(2)\(\sqrt[4]{8}\) を\(a^{\frac{m}{n}}\) の形に変形せよ。
解答
(1)\(5^{\frac{2}{3}} = \sqrt[3]{5^2} = \sqrt[3]{25}\)
(2)\(\sqrt[4]{8} = \sqrt[4]{2^3} = 2^{\frac{3}{4}}\)
3.指数法則
\(m , n \)は有理数とする。
① \(a^m \times a^n = a^{m+n}\)
② \((a^m)^n = a^{mn}\)
③ \((ab)^n =a^n b^n\)
※\(a^0 =1 \)
例題
次の計算をせよ。
① \(a^3 \times a^{-2} \)
② \((a^2)^{-3} \)
③ \((ab)^{-2} \)
解答
① \(a^3 \times a^{-2} = a^{3-2}=a \)
② \((a^2)^{-3} = a^{2 \times (-3)} =a^{-6} = \displaystyle\frac{1}{a^6}\)
③ \((ab)^{-2} = a^{-2} b^{-2} = \displaystyle\frac{1}{a^2b^2}\)
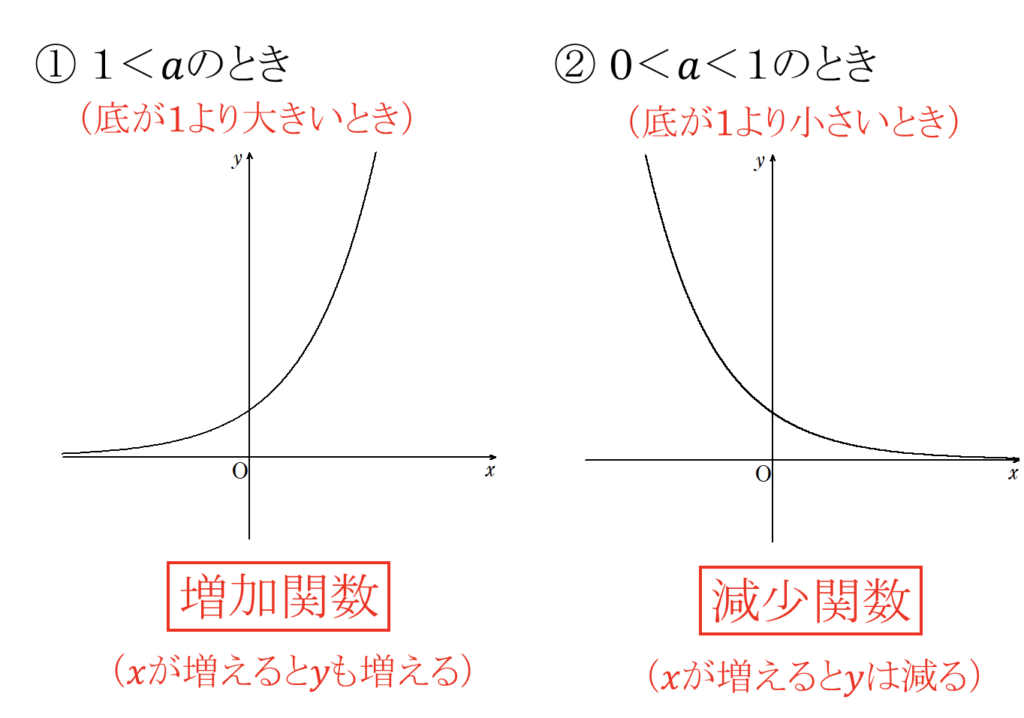
4.指数関数 \(y = a^x\) の性質
定義域:実数全体,値域:\(0 < y\)
①\(1 < a\)(底が1より大きい)とき
増加関数(\(x\)が増加すると\(y\)も増加)
②\(0 < a < 1\)(底が0より大きく、1より小さい)とき減少関数(\(x\)が減少すると\(y\)も減少)
例題
\(\sqrt{2} と \sqrt[3]{4} \) の大小を不等号を用いて表せ。
解答
\(\sqrt{2} = 2^{\frac{1}{2}}, \sqrt[3]{4} = \sqrt[3]{2^2} = 2^{\frac{2}{3}} \)
\(\displaystyle\frac{1}{2} < \displaystyle\frac{2}{3}\) であり,
底 が\(1\) より大きいので,
\(\sqrt{2} < \sqrt[3]{4} \)
対数〜基本公式・例題一覧〜
1.対数の定義
\(a > 0, a \neq 1, M > 0\) とする。
\(a^p = M ⇔ p = \log_a M\)
※「\(M\) は\(a\) の何乗か(指数の逆)」の値を表す
2.対数の性質
\(a > 0, a \neq 1, M > , N > 0, k\) :実数 とする。
- \(\log_a a = 1\), \(\log_a 1 =0\), \(\log_a \displaystyle \frac{1}{a} = -1\)
- \(\log_a M + \log_a N = \log_a MN\)
- \(\log_a M – \log_a N = \log_a \displaystyle\frac{M}{N}\)
- \(\log_a M^k =k \log_aM\)
例題
次の計算をし,簡単にせよ。
(1)\(\log_3 3\)
(2)\(\log_{10} 2 + \log_{10} 5 \)
(3)\(\log_3 7 – \log_3 63 \)
(4)\(2 \log_2 3 – \log_2 18\)
解答
(1)\(\log_3 3 = 1\)
(2)\(\log_{10} 2 + \log_{10} 5 = \log_{10} (2 \times 5) = \log_{10} 10 = 1\)
(3)\(\log_3 7 – \log_3 63\)
\(= \log_3 \displaystyle\frac{7}{63}\)
\(= \log_3 \displaystyle\frac{1}{9}\)
\( = \log_3 3^{-2}\)
\( = – 2\)
(4)\(2 \log_2 3 – \log_2 18\)
\(= \log_2 3^2 – \log_2 18\)
\(= \log_2 9 – \log_2 18\)
\(= \log_2 \displaystyle\frac{9}{18}\)
\(= \log_2 \displaystyle\frac{1}{2}\)
\(= \log_2 2^{-1}\)
\(= -1\)
3.底の変換公式
\(a > 0, b > 0, c > 0\) で,\(a \neq 1, b \neq 1, c \neq 1\) のとき,
\(\log_ab = \displaystyle\frac{\log_cb}{\log_ca}\)
特に、\(\log_ab = \displaystyle\frac{1}{\log_ba}\)
例題
\(\log_816\) を簡単にせよ。
解答
\(\log_816 = \displaystyle\frac{\log_216}{\log_28}\)
= \(\displaystyle\frac{\log_22^4}{\log_22^3}\)
= \(\displaystyle\frac{4}{3}\)
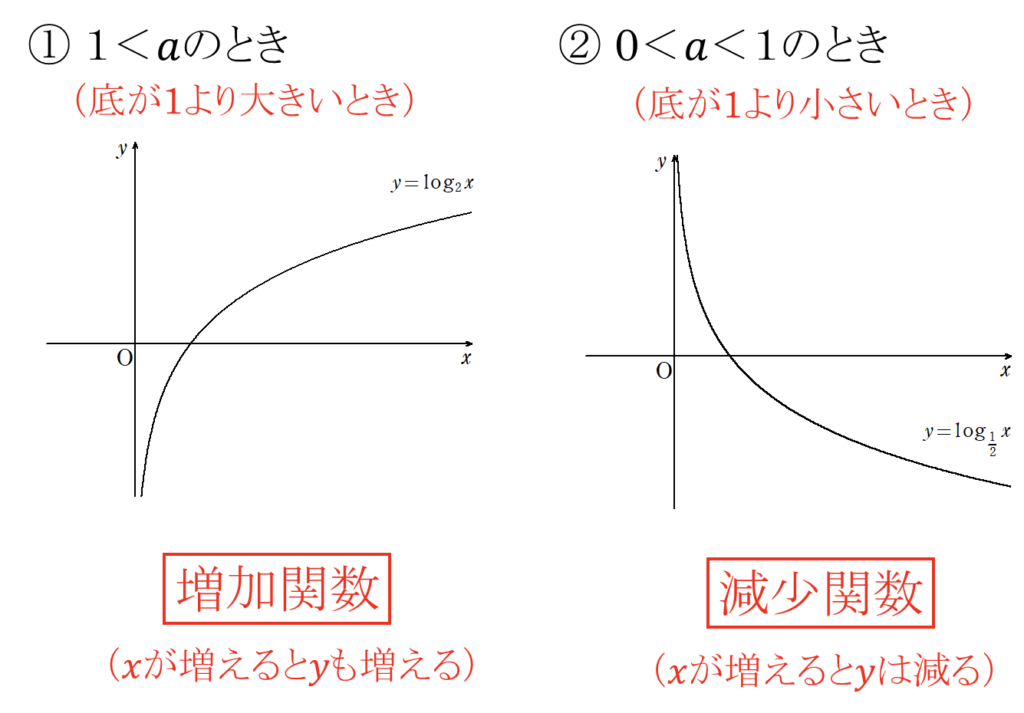
4.対数関数 \(y = \log_ax\) の性質
定義域:\(0 < x\),値域:実数全体
①\(1 < a\)(底が1より大きい)とき
増加関数(\(x\)が増加すると\(y\)も増加)
②\(0 < a < 1\)(底が0より大きく、1より小さい)とき減少関数(\(x\)が減少すると\(y\)も減少)
例題
\(\log_23 と \log_45 \) の大小を不等号を用いて表せ。
解答
\(\log_23 = \log_2\sqrt{9}\)
\(\log_45 = \displaystyle\frac{\log_25}{\log_24}\)
\(= \displaystyle\frac{\log_25}{\log_22^2}\)
\(= \displaystyle\frac{1}{2} \log_25\)
\(= \log_25^{\frac{1}{2}}\)
\(= \log_2\sqrt{5}\)
\(\sqrt{5} < \sqrt{9}\) であり,
底 が\(1\) より大きいので,
\(\log_45 < \log_23 \)
5.常用対数の利用
底が10 である対数を常用対数という
\(0 < x\) において
①\(n – 1 \leq \log_{10} x < n\)のとき、
\(x\) は\(n\)桁の整数
②\(-n \leq \log_{10} x < -(n-1) \)のとき、
\(x\) は小数第 \(n\) 位に初めて0でない数字が表れる
例題
\(3^{30}\) は何桁の整数か。ただし,\(\log_{10}3 = 0.4771\) とする。
解答
\(\log_{10}3^{30}\)
\(= 30 \log_{10}3\)
\(= 30 \times 0.4771\)
\(= 14.313\)
したがって,
\(14 \leq \log_{10}3^{30} < 15\)
よって,
\(15\) 桁





コメント