記事内に商品プロモーションを含む場合があります
 ラッシーくん
ラッシーくん数と式の分野が苦手なので、基本事項をマスターしたいです。
このような疑問や悩みに答えます。
数学Iの「数と式」分野は、高校数学のその他の単元でも多用する重要項目となっています。
この分野をマスターすることで、この後の分野が理解しやすくなったり、計算がスムーズになります。
この記事では、数学I「数と式」分野のまとめページとなっており、総復習をすることができます。
【数と式】単項式と多項式
単項式と多項式とは
数や文字を掛け合わせてできる式のことを単項式といいます。
単項式の例: \(3a^2 , -5x^2y\)
また、単項式において,数の部分を係数,かけ合わせた文字の個数を次数 といいます。
多項式とはいくつかの単項式の和の形で表される式のことをいいます。
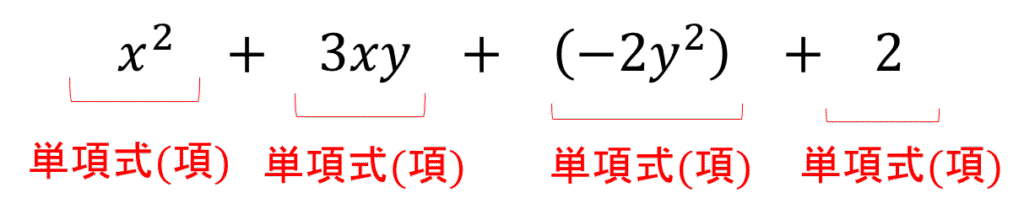
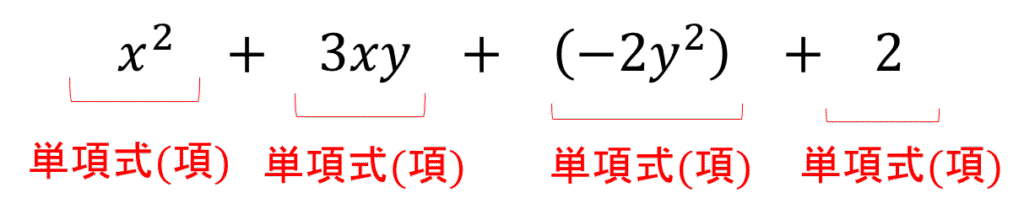
多項式のことを整式ともいいます。
例(多項式)
①\(2x^2 + 3x -1\)
② \(5x – 1\)
各単項式のことを多項式の項といいます。
また、多項式において、定数のみの(特定の文字を含まない)項のことを定数項といいます。
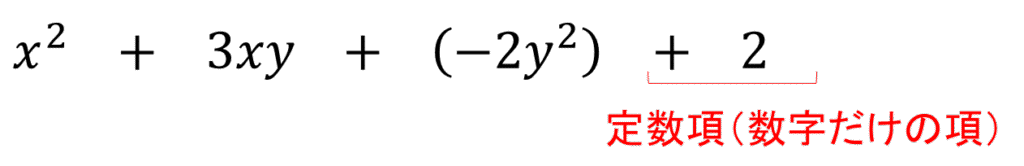
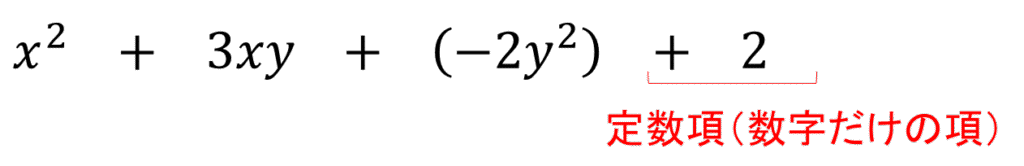
同類項の整理と降べきの順
多項式の項の中で文字の部分が全く同じ項のことを同類項といいます。
同類項どうしは1つにまとめて整理することができます。
例(同類項の整理)
① \(3x^2 – x + 2x^2 +2 -5x+3\)
\( = (3+2)x^2 +(-1-5)x+(2+3)\)
\(=5x^2-6x+5\)
② \(x^2 – 2x^2y^2 + 3x^2y^2 -5x^2+3y^2\)
\(=(1-5)x^2 +(-2+3)x^2y^2 +3y^2\)
\(=-4x^2+x^2y^2+3y^2\)
同類項を整理したとき、
項の次数が高い方から順に並べることを降べきの順に整理するといいます。
例(降べきの順に整理)
多項式\(2x-x^2+7+x^3+2x^4\)
降べきの順(次数の高い順)に整理(同類項をまとめる) ⇒ \(2x^4+x^3-x^2+2x+7\)
【数と式】多項式の計算規則・指数法則・展開公式
多項式の計算規則
多項式では、通常の数の計算と同様に次のような規則が成り立ちます。
\(A + B = B + A, AB = BA \)(交換法則)
\(A + B) + C = A + (B + C), (AB)C = A(BC)\) (結合法則)
\(A(B + C) = AB + AC , (A + B)C = AC + BC\)(分配法則)
指数法則
文字 \(a\) をいくつか掛けたものを \(a\) の累乗といい、\(n\)個掛けた場合は
\(a\)の\(n\)乗といい、\(a^n\)
のように表記します。
また、このときの\(n\)の部分を\(a^n\)の指数といいます。
指数に関しては以下の指数法則が成り立ちます。
\(m , n \)は正の整数とする。
① \(a^m \times a^n = a^{m+n}\) ⇒ 掛け算は足し算
② \((a^m)^n = a^{mn}\) ⇒ 指数乗は掛け算
③ \((ab)^n =a^n b^n\) ⇒ 指数乗は分配できる
※\(a^0 =1 \)
多項式の乗法
多項式\((a+b)\)と多項式 \((c+d)\)の乗法に関しては、
\(A(B + C) = AB + AC , (A+B)C = AC + BC\)(分配法則)
によって以下が成り立ちます。
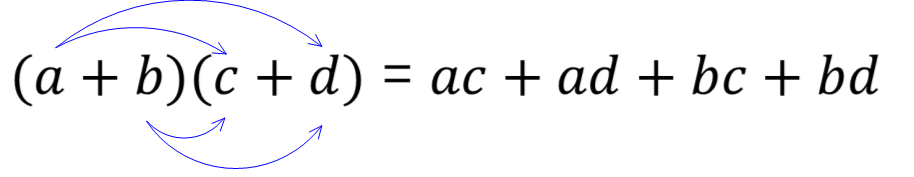
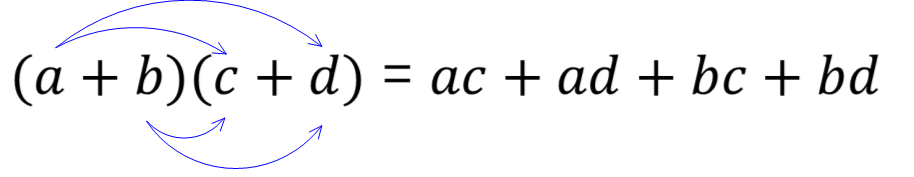
このように、多項式の積を計算して、同類項を整理し、単項式の和の形に表すことを式を展開するといいます。
展開公式
多項式の展開に関しては、特定の形をしている場合は以下の展開公式が成り立ちます。
①\((a+b)^2 = a^2 + 2ab + b^2\)
\((a-b)^2 = a^2 – 2ab + b^2 \)
②\((a+b) (a-b) = a^2 – b^2 \)
③\((x+a) (x+b) = x^2 + (a+b) x + ab \)
④\((ax+b)(cx+d) = acx^2 + (ad+bc) x + bd\)
\((a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca\)
【数と式】因数分解
因数分解とは
因数分解とは、簡潔にいえば、「展開の逆」になります。
\((x + 3) (x – 2) \) は展開すると,\(x^2 + x – 6\) になりますが,逆に,\(x^2 + x – 6\) は \((x + 3 ) (x – 2) \) に変形することができます。
このように,多項式を積の形に表すことを因数分解するといいます。
また、このときの積を作っている各多項式のことを因数といいます。
共通因数のくくり出し
各項に共通な因数(文字や数字)があれば、以下のようにくくり出しを行うことができます。
\(AB + AC = A (B+C) \)
因数分解の基本公式
基本的な展開公式の逆を考えることで、以下の因数分解の公式が得られます。
① \(a^2 + 2ab + b^2 = (a+b)^2 , a^2 – 2ab + b^2 = (a-b)^2 \)
② \(a^2 – b^2 = (a+b) (a-b) \)
③ \( x^2 + (a+b) x + ab = (x+a) (x+b)\)
④ \( acx^2 + (ad+bc) x + bd=(ax+b) (cx+d)\) ※たすきがけ
【数と式】実数
実数とは簡単にいうと
「数直線やグラフ上にかける数」
のことをいいます。
実数は大きく「有理数」と「無理数」の2つに分かれます。
全体的なイメージ
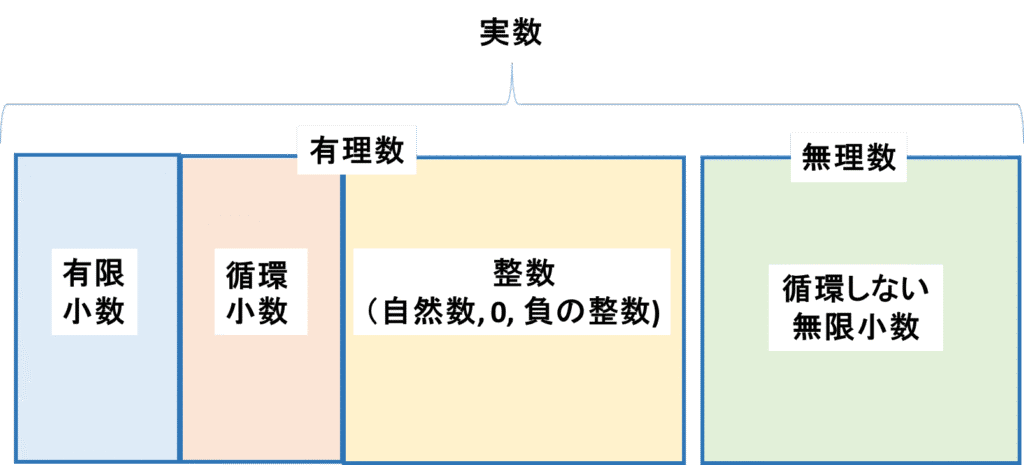

【数と式】根号を含む式の計算
平方根とは
例えば
\(2\) や \(-2\) は2乗すると\(4\)になるかと思いますが,逆に2乗して \(4\) になる数のことを \(4\) の平方(2乗)根といいます。
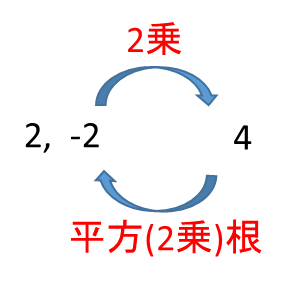

したがって, \(4\) の平方根は \(2\) , \(-2\) となります。
このように,正の数 \(a\) の平方根は 正と負の2つありますが, そのうち正の平方根を
\(\sqrt{a}\) (ルート \(a\) )
と表します。
① \(a \geq 0\) のとき \((\sqrt{a})^2 =(- \sqrt{a})^2 = a, \sqrt{a} \geq 0 \)
② \( \begin{eqnarray} \sqrt{a^2}=|a| = \begin{cases} a & (a \geq 0 のとき) \\ -a&(a \lt 0のとき) \end{cases}\end{eqnarray}\)
\(a>0, b>0, k>0 \) のとき
① \(\sqrt{a} \sqrt{b} = \sqrt{ab} \)
② \(\displaystyle\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\displaystyle\frac{a}{b}} \)
③ \(\sqrt{k^2 a} = k \sqrt{a} \)
分母の有理化
分母に根号を含む式を変形して、分母に根号を含まない形に変形することを有理化するといいます。
分母が多項式の場合は分母の有理化は以下のように展開公式を利用することで有理化をすることができます。
\(\displaystyle\frac{\sqrt{3} – \sqrt{2} }{\sqrt{3} + \sqrt{2} }\)
\(= \displaystyle\frac{\sqrt{3} – \sqrt{2} }{\sqrt{3} + \sqrt{2} }\) \(\times\) \(\displaystyle\frac{\sqrt{3} – \sqrt{2} }{\sqrt{3} – \sqrt{2}}\)
\(= \displaystyle\frac{(\sqrt{3} – \sqrt{2})^2}{(\sqrt{3})^2 – (\sqrt{2})^2 }\)
\(= \displaystyle\frac{3 – 2\sqrt{6} + 2}{ 3 – 2 }\)
\(= 5 – 2\sqrt{6} \)
【数と式】1次不等式の解き方
1次不等式と解法
数の大小関係を
\(\lt\), \(\gt\), \(\leq\), \(\geq\)
のような不等号で表した式を不等式といいます。
すべての項を移項して整理したとき,
\(ax + b \lt 0 \), \(ax + b \geq 0 \)
のように \(x\) の1次式になる不等式を\(x\) についての1次不等式といいます。
① \(A < B \) ならば \(A+C < B+C, A-C < B-C\)
② \(A < B\) ならば
\(C>0\) のとき \(AC < BC, \frac{A}{C} < \frac{B}{C} \)
\(C<0\) のとき \(AC > BC, \frac{A}{C} > \frac{B}{C} \)
\(x\) についての1次不等式を成り立たせるような \(x\) の値をその不等式の解といいます。
不等式のすべての解を求めることを,その不等式を解くといいます。
STEP① 不等式を \(ax > b, ax \leq b \) などの形に整理する。
STEP② 整理された不等式の両辺を \(x\) の係数 \(a\) で割る。
連立不等式の解法
いくつかの不等式を組み合わせたものを連立不等式といい、それらの不等式を同時に成り立たせる \(x\) の範囲を連立不等式の解といいます。また、連立不等式の解を求めることを連立不等式を解くといいます
STEP① それぞれの不等式を解く
STEP② 解いた不等式の共通範囲を求める
【数と式】絶対値を含む方程式・不等式の解き方
絶対値とは
数直線上における原点\(O(0)\) と点\(P(a)\) との距離を,実数\(a\) の絶対値といい、
実数\(a\) の絶対値であれば \(|a|\)
と表します。
絶対値の外し方
絶対値の中が正 → そのまま外す
絶対値の中が負 → −をつけて外す
\( \begin{eqnarray} |x| = \begin{cases} x & (x \geq 0 のとき) \\ -x&(x \lt 0のとき) \end{cases}\end{eqnarray}\)
\(c\) が正の定数のとき
① 方程式 \(|x|=c\) の解は \(x=\pm c \)
② 不等式 \(|x|<c\) の解は \(-c<x<c\)
③ 不等式 \(|x|>c\) の解は \(x<-c, c<x \)
【数と式】基本公式集・記事まとめ
以下で「数と式」公式集と解説記事をまとめています。
以下で「数と式」の基本問題のまとめを解くことができます。定着させるにはこちらがおすすめです。





コメント