関数とは
\(x\) の値を定めるとそれに対応して\(y\) の値がただ1つ定まるとき, \(y\) は \(x\) の関数といいます。
例えば
\(y = 3x + 1\)
は\(x\) の値を1つ定めると\(y\) の値がただ1つ定まるので\(y\) は \(x\) の関数です。
\(y = 3x + 1\) のように\(x\) の1次式で表される関数を\(x\) の1次関数といいます。
1次関数のグラフの書き方はこちら
1次関数は\(a\), \(b\) を定数として一般に次の形で表されます。
\(y = ax + b\) \((a \neq 0)\)
2次関数のグラフの書き方
\(x\) の2次式で表される関数を\(x\) の2次関数といいます。
2次関数は\(a\), \(b\) , \(c\) を定数として一般に次の形で表されます。
\(y = ax^2 + bx + c\) \((a \neq 0)\)
2次関数\(y = ax^2\)のグラフの書き方
まず、\(y = ax^2\) のグラフを考えてみましょう。
一般に、2次関数\(y = ax^2\) のグラフは, 原点\(O\) を通り, \(y\) 軸に関して対称な曲線となります。
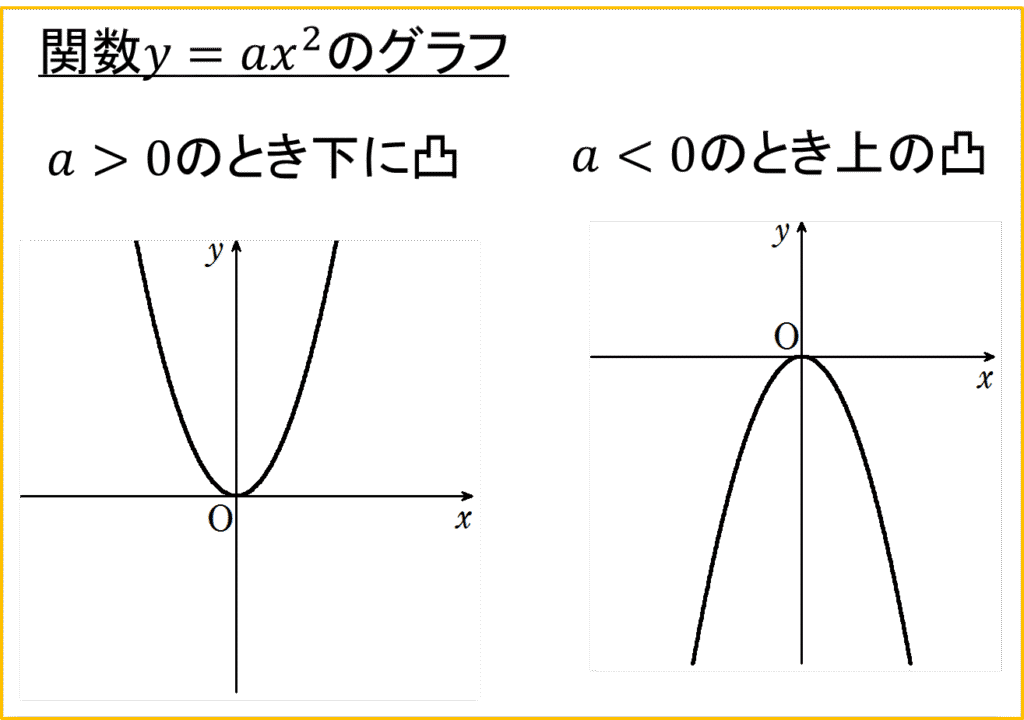
上記のように、2次関数\(y = ax^2\) のグラフは\(a\) の値の符号によって、2種類存在します。
このグラフの形の曲線を放物線といい、放物線は対称の軸を必ずもっています。
この対称の軸のことを、その放物線の軸といい、軸と放物線の交点を,その放物線の頂点といいます。
2次関数\(y = ax^2\) のグラフの場合は、軸が\(y\) 軸, 頂点が原点の放物線となります。
2次関数\(y = a(x – p)^2 + q\) のグラフの書き方
続いて、\(y = a(x – p)^2 + q\) のグラフを考えてみましょう。
例えば、\(y = 2(x – 3)^2 + 4\)のグラフは値を調べると以下のようになります。
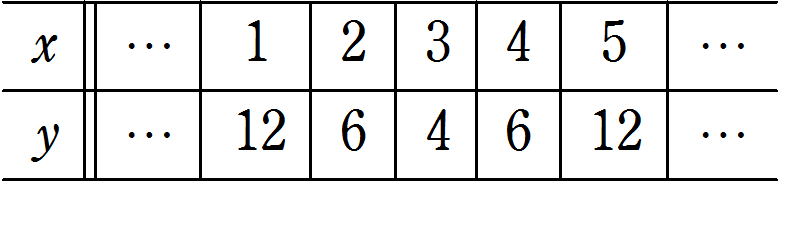
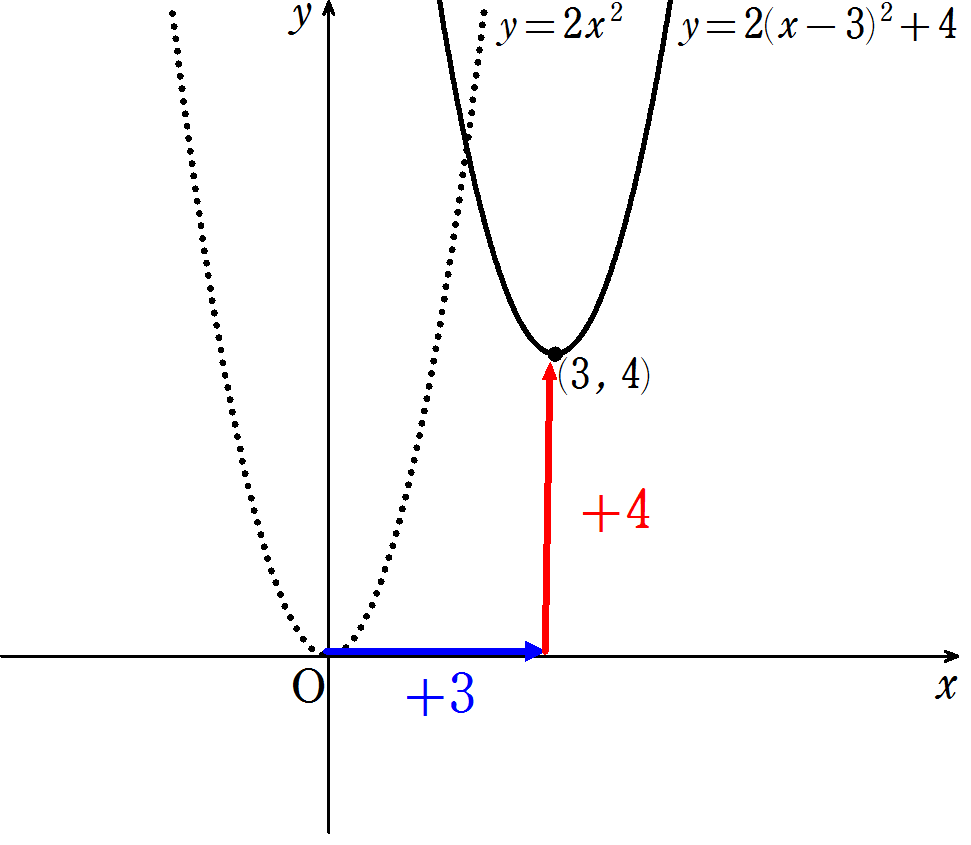
すなわち、\(y = 2x^2\) のグラフを \(x\) 軸方向に \(3\) , \(y\) 軸方向に \(4\) だけ平行移動した放物線となります。
つまり、この放物線の頂点は\((3, 4)\) , 軸は直線 \(x = 3\) となります。
一般に、2次関数 \(y = a(x – p)^2 + q\) は次のことがいえます。
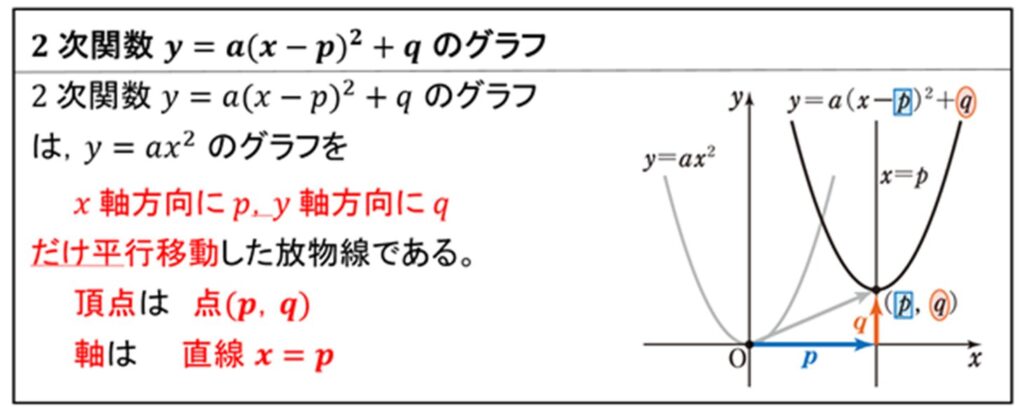
したがって、このことを活用すると、以下の手順により \( y = a(x – p)^2 + q\) のグラフを書くことができます。
- 頂点・軸を求める
- 頂点・\(y\) 切片をとる
- グラフの概形を書く
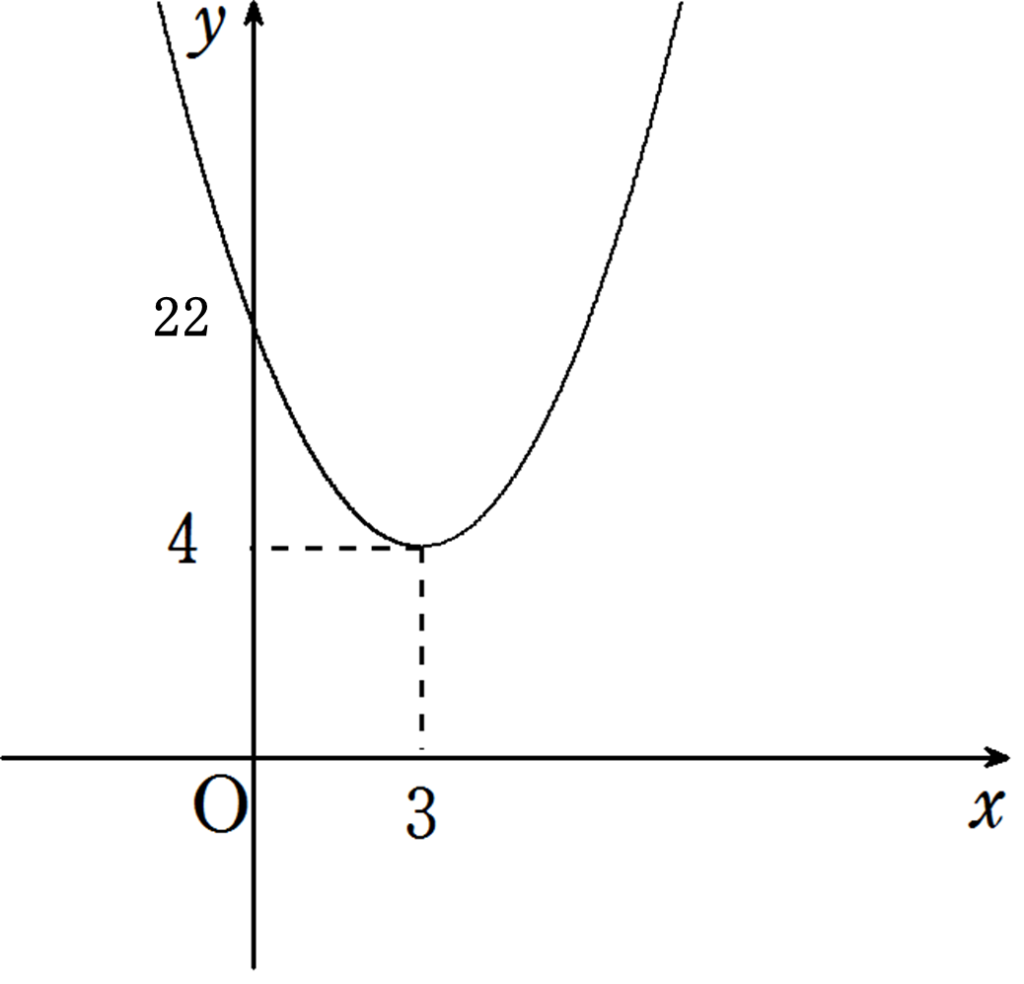
例題 2次関数\(y = 2(x – 3)^2 + 4\) の頂点と軸を求めよ。
頂点は点 \((3 , 4)\) , 軸は直線\(x = 3\)
\(y\) 切片は
\(x = 0\) のとき \(y = 2(0 – 3)^2 + 4 = 22
2次関数\(y = ax^2 + bx + c\) のグラフの書き方
続いて、\(y = ax^2 + bx + c\) のグラフを考えてみましょう。
結論、これは \( y = a(x – p)^2 + q\) の 形に変形することで2次関数のグラフをかくことができます。
このような変形をすることを平方完成するといいます。
平方完成
基本的な平方完成は2乗の展開公式
\((x – p)^2 = x^2 -2px + p^2\) より

例題 \(2x^2 – 4x + 1\) の平方完成をせよ。
\(2x^2 – 4x + 1\)
\(= 2(x^2 – 2x) + 1\)
\(= 2\{(x – 1)^2 – 1^2\} + 1\)
\(= 2(x – 1)^2 – 2\times 1^2 + 1\)
\(= 2(x – 1)^2 – 1\)
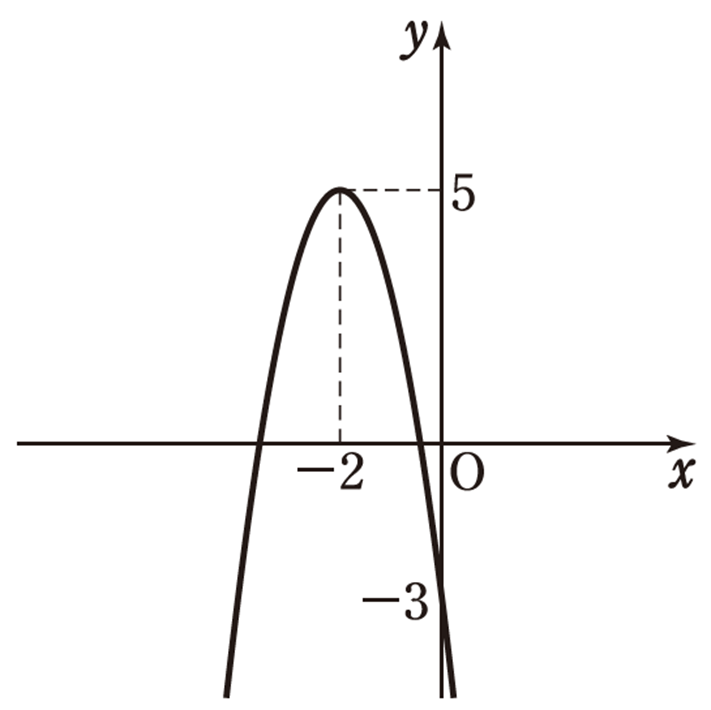
例題 \(y = -2x^2 – 8x – 3\) のグラフをかけ。また, その頂点と軸を求めよ。
\(-2x^2 – 8x – 3\)
\(= -2(x^2 + 4x) – 3\)
\(= -2\{(x + 2)^2 – 2^2\} – 3\)
\(= -2(x + 2)^2 + 5
よって、
頂点\((-2, 5)\), 直線\(x = -2\)






コメント