記事内に商品プロモーションを含む場合があります
平面上で、図形上の各点を一定の向きに,一定の距離だけ動かすことを平行移動といいます。
この記事では2次関数に関する平行移動の問題の解き方について解説していきます。
2次関数の平行移動の解き方
2次関数の平行移動の問題の解き方は大きく以下の2パターンがあります。
パターン①:頂点の移動を考える方法
パターン②:\(x\) と \(y\) の値をおき換える方法
例えば、以下のような問題について、解法をみていきましょう。
例題 放物線 \(y = x^2 – 2x + 3\) を, \(x\) 軸方向に \(2\), \(y\) 軸方向に \(-3\) だけ平行移動して得られる放物線の方程式を求めよ。
パターン①:頂点の移動を考える方法
1つ目の解法は「頂点の移動を考える方法」です。
一般に、2次関数 \(y = a(x – p)^2 + q\) については次のことがいえます。
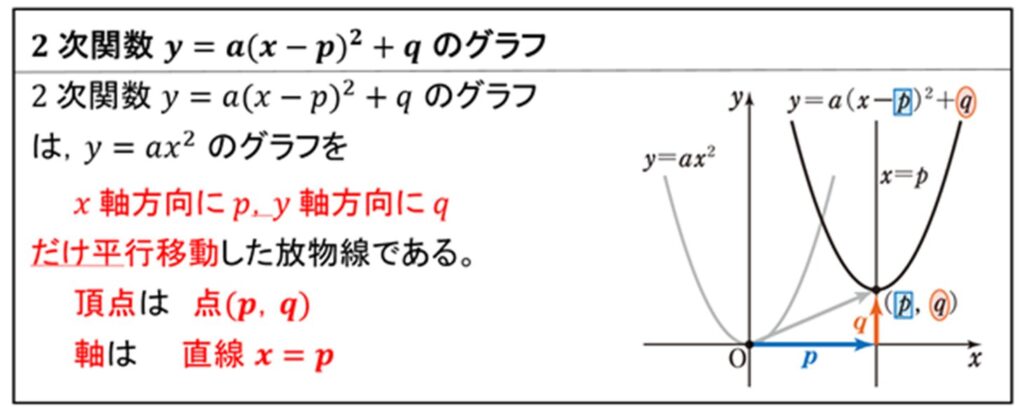

このことを活用すると、以下の手順により、例題を解くことができます。
例題 放物線 \(y = x^2 – 2x + 3\) を, \(x\) 軸方向に \(2\), \(y\) 軸方向に \(-3\) だけ平行移動して得られる放物線の方程式を求めよ。
\(y = x^2 – 2x +3 = (x-1)^2 + 2\)
より 頂点 \((1, 2)\) ← 移動前の放物線の頂点を求める
したがって、\(x\) 軸方向に \(2\) , \(y\) 軸方向に \(-3\) だけ平行移動した頂点の座標は
\((1 + 2, 2 – 3) = (3, -1)\) ← 移動前の放物線の頂点から移動後の頂点を求める
よって、求める放物線の方程式は
\(y = (x -3)^2 – 1\) ← 頂点がわかれば、移動後の放物線の方程式がわかる
すなわち
\(y = x^2 – 6x + 8\)
 シンスケ
シンスケ上記のように、2次関数の場合は頂点に着目をして、移動後の頂点を求めることで、簡単に求めることができます。
パターン②:\(x\) と \(y\) の値をおき換える方法
2つ目の解法は「\(x\) と \(y\) の値をおき換える方法」です。


上記の通り、
\(y = a(x – p)^2 + q\) すなわち\(y – q = a(x – p)^2\) のグラフは \(y ax^2\) のグラフを\(x\) 軸方向に \(p\) ,\(y\) 軸方向に \(q\) だけ平行移動した放物線ですね。
このことは、逆も明らかに成り立つため、
一般に、\(x\) を \(x – p\), \(y\) を \(y – q\) だけ平行移動した放物線は\(x\) を \(x – p\), \(y\) を \(y – q\) でおき換えればよいことがわかります。
\(y = ax^2 + bx + c\)
を\(F\) とし, \(F\) を\(x\) 軸方向に \(p\) , \(y\) 軸方向に \(q\) だけ平行移動して得られる放物線を\(G\) とすると, \(G\) の方程式は
①において
\(x\) を \(x – p\) , \(y\) を \(y – q\) でおき換えた式
\(\color{red}{y – q = a(x – p)^2 + b(x – p) + c}\)
になる。
このことをふまえると、例題は以下のように解くことができます。
例題 放物線 \(y = x^2 – 2x + 3\) を, \(x\) 軸方向に \(2\), \(y\) 軸方向に \(-3\) だけ平行移動して得られる放物線の方程式を求めよ。
\(y = x^2 – 2x + 3\) の \(x\) を \(x – 2\), \(y\) を \(y – (-3)\) でおき換えると
\(y – (-3) = (x – 2)^2 – 2(x – 2) + 3\)
よって、求める放物線の方程式は
\(y = x^2 – 6x + 8\)



この方法はおき換えるだけなので、「パターン①:頂点を求める方法」よりも比較的早く計算することができます。
しかしながら、「パターン①」ではないと解けない問題もありますので、使い分けが大切です。





コメント