目次
1次関数のグラフ
関数のグラフ
一般に,関数\(y = f(x)\) が与えられたとき,関数 \( y = f(x)\) を満たすような点\((x , y)\) , すなわち点\((x, f(x))\)全体で作られる図形を、この関数のグラフといいます。
 シンスケ
シンスケすなわち、グラフとはあくまでも「点の集まり」になります。
関数とそのグラフについて、次が成り立ちます。
関数 \(y = f(x)\)上の点の性質
点\((a, b)\) が関数 \(y = f(x)\) のグラフ上にある
\(\iff\) \(b = f(a)\)



点がグラフ上にある(通る)ときは、代入してOKということを覚えておきましょう。
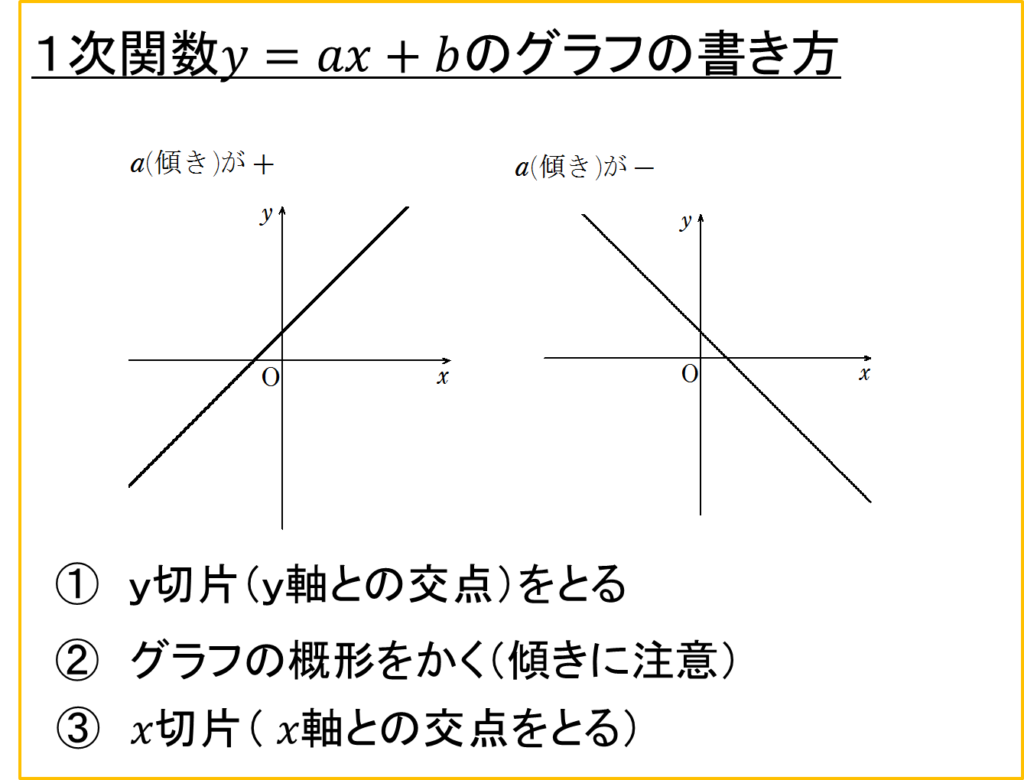
1次関数のグラフ
1次関数\(y = ax + b\) のグラフは以下の手順で書くことができます。
1次関数のグラフの書き方
- \(y\) 切片(\(y\) 軸との交点)をとる
- グラフの概形をかく(傾きに注意)
- \(x\) 切片(\(x\) 軸との交点)をとる

例題
関数 \(y = 2x – 7\) \((1 < x \leq 4)\) の値域および、最大値、最小値を求めよ。
解答
この関数のグラフは以下のようになる。
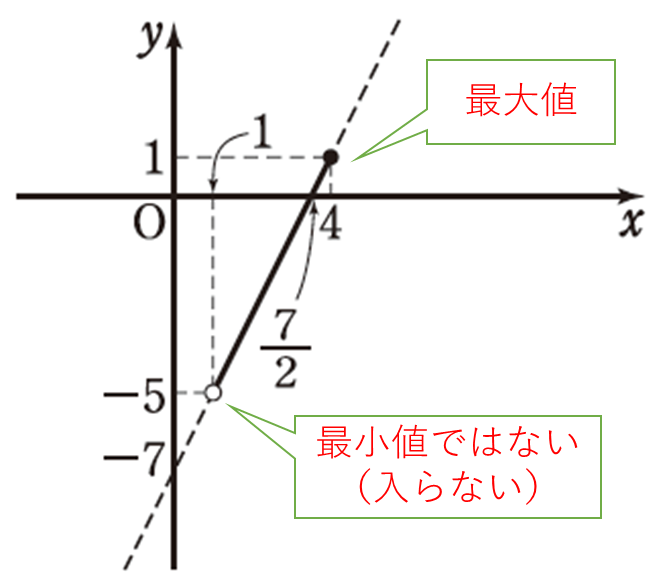

よって、この関数の値域は \(-5 < y \leq 1\)
また、この関数は
\(x = 4\) で最大値\(1\)
最小値はなし



\(y\) は\(-5\) にいくらでも近い値をとるが、どのような\(x\) の値に対しても\(y = -5\) にはならないため、上記の場合、最小値はありません。





コメント