記事内に商品プロモーションを含む場合があります
この記事では、「頂点」「軸」「グラフ上の3点」など、特定の条件が与えられたときの2次関数の決定の問題について解説していきます。
2次関数の決定
以下のような例題について考えてみましょう。
例題 次の条件を満たす放物線をグラフにもつ2次関数を求めよ。
(1) 頂点が点\((1, 2)\) で, 点\((3, 6)\) を通る。
(2) 軸が直線 \(x = -1\) で, 2点 \((1, 3)\), \((-2, -3)\) を通る。
(3) 放物線\(y =x^2\) を平行移動したもので、点(1, -1) を通り、その頂点は直線\(y= 4x -1\) 上にある。
(4) \(x = 2\) のとき最大値 \(3\) をとり, 点\((1,2)\) を通る。
(5) 3点\((1, -2), (-2, -5), (3, 10)\) を通る。
(6) \(x\) 軸との交点が\((1, 0), (3, 0)\) であり, 点\((4, 3)\) を通る。
2次関数のおき方
数学では上記のような「~の値を求めよ。」という形式の問題が多く出題されます。
求めるものは「値」「関数」など様々ですが、原則的にはこのような場合は
「求めたい値を文字でおく」
というのが基本方針となります。
ただの「値」の場合のおき方は単純に「\(x\)」「\(a\)」などでおけばよいのですが、2次関数のおき方は以下の3種類の形があります。
①(標準形)\(y = a(x – p)^2 + q\)
\(\iff\) 頂点・軸・最大値・最小値関連の場合
②(一般形)\(y = ax^2 + bx + c\)
\(\iff\) 通る3点がわかっている、微分・積分関連の場合
③(分解形)\(y = a(x – \alpha) (x – \beta)\)
\(\iff\) \(x\) 軸との交点がわかっている場合
 シンスケ
シンスケ上記のどのおき方がよいかは、問題にもよります。
問題のタイプによって、使い分けることが大切です。
(標準形)\(y = a(x – p)^2 + q\) でおくタイプの問題
まずは、「\(y = a(x – p)^2 + q\) でおくタイプの問題」をみていきましょう。
\(y = a(x – p)^2 + q\) はそもそも以下のように、\(y = ax^2\) のグラフを\(x\)軸方向に\(p\),\(y\)軸方向に\(q\) だけ平行移動した放物線であるため、頂点や軸がわかるところが大きな特徴でした。
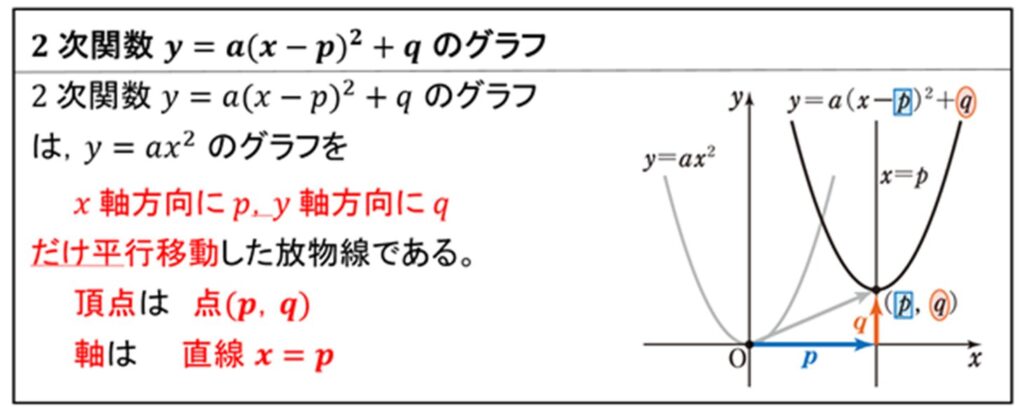

したがって、\(y = a(x – p)^2 + q\) でおくタイプの問題は結論
「頂点」「軸」関連の情報がわかっているときに利用する
と覚えておくとよいでしょう。
具体的には以下のような問題になります。
頂点がわかっている問題
例題 次の条件を満たす放物線をグラフにもつ2次関数を求めよ。
(1) 頂点が点\((1, 2)\) で, 点\((3, 6)\) を通る。
求める2次関数を
\(y = a(x – p)^2 + q \) ← 頂点の座標がわかっているときは標準形
とおく
頂点が\((1, 2)\) つまり、\(p = 1, q = 2\) であるから
\(y = a(x – 1)^2 + 2\) ← 頂点の座標がわかる場合はいきなりこの形式でおくのが一般的
と表せる
これが点\((3, 6)\) を通るから
\(6 = a(3 – 1)^2 + 2\) ← 通るときは代入してOK
これを解くと
\(a = 1\)
したがって、求める2次関数は
\(y = (x – 1)^2 + 2\)
\((y = x^2 -2x + 3 を答えとしてもよい)\)
軸がわかっている問題
例題 次の条件を満たす放物線をグラフにもつ2次関数を求めよ。
(2) 軸が直線 \(x = -1\) で, 2点 \((1, 3)\), \((-2, -3)\) を通る。
求める2次関数を
\(y = a(x – p)^2 + q \) ← 軸の方程式がわかっているときは標準形
とおく
軸が直線\(x = -1\) つまり、\(p = -1\) であるから
\(y = a(x + 1)^2 + q\) ← 軸の方程式がわかる場合はいきなりこの形式でおくのが一般的
と表せる
これが点\((1, 3), (-2, -3)\) を通るから ← 通るときは代入してOK
\(3 = a(1 + 1)^2 + q\) ……①
\(-3 = a(-2 + 1)^2 + q\) ……②
①、②を解くと
\(a = 2, q = -5\)
したがって、求める2次関数は
\(y = 2(x + 1)^2 – 5\)
頂点の関係式がわかっている問題
例題 次の条件を満たす放物線をグラフにもつ2次関数を求めよ。
(3) 放物線\(y =x^2\) を平行移動したもので、点(1, -1) を通り、その頂点は直線\(y= 4x -1\) 上にある。
求める2次関数を
\(y = a(x – p)^2 + q \) ← 頂点の座標の関係式がわかっているときも標準形でOK
とおく
求める放物線は\(y = x^2\) を平行移動したものより、 \(a = 1\)
また、頂点\((p, q)\) は直線\(y = 4x – 1\) 上にあるから、
\(q = 4p – 1\)
したがって、求める2次関数は
\(y = (x – p)^2 + 4p – 1\) ← いきなりこの形式でおいてもOK
と表せる
これが、点\((1, -1)\) を通るから
\(-1 = (1 – p)^2 + 4p – 1\)
これを解くと
\(p = -1\)
したがって、求める2次関数は
\(y = (x + 1)^2 – 5\)
最大値・最小値がわかっている問題
少し応用問題になりますが、2次関数は最小値や最大値は原則、「頂点」or「端点(定義域の制限がある場合のみ)」でしかとりません。
したがって、以下のように最大値・最小値がわかっている問題は頂点関連であるため、原則的には標準形でおきます。
例題 次の条件を満たす放物線をグラフにもつ2次関数を求めよ。
(4) \(x = 2\) のとき最大値 \(3\) をとり, 点\((1,2)\) を通る。
求める2次関数を
\(y = a(x – p)^2 + q \) ← 最大値・最小値がわかっているときも標準形でおく
とおく
\(x = 2\) のとき 最大値\(3\) をとるから
頂点が\((2, 3)\) より
\(y = a(x – 2)^2 + 3\) ← いきなりこの形式でおいてもOK
これが、点\((1, 2)\) を通るから
\(2 = a(1 – 2)^2 + 3\)
これを解くと
\(a = -1\)
したがって、求める2次関数は
\(y = -(x – 2)^2 + 3\)
(一般形)\(y = ax^2 + bx + c\) でおくタイプの問題
続いて、「\(y = ax^2 + bx + c\) でおくタイプの問題」をみていきましょう。
この関数の特徴は\(y = a(x – p)^2 + q\) と比較して、代入しやすい(代入したときの結果が簡単になりやすい)という点があります。
したがって、数学Ⅰの範囲では主に
「通る3点」がわかっているときに利用する
と覚えておくとよいでしょう。
※ただし、数学IAⅡBまでの範囲の場合は「微分・積分」においても原則一般形でおきます。
例題 次の条件を満たす放物線をグラフにもつ2次関数を求めよ。
(5) 3点\((1, -2), (-2, -5), (3, 10)\) を通る。
求める2次関数を
\(y = ax^2 + bx^2 + c \) ← グラフ上の通る3点がわかる場合は一般形でおく
とおく
これが、3点\((1, -2), (-2, -5), (3, 10)\) を通るから
\begin{eqnarray}
\left\{
\begin{array}{l}
-2 = a \cdot 1^2 + b \cdot 1 + c ……①\\
-5 = a \cdot (-2)^2 + b \cdot (-2) + c ……② \\
10 = a \cdot 3^2 + b \cdot 3 + c ……③
\end{array}
\right.
\end{eqnarray}
したがって、
\begin{eqnarray}
\left\{
\begin{array}{l}
-2 = a + b + c ……①\\
-5 = 4a – 2b + c ……② \\
10 = 9a + 3b + c ……③
\end{array}
\right.
\end{eqnarray}
①、②、③を解くと
\(a = -1, b = 4, c = 6\)
したがって、求める2次関数は
\(y = – x^2 + 4x + 6\)
(分解形)\(y = a(x – \alpha) (x – \beta)\) でおくタイプの問題
最後に、「\(y = a(x – \alpha) (x – \beta)\) でおくタイプの問題」をみていきましょう。
この分解形のように因数分解されている場合は、\(y = 0\) としたときの解が
\(x = \alpha, \beta\)
となるため、 \(x\) 軸との交点がわかることにあります。
したがって、
「\(x\)軸との交点」がわかっているときに利用する
と覚えておくとよいでしょう。
逆にいうと、これ以外のパターンではほとんど利用しませんので、3種類の中では最も利用頻度は低くなります。
例題 次の条件を満たす放物線をグラフにもつ2次関数を求めよ。
(6) \(x\) 軸との交点が\((1, 0), (3, 0)\) であり, 点\((4, 3)\) を通る。
求める2次関数を
\(y = a(x – \alpha) (x – \beta)\) ← x軸との交点がわかる場合は分解形でおく
とおく
\(x\) 軸との交点が\((1, 0), (3, 0)\) であるから
\(\alpha = 1, \beta = 3\)
であるため、
\(y = a(x – 1) (x – 3)\) ← いきなりこの形式でおいてもOK
これが、点\((4, 3)\) を通るので
\(3 = a(4 – 1) (4 – 3)\)
これを解くと、
\(a = 1\)
したがって、求める2次関数は
\(y = (x – 1) (x – 3)\)






コメント