ここでは、【数学A】でよく利用する公式(基礎知識)一覧にしてまとめています。
【数学A】公式集~場合の数と確率~
【場合の数と確率】1.集合の要素の個数
\(U\)を全体集合とし,\(A, B\)をその部分集合とする。
①\(n(A \cup B)=n(A)+n(B)-n(A \cap B)\)
②\(A \cap B = \emptyset \) のとき \(n(A \cup B) =n(A)+n(B)\)
\(n(\overline{A})=n(U)-n(A)\)
【場合の数と確率】2.場合の数
2つの事柄A, Bは同時には起こらないとする。
Aの起こり方が\(a\)通りあり,Bの起こり方が\(b\)通りあるとすると,AまたはBの起こる場合の数は
\(a+b\) 通り
事柄A の起こり方が\(a\)通りあり,そのおのおのの場合について,事柄B の起こり方が\(b\)通りあるとすると,AとBがともに起こる場合の数は
\(a \times b\) 通り
【場合の数と確率】3.順列
異なる\(n\)個のものから\(r\)個選んで並べる場合の総数は
\({}_n P_r =n(n-1)(n-2) \cdots\cdots (n-r+1)\) 通り
異なる\(n\)個のものをすべて並べる場合の総数は
\(n! = n(n-1)(n-2) \cdots\cdots \cdot 3 \cdot 2 \cdot 1 \) 通り
【場合の数と確率】4.円順列
異なる\(n\)個のものの円順列の総数は
\((n-1)!\)
【場合の数と確率】5.組合せ
① \({}_n C_r\)
\(=\frac{{}_n P_{n-r}}{r!}\)
\(=\frac{n(n-1)(n-2) \cdots\cdots (n-r+1)}{r(r-1)\cdots\cdots\cdot 3 \cdot 2 \cdot 1}\)
② \({}_n C_r = \frac{n!}{r!(n-r)!}\) \((0!=1, {}_n C_0 =1)\)
① \({}_n C_r = {}_n C_{n-r}\) \((ただし、0 \leq r \leq n)\)
② \({}_n C_r = {}_{n-1} C_{r-1}+{}_{n-1}C_r\) \((ただし、1 \leq r \leq n-1, n \geq 2)\)
【場合の数と確率】6.同じものを含む順列
aが\(p\)個, bが\(q\)個,c が\(r\)個あるとき,それら全部を1列に並べる順列の総数は
\({}_n C_p \times {}_{n-p}C_q = \frac{n!}{p!q!r!}\) \((ただし、p+q+r=n)\)
【場合の数と確率】7.事象と確率
全事象\(U\)のどの根元事象も同様に確からしいとき,
事象\(A\)の起こる確率\(P(A)\)は
\(P(A)=\frac{n(A)}{n(U)}\)
【場合の数と確率】8.いろいろな事象
2つの事象を\(A,B\)とする。
\(A\)と\(B\)がともに起こる事象
\(A\)または\(B\)のどちらか一方が起こる事象
空集合\(\emptyset\)で表される事象
2つの事象\(A, B\)が同時に起こらないとき,\(A, B\)は互いに排反または、互いに排反事象であるという。
【場合の数と確率】9.確率の基本性質
① \(0 \leq P(A) \leq 1\)
② 空事象\(\emptyset\)の確率:\(P(\emptyset)=0\)
③ 全事象\(U\)の確率:\(P(U)=1\)
④ 事象\(A, B\)が互いに排反であるとき \(P(A \cup B)=P(A)+P(B) \)
【場合の数と確率】10.和事象の確率
\(P(A \cup B)=P(A)+P(B)-P(A \cap B)\)
※特に, \(A \cap B=\emptyset\)のとき \(P(A \cup B)=P(A)+P(B)\)
【場合の数と確率】11.余事象の確率
\(P(\overline{A})=1-P(A)\)
【場合の数と確率】12.独立な試行の確率
2つの試行SとTが独立であるとき,Sで事象\(A\)が起こり,かつTで事象\(B\)が起こる確率\(p\)は,
\(p=P(A)P(B)\)
【場合の数と確率】13.反復試行の確率
1回の試行で事象\(A\)の起こる確率を\(p\)とする。この試行を\(n\)回行う反復試行で,
\(A\)がちょうど\(r\)回起こる確率は
\({}_n C_r p^r (1-p)^{n-r}\)
【場合の数と確率】14.条件付き確率
事象\(A\)が起こったときの事象\(B\)の起こる確率は
\(P_A(B)=\frac{P(A \cap B)}{P(A)}\)
【場合の数と確率】15.確率の乗法定理
2つの事象\(A, B\)がともに起こる確率は
\(P(A \cap B)=P(A)P_A(B)\))
【場合の数と確率】16.期待値
\(X\)のとる値
\(x_1,x_2,\cdots\cdots,x_n\)
の起こる確率がそれぞれ
\(p_1, p_2,\cdots\cdots,p_n\)
であるとき,
\(X\)の期待値は
\(x_1p_1+ x_2p_2+ x_3p_3+\cdots\cdots+x_np_n\)
【数学A】公式集~図形の性質~
【図形の性質】1.角の二等分線の公式
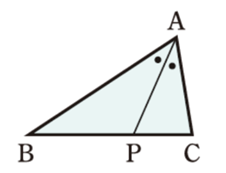
△ABCの\(\angle\)Aの内角の二等分線と辺BCとの交点Pは,辺BCをAB:ACに内分し、次が成り立つ
BP:PC=BA:AC
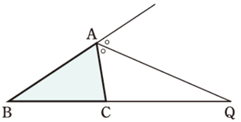
AB \(\ne\)AC である△ABCの\(\angle\)Aの外角の二等分線と辺BCの延長との交点Qは,辺BCをAB:ACに外分し、次が成り立つ
BQ:QC=BA:AC
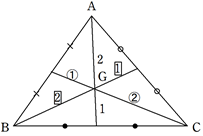
【図形の性質】2.三角形の外心・内心・重心
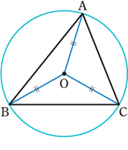
点Oが三角形ABCの外心
①点Oは3辺の垂直二等分線の交点
②点Oは外接円の中心(OA=OB=OC)
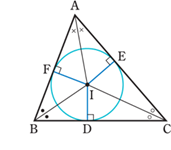
点Iが三角形ABCの内心
①点Iは内角の二等分線の交点
②点Iは内接円の中心(ID=IE=IF)
点Gが三角形ABCの重心
①点Gは3つの中線の交点。
②各頂点から中点までの比が2:1
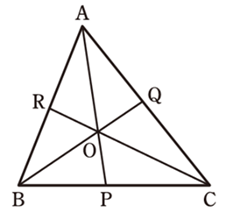
【図形の性質】3.チェバの定理
図において、
\(\frac{RB}{AR} \cdot \frac{PC}{BP} \cdot \frac{QA}{CQ}=1\)
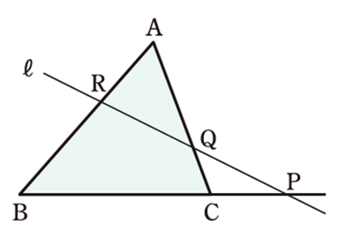
【図形の性質】4.メネラウスの定理
図において、
\(\frac{RB}{AR} \cdot \frac{PC}{BP} \cdot \frac{QA}{CQ}=1\)
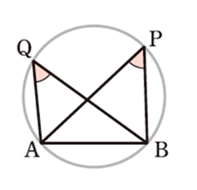
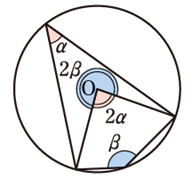
【図形の性質】5.円周角の定理とその逆
① 図において、4点A, B, P, Q が同一円周上にあるとき、
\(\angle\)APB =\(\angle\)AQB
② 円周角は中心角の半分
※特に、直径(中心角\(180^{\circ}\))がつくる円周角は直角(\(90^{\circ}\))
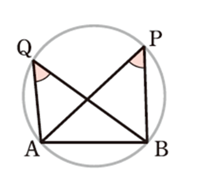
図において、\(\angle\)APB =\(\angle\)AQB が成り立つとき、
4点A, B, P, Q は同一円周上にある
(四角形ABPQは円に内接する)
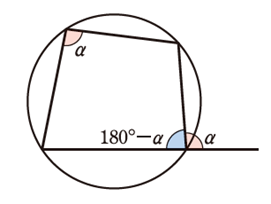
【図形の性質】6.円に内接する四角形
四角形が円に内接するとき、
①対角の和は \(180^{\circ}\)
②内角は,その対角の外角に等しい
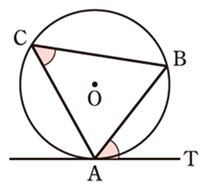
【図形の性質】7.接線と弦の作る角
図において、直線ATが円Oの接線であるとき、
\(\angle ACB = \angle BAT\)
【図形の性質】8.方べきの定理
図において
\(PA \cdot PB =PC \cdot PD\)
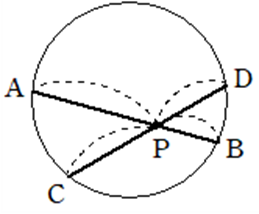
図において
\(PA \cdot PB =PC \cdot PD\)
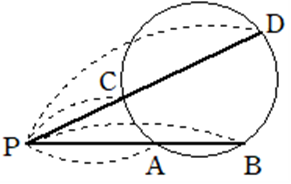
図において
\(PA \cdot PB =PT^2\)
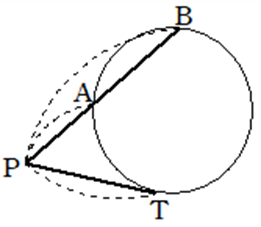
【図形の性質】9.多面体
多角形の面で囲まれた立体を多面体といい、へこみのない多面体を凸多面体という
凸多面体の頂点の数を\(v\), 辺の数を\(e\), 面の数を\(f\)とすると、
\(v-e+f=2\)
が常に成り立つ
【数学A】公式集~数学と人間の活動(整数問題)~
【数学と人間の活動(整数問題)】0.扱う用語一覧
2つの整数 \(a , b\) について,ある整数 \(k\) を用いて, \(a=bk\)と表されるとき,\(b\)は\(a\)の約数,\(a\)は\(b\)の倍数であるという。
素数…\(2\) 以上の自然数で,\(1\) とそれ自身以外に正の約数をもたない数
因数…整数がいくつかの整数の積で表されるとき,積を作る1つ1つの整数
素因数…素数である因数
素因数分解…自然数を素数だけの積の形に表すこと
公約数…\(2\) つ以上の整数に共通な約数
最大公約数…公約数のうち最大のもの
公倍数…2つ以上の整数に共通な倍数
最小公倍数…公倍数のうち正で最小のもの
2つの整数 \(a, b\) の最大公約数が \(1\) であるとき, \(a, b\) は互いに素であるといい、次が成り立つ
\(a, b\) が互いに素で,\(ak\) が \(b\) の倍数であるならば,\(k\) は \(b\) の倍数である
【数学と人間の活動(整数問題)】1.倍数の判定法
\(2\) の倍数 … 一の位が偶数 \((0, 2, 4, 6, 8)\)
\(3\) の倍数 … 各位の数の和が \(3\) の倍数
\(4\) の倍数 … 下 \(2\) 桁が \(4\) の倍数
\(5\) の倍数 … 一の位が \(0\) か \(5\)
\(8\) の倍数 … 下 \(3\) 桁が \(8\) の倍数
\(9\) の倍数 … 各位の数の和が \(9\) の倍数
\(10\) の倍数 … 一の位が \(0\)
\(11\) の倍数 … (偶数桁目の数の和)と(奇数桁目の数の和)の差が \(11\) の倍数
【数学と人間の活動(整数問題)】2.約数の個数
自然数 \(N=p^aq^br^c\cdots\cdots\) と素因数分解できるとき,\(N\) の正の約数の個数は
\((a+1)(b+1)(c+1)\cdots\cdots\)
となる。
例題
\(72\) の正の約数の個数を求めよ。
解答
\(72={2^3} \cdot {3^2}\) より
\(4 \cdot 3 =12\)
より \(12\)個
【数学と人間の活動(整数問題)】3.整数の割り算
整数\(a\)と正の整数\(b\)に対して
\(a = bq + r, 0 \leq r < b\)
を満たす整数 \(q, r\) はただ1通りに定まる。
【数学と人間の活動(整数問題)】4.余りによる整数の分類
余りに着目した整数 \(A\) のおき方
整数 \(A\) は正の整数 \(m\) で割ったときの余りに着目して,次のようにおくことができる
\(mk, mk+1, mk+2, \cdots\cdots, mk + (m-1)\)
例:「ある整数 \(A\) は \(3\) で割ったときの余りが \(2\) である~」
→ \(A = 3k+2 \) (ただし,\(k\) は整数)と表せる
【数学と人間の活動(整数問題)】5.ユークリッドの互除法
2つの自然数 \(a, b\) について,\(a\) を \(b\) で割ったときの商を \(q\) , 余りを \(r\) とすると
\(a\) と \(b\) の最大公約数は,\(b\) と \(r\) の最大公約数に等しい
次の手順で \(a,b\) の最大公約数を求めることができる
STEP① \(a\) を \(b\) で割ったときの余り \(r\) を求める
STEP② \(b\) を \(r\) で割ったときの余り \(s\) を求める
(以下、割る数を余りで割ることを繰り返す)
STEP③ STEP②の結果、余りが \(0\) になったときの割る数が最大公約数となる
【数学と人間の活動(整数問題)】6.\(n\)進法
位取りの基礎を \(n\) として数を表す方法を \(n\) 進法という。また、位取りの基礎となる数 \(n\) を底という。





コメント