【数学Ⅰ】数と式~公式集~
【数と式】1.多項式の乗法
\(m , n \)は正の整数とする。
① \(a^m \times a^n = a^{m+n}\)
② \((a^m)^n = a^{mn}\)
③ \((ab)^n =a^n b^n\)
※\(a^0 =1 \)
①\((a+b)^2 = a^2 + 2ab + b^2\)
\((a-b)^2 = a^2 – 2ab + b^2 \)
②\((a+b) (a-b) = a^2 – b^2 \)
③\((x+a) (x+b) = x^2 + (a+b) x + ab \)
④\((ax+b)(cx+d) = acx^2 + (ad+bc) x + bd\)
\((a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca\)
【数と式】2.因数分解
\(AB + AC = A (B+C) \)
① \(a^2 + 2ab + b^2 = (a+b)^2 , a^2 – 2ab + b^2 = (a-b)^2 \)
② \(a^2 – b^2 = (a+b) (a-b) \)
③ \( x^2 + (a+b) x + ab = (x+a) (x+b)\)
④ \( acx^2 + (ad+bc) x + bd=(ax+b) (cx+d)\) ※たすきがけ
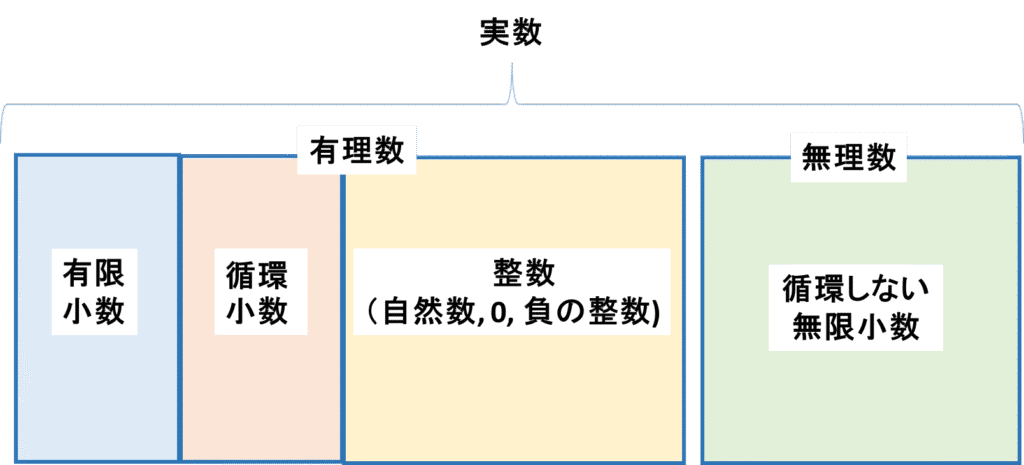
【数と式】3.実数
\( \begin{eqnarray} |x| = \begin{cases} x & (x \geq 0 のとき) \\ -x&(x \lt 0のとき) \end{cases}\end{eqnarray}\)
【数と式】4.平方根
① \(a \geq 0\) のとき \((\sqrt{a})^2 =(- \sqrt{a})^2 = a, \sqrt{a} \geq 0 \)
② \( \begin{eqnarray} \sqrt{a^2}=|a| = \begin{cases} a & (a \geq 0 のとき) \\ -a&(a \lt 0のとき) \end{cases}\end{eqnarray}\)
\(a>0, b>0, k>0 \) のとき
① \(\sqrt{a} \sqrt{b} = \sqrt{ab} \)
② \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \)
③ \(\sqrt{k^2 a} = k \sqrt{a} \)
【数と式】5.1次不等式
① \(A < B \) ならば \(A+C < B+C, A-C < B-C\)
② \(A < B\) ならば
\(C>0\) のとき \(AC < BC, \frac{A}{C} < \frac{B}{C} \)
\(C<0\) のとき \(AC > BC, \frac{A}{C} > \frac{B}{C} \)
STEP① 不等式を \(ax > b, ax \leq b \) などの形に整理する。
STEP② 整理された不等式の両辺を \(x\) の係数 \(a\) で割る。
STEP① それぞれの不等式を解く
STEP② 解いた不等式の共通範囲を求める
【数と式】6.絶対値を含む方程式・不等式
\(c\) が正の定数のとき
① 方程式 \(|x|=c\) の解は \(x=\pm c \)
② 不等式 \(|x|<c\) の解は \(-c<x<c\)
③ 不等式 \(|x|>c\) の解は \(x<-c, c<x \)
【数学Ⅰ】集合と命題~公式集~
【集合と命題】1.集合
\(A, B\) のどちらにも属する要素全体の集合
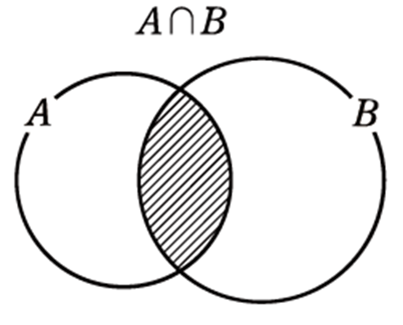
\(A, B\) の少なくとも一方に属する要素全体の集合
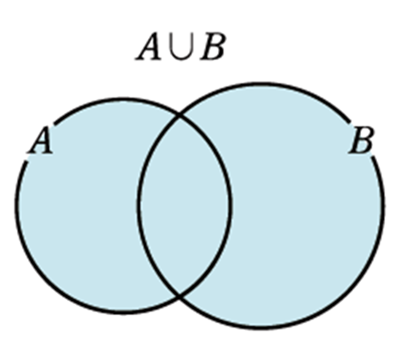
全体集合\(U\)の部分集合\(A\)に対して、\(U\)の要素で,\(A\)には属さない要素全体の集合
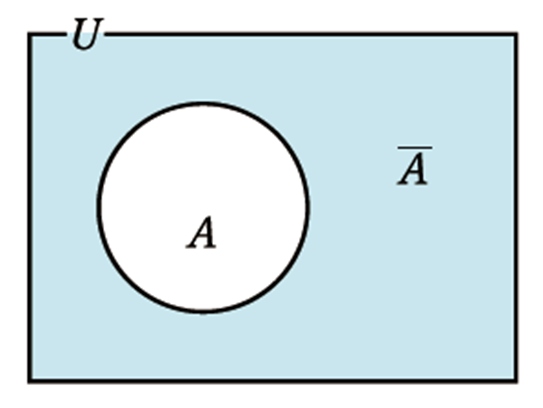
① \(\overline{ A\cap B } =\overline{ A }\cup \overline{ B }\)
② \(\overline{ A\cup B } =\overline{ A }\cap \overline{ B }\)
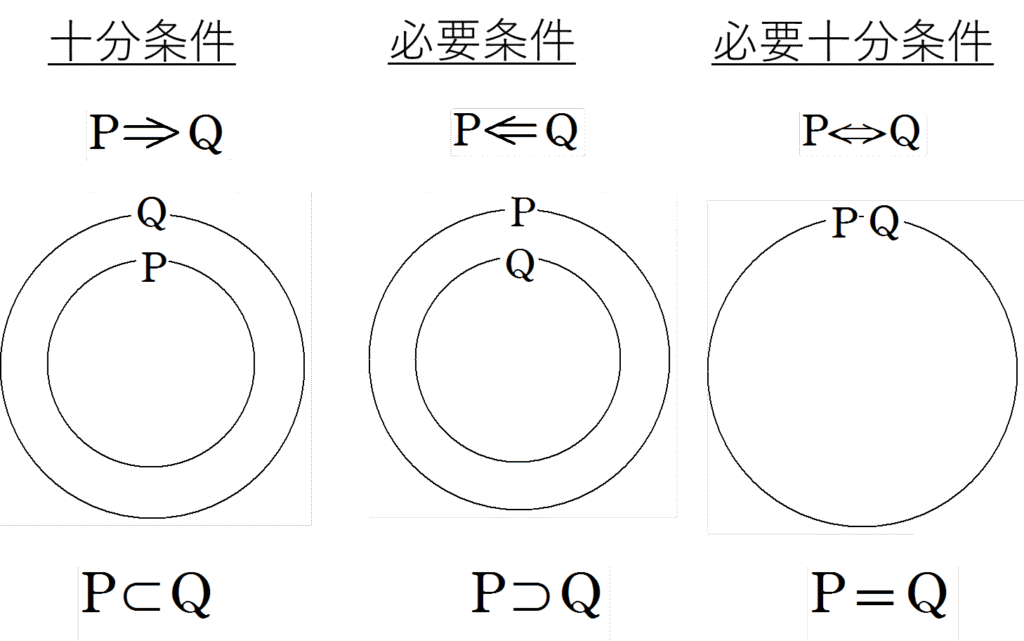
【集合と命題】2.必要条件と十分条件
2つの条件\(p, q\)について
① 命題\(p \Rightarrow q\)が真であるとき
\(p\) は\(q\) であるための 十分条件
\(q\) は\(p\) であるための 必要条件
② 命題\(p \Rightarrow q\)と(q \Rightarrow p\)がともに真であるとき(すなわち、\(p \Leftrightarrow q\)であるとき)
\(p\) は\(q\) (\(q\)は\(p\))であるための 必要十分条件 (\(p\) と\(q\)は同値)
【集合と命題】3.条件の否定
「条件\(p\)でない」という条件を条件\(p\)の否定といい、\(\overline{p}\) で表す。

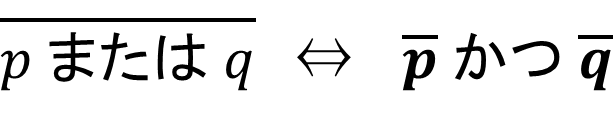
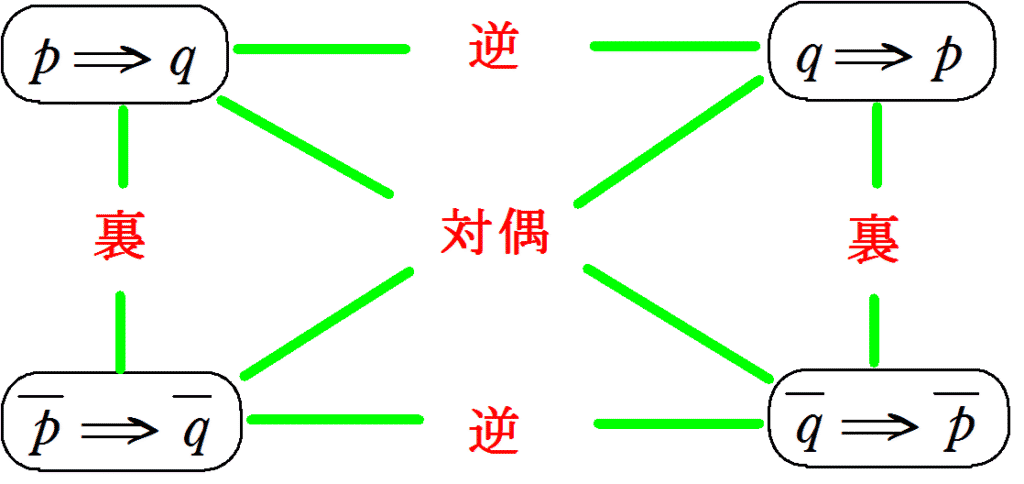
【集合と命題】4.命題の逆・対偶・裏
【集合と命題】5.命題と証明
① 対偶の利用
命題\(p \Rightarrow q\) を証明するには, その対偶\(\overline{q} \Rightarrow \overline{p}\)を証明してもよい。
(命題\(p \Rightarrow q\) とその対偶\(\overline{q} \Rightarrow \overline{p}\)の真偽は一致する)
② 背理法の利用
命題が成り立たないと仮定して矛盾を導く
【数学Ⅰ】2次関数~公式集~
【2次関数】1.2次関数のグラフ
頂点:点\((p, q)\)
軸:直線\(x=p\)
※\(y=ax^2\) のグラフを
\(x\)軸方向に\(p\)
\(y\)軸方向に\(q\)
だけ平行移動した放物線を表す。
\(ax^2+bx+c\)の形を\(a(x-p)^2+q\)に変形することを平方完成という。
\(x^2-2px=(x-p)^2-p^2\)
平方完成すると
\(y=a(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a}\)に変形できる。
頂点:\((-\frac{b}{2a}, -\frac{b^2-4ac}{4a})\)
軸:直線 \(x=-\frac{b}{2a}\)
【2次関数】2.平行移動
\(x\)方向に\(p\), \(y\)軸方向に\(q\)平行移動
①点\((a, b)\) → \((a+p, b+p)\)
②関数\(y=f(x)\)
→ \(y-q=f(x-p)\) すなわち \(y=f(x-p)+q\)
※関数の平行移動は
\(x\) → \(x-p\)
\(y\) → \(y-q\)
に置き換えればOK
【2次関数】3.対称移動
①点\((a, b)\)
\(x\)軸対称 → \((a, -b)\)
\(y\)軸対称 → \((-a, b)\)
原点対称 → \((-a, -b)\)
②関数\(y=f(x)\)
\(x\)軸対称 → \(-y=f(x)\) ⇔\(y=-f(x)\)
\(y\)軸対称 → \(y=f(-x)\)
原点対称 → \(-y=f(-x)\) ⇔\(y=-f(-x)\)
※\(x\)軸対称は\(y\),
\(y\)軸対称は\(x\),
原点対称は\(x, y\)両方
の符号が変わると覚える
【2次関数】4.2次関数の最大値・最小値
STEP① 平方完成して、\(y=a(x-p)^2+q\)の形にする。
STEP② 頂点・軸を求め、グラフをかく
STEP③ グラフの\(y\)座標が最も大きい値(最大値)、最も小さい値(最小値)を求める
【2次関数】5.2次関数の決定
STEP① 求める2次関数をおく
①放物線の頂点・軸・最大値・最小値関係がわかっている場合
→ \(y=a(x-p)^2+q\)とおく
②グラフが通る3点がわかっている場合
→ \(y=ax^2+bx+c\)とおく
③\(x\)軸との交点がわかっている場合
→ \(y=a(x-α)(x-β)\) とおく
STEP② STEP①でおいた2次関数に条件をあてはめて立式する
STEP③ 立式した方程式を解き、条件を満たす2次関数を求める。
【2次関数】6.2次方程式
2次方程式\(ax^2+bx+c=0\)の解は
\(x=\frac{-b±\sqrt{b^2-4ac}}{2a}\)
2次方程式\(ax^2+2b’x+c=0\)(\(x\)の項が偶数の場合)の解は
\(x=\frac{-b’±\sqrt{b’^2-ac}}{a}\)
①因数分解の利用
⇒ 左辺が因数分解できるとき
②平方根の利用
⇒ \(x^2=p\)の形になるとき(\(x\)の項がないとき)
③解の公式の利用
⇒ ①,②以外のとき
2次方程式 \(ax^2+bx+c=0\)の判別式\(D=b^2-4ac\)において
\(D>0\) ⇔ 異なる2つの実数解をもつ(解は2個)
\(D=0\) ⇔ 重解をもつ(解は1個)
\(D<0\) ⇔ 実数解をもたない(解は0個)
※特に、\(D \geq 0\) ⇔ 実数解をもつ(解は1個or2個)
2次方程式 \(ax^2+2b’x+c=0\)の判別式\(D/4={b’}^2-ac\)において
\(D/4>0\) ⇔ 異なる2つの実数解をもつ(解は2個)
\(D/4=0\) ⇔ 重解をもつ(解は1個)
\(D/4<0\) ⇔ 実数解をもたない(解は0個) ※特に、\(D/4 \geq 0\) ⇔ 実数解をもつ
【2次関数】7.2次関数のグラフと\(x\)軸の交点の個数
2次関数\(y=ax^2+bx+c\) のグラフと\(x\)軸の交点の数は\(D=b^2-4ac\)において
\(D>0\) ⇔ 異なる2点で交わる(交点は2個)
\(D=0\) ⇔ 1点で接する(交点は1個)
\(D<0\) ⇔ 共有点をもたない(交点は0個)
※特に、\(D \geq 0\) ⇔ 交点をもつ(交点は1個or 2個)
【2次関数】8.2次不等式の解
STEP① 2次方程式\(ax^2+bx+c=0\)を解き、2次関数\(y=ax^2+bx+c\) と\(x\)軸との交点を求める。
STEP② \(x\)軸との交点を利用して2次関数\(y=ax^2+bx+c\)のグラフをかく
STEP③ グラフから条件を満たす\(x\)の範囲を求める
【数学Ⅰ】図形と計量(三角比)~公式集~
【図形と計量】1.三角比の定義
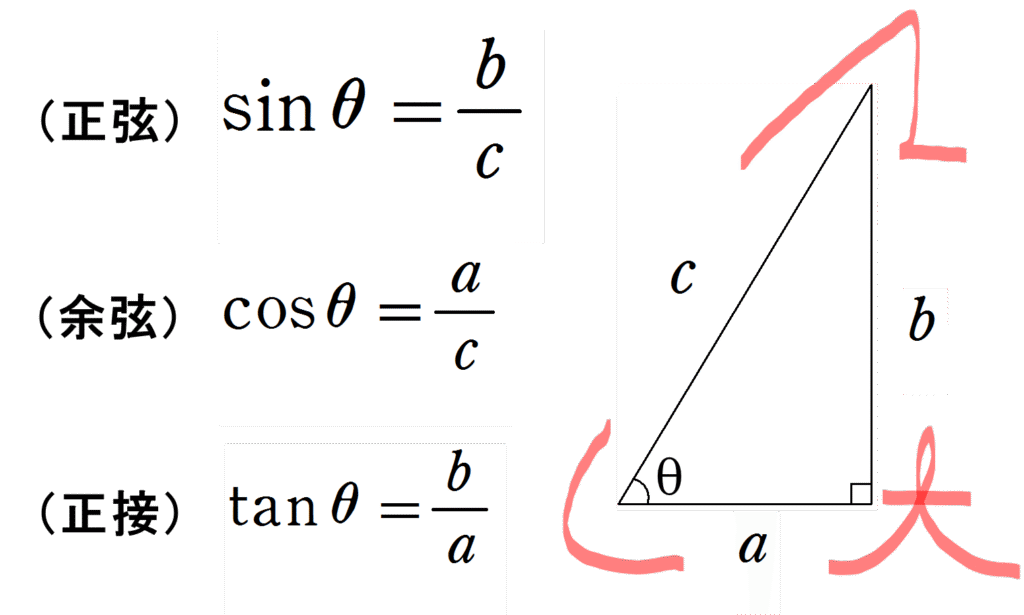
すなわち、

【図形と計量】2.三角比の値
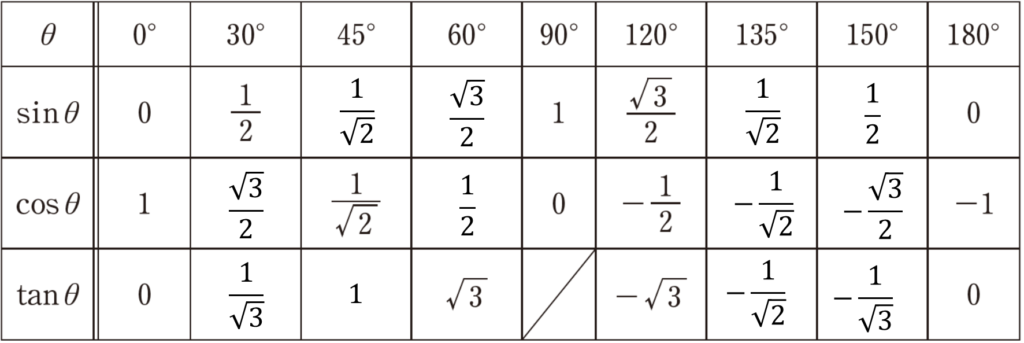
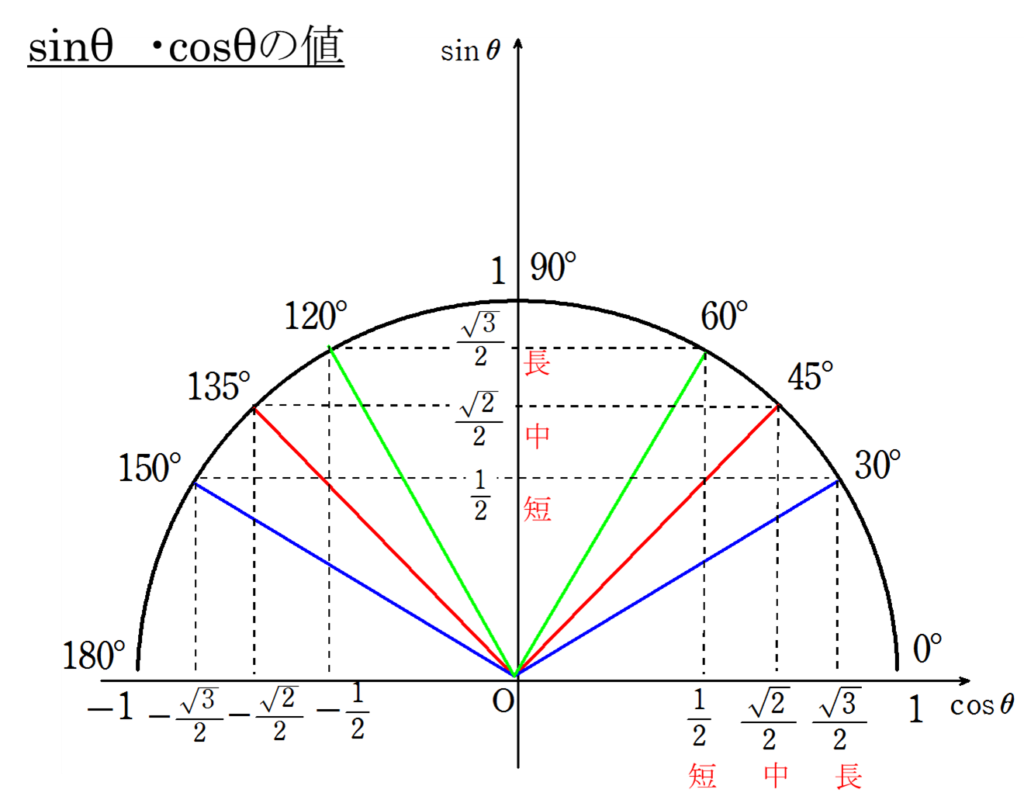
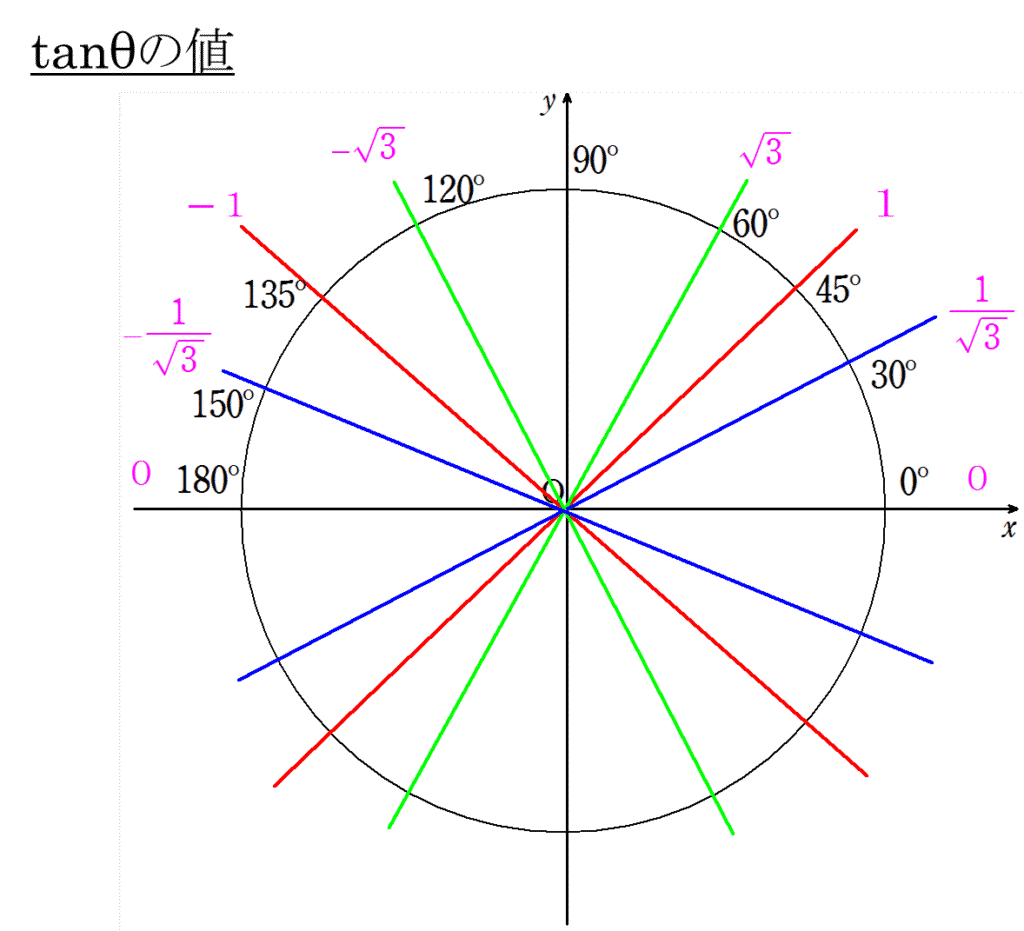
【図形と計量】3.90°ーθ,180°ーθの三角比
①\(\sin{(90°-\theta)}=\cos\theta\)
②\(\cos{(90°-\theta)}=\sin\theta\)
③\(\tan{(90°-\theta)}=\frac{1}{\tan\theta}\)
\(\sin{(180°-\theta)}=\sin\theta\)
\(\cos{(180°-\theta)}=-\cos\theta\)
\(\tan{(180°-\theta)}=-\tan\theta\)
【図形と計量】4.三角比の符号
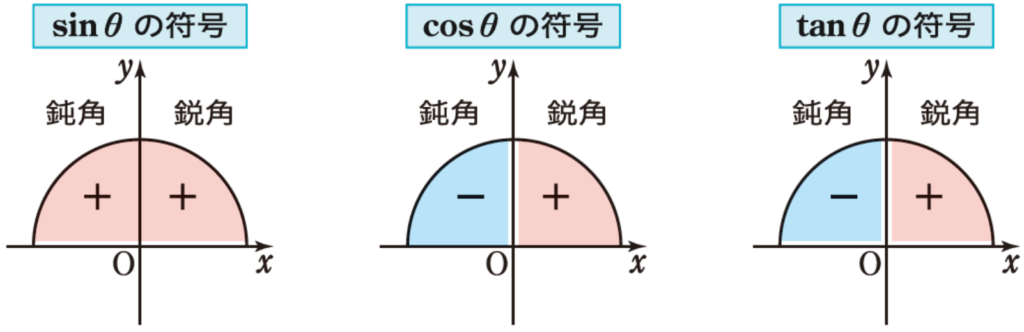
【図形と計量】5.三角比の相互関係
①\(tan\theta = \frac{sin\theta}{cos\theta}\)
②\(sin^2 \theta +cos^2 \theta =1 \)
③\(1+tan^2 \theta =\frac{1}{cos^2 \theta}\)
【図形と計量】6.正弦定理
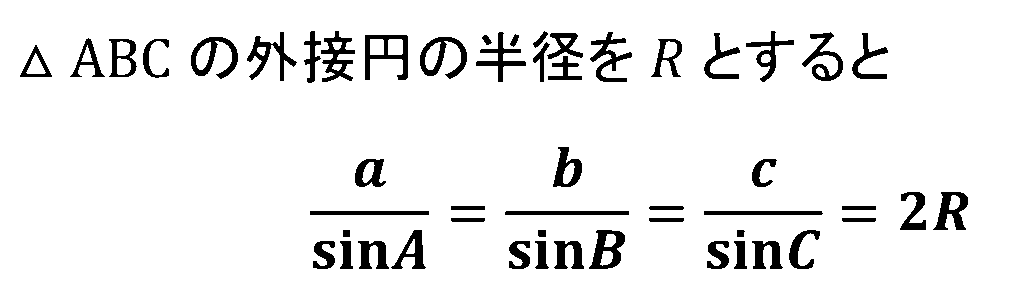
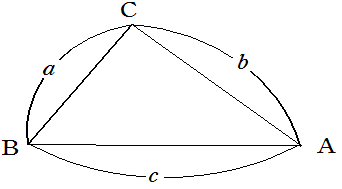
【図形と計量】7.余弦定理
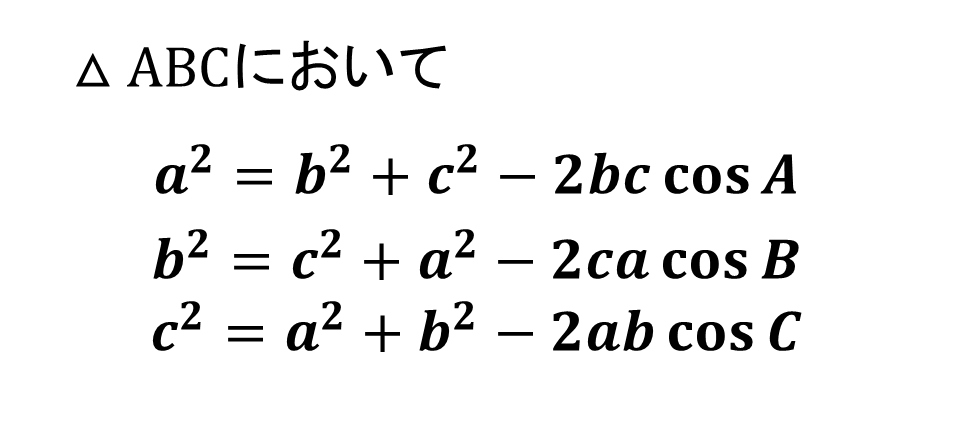

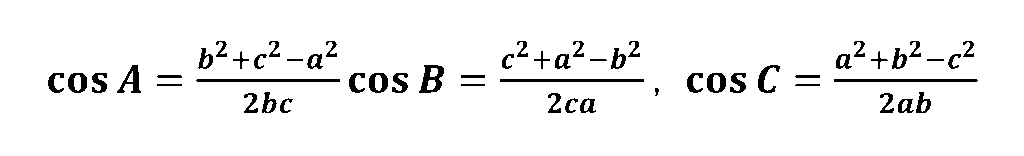
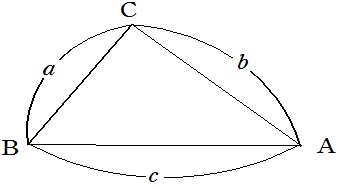
【図形と計量】8.三角形の面積
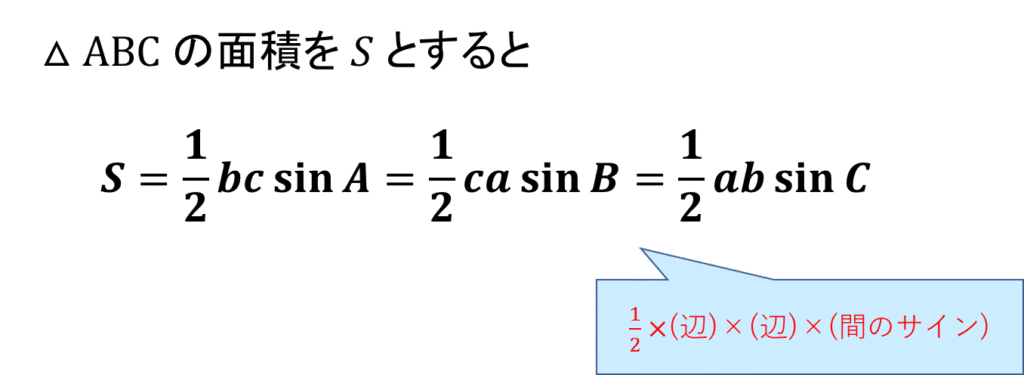

【数学Ⅰ】データの整理~公式集~
【データの分析】1.データの整理
データのとる値をいくつかの区間に区切って階級を定め、各階級に度数を対応させた表。
各階級の真ん中の値を階級値という。
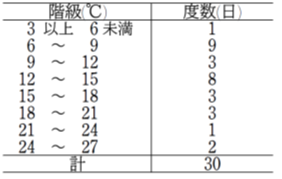
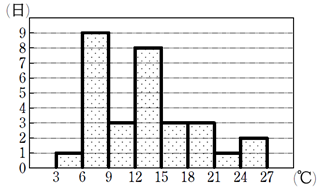
度数分布表を柱状のグラフで表したもの
【データの分析】2.データの代表値
\(\overline{x}=\displaystyle\frac{1}{n}(x_1+x_2+ \cdots\cdots +x_n)\)
例題
次のデータの平均値を求めよ。
\(8, 5, 5,6, 7\)
解答
平均値\(\overline{x}=\displaystyle\frac{1}{5}(8+5+5+6+7)\)
\(=6.2\)
データにおける最も個数の多い値。
度数分布表における度数が最も大きい階級の階級値
例題
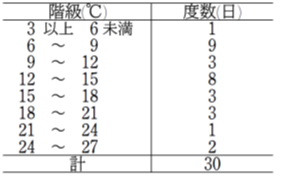
次のデータの最頻値を求めよ。
解答
度数分布表において、度数が最も大きい階級は「\(6 \sim 9\)」であるからその階級値\(7.5\)が最頻値となる。
データを値の大きさの順に並べたとき中央の位置にくる値。
データの大きさが偶数のときは,中央に並ぶ2つの値の平均値。
例題
次のデータの中央値を求めよ。
①\(3, 7, 8, 9, 5\)
②\(2, 7, 9, 6, 2, 5\)
解答
①データを並び替えると
\(3, 5, 7, 8, 9\)
より、中央値は 7
②データを並び替えると
\(2, 2, 5, 6, 7, 9\)
より、中央値は \(\displaystyle\frac{5+6}{2}=5.5\)
【データの分析】3.四分位数
データの最大値から最小値を引いた差の値
例題
ある都市のA市における月ごとの降水日数
\(7, 4, 9, 7, 10, 13, 14, 7, 4, 12, 13, 5\)
のデータの範囲を求めよ。
解答
\(14-4=10\)(日)
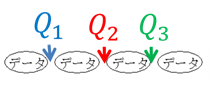
四分位数:データの値を大きさの順に並べたとき,4等分する位置にくる値。
小さい方から順に,第1四分位数\(Q_1\),第2四分位数\(Q_2\),第3四分位数\(Q_3\)という。
※(第2四分位数\(Q_2\))=(中央値)
四分位範囲:第3四分位数\(Q_3\)と第1四分位数\(Q_1\)の差\(Q_3-Q_1)\)
四分位偏差:四分位範囲の半分\(\displaystyle\frac{ Q_3-Q_1}{2}\)
例題
データ\(21, 38, 41, 52, 58, 60\)における
第1四分位数\(Q_1\),
第2四分位数\(Q_2\),
第3四分位数\(Q_3\),
四分位範囲
四分位偏差
を求めよ。
解答
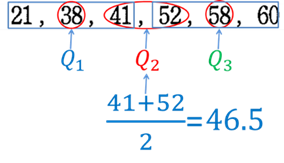
第1四分位数\(Q_1\):\(38\)
第2四分位数\(Q_2\):\(46.5\)
第3四分位数\(Q_3\):\(58\)
四分位範囲:\(58-38=20\)
四分位偏差:\(\displaystyle\frac{20}{2}=10\)
【データの分析】4.箱ひげ図
箱ひげ図:データの最小値,第1四分位数,中央値第3四分位数,最大値を,箱とひげ(線)で表した図。
外れ値:データの中で,他の値から極端に離れた値。
例題
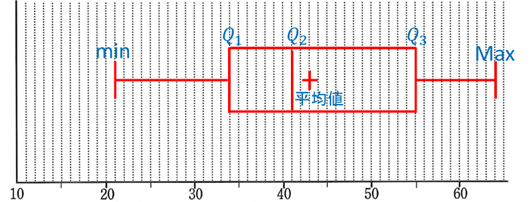
次のデータの最大値,最小値,平均値,四分位数を求め, 箱ひげ図をかけ。
\(21, 32, 36, 38, 41, 45, 52, 58, 64\)
解答
最小値:\(21\)
最大値:\(64\)
平均値:\(43\)
中央値\(Q_2\):\(41\)
第1四分位数\(Q_1\):\(34\)
第3四分位数:\(Q_3\):\(55\)
【データの分析】5.分散と標準偏差
偏差:変量\(x\)の各値と平均値との差
\(x_1-\overline{x}, x_2-\overline{x}, \cdots\cdots , x_n-\overline{x}\)
分散\(s^2\):偏差の2乗の平均値
\(s^2=\displaystyle\frac{1}{n}\{(x_1-\overline{x})^2+(x_2-\overline{x})^2+\cdots\cdots\)\(+(x_n-\overline{x})^2\}\)
\(s^2=\overline{x^2}-(\overline{x})^2\)
標準偏差\(s\):分散\(s^2\)の正の平方根
標準偏差\(s=\sqrt{s^2}\)
例題
データ\(5, 2, 8, 4, 6\)における分散\(s^2\),標準偏差\(s\)を求めよ。
解答
平均値\(\overline{x}=\displaystyle\frac{1}{5}(5+2+8+4+6)=5\)
より
分散\(s^2=\displaystyle\frac{1}{5}((5-5)^2+(2-5)^2\)\(+(8-5)^2+(4-5)^2+(6-5)^2\)
\(=4\)
標準偏差\(s=\sqrt{4}=2\)
※\(x^2\)のデータの平均値\(\overline{x^2}\)
\(=\displaystyle\frac{1}{5}(5^2+2^2+8^2+4^2+6^2)\)
\(=29\)
よって
分散\(s^2=29-5^2=4\)でも可
【データの分析】6.相関関係
散布図:2つの変量からなるデータを平面上に図示した図
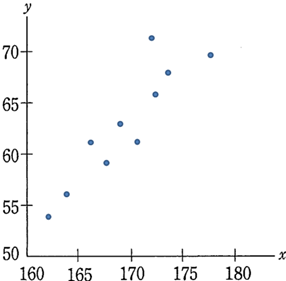
2つの変量からなるデータにおいて
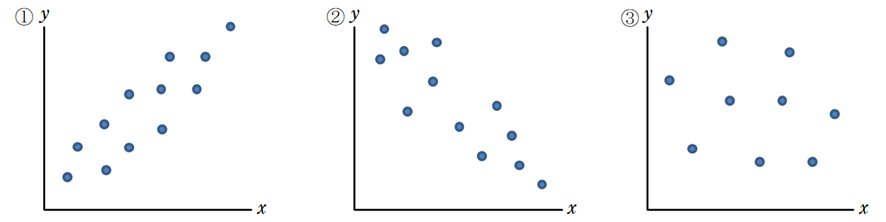
① 一方が増加すると他方も増加する傾向がある → 正の相関
② 一方が増加すると他方が減少する傾向がある → 負の相関
③ ①②のどちらでもない → 相関がない
【データの分析】7.相関係数
2つの変量\(x, y\)において,\(x\)の偏差と\(y\)の偏差の積\((x_k-\overline{x})(y_k-\overline{y})\)
\(s_{xy}=\displaystyle\frac{1}{n}\{(x_1-\overline{x})(y_1-\overline{y})+\)\((x_2-\overline{x})(y_2-\overline{y})+\)\(\cdots\cdots+(x_n-\overline{x})(y_n-\overline{y})\}\)
例題
次の表は,ある地域における,午前10時から午後3時までの気温\(x\)と湿度\(y\)を1時間ごとに観測した結果である。
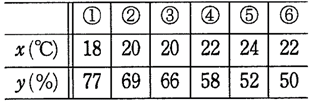
このとき,\(x,y\)の共分散\(s_{xy}\)を求めよ。
解答
\(\overline{x}=\displaystyle\frac{1}{6}(18+20+20+22+24\)\(+22)\)
\(=21\)
\(\overline{y}=\displaystyle\frac{1}{6}(77+69+66+58+52\)\(+50)\)
\(=62\)
共分散\(s_{xy}=\frac{1}{6}\{(18-21)(77-62)\)\(+(20-21)(69-62)\)\(+(20-21)(66-62)\)\(+ (22-21)(58-62)\)\(+ (24-21)(52-62)\)\(+ (22-21)(50-62)\}\)
\(=-17\)
\(x\)と\(y\)の共分散\(s_{xy}\)を,\(x\)の標準偏差\(s_x\)と\(y\)の標準偏差\(s_y\)の積で割った値
相関係数\(r=\displaystyle\frac{s_{xy}}{s_xs_y}\)
\(=\displaystyle\frac{(xとyの共分散)}{(xの標準偏差)×(yの標準偏差)}\)
※\(-1 \leq r \leq 1\)
正の相関が強い:相関係数\(r\)が\(1\)に近い値となる
負の相関が強い:相関係数\(r\)が\(-1\)に近い値となる
相関がない:相関係数\(r\)が\(0\)に近い値となる
例題
次のデータ\(x,y\)における相関係数を求めよ。
また、これらの間にはどのような相関関係があると考えられるか。
\(x\)の平均値:\(6\)
\(y\)の平均値:\(4\)
\(x\)と\(y\)の共分散:\(-4\)
\(x\)の分散:\(9.6\)
\(y\)の分散:\(2.4\)
解答
相関係数\(r=\displaystyle\frac{-4}{\sqrt{9.6 \times 2.4 }}\)
\(=-0.833 \cdots\)
よって、負の相関がある
【データの分析】8.仮説検定
得られたデータをもとに,ある主張が正しいかどうかを仮説を立てて判断する手法








コメント