１．集合
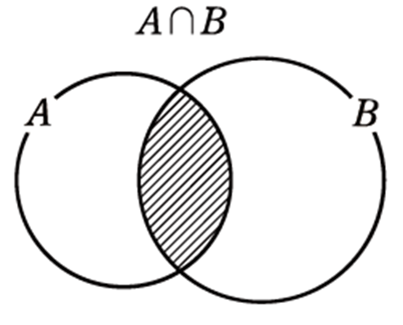
\(A, B\) のどちらにも属する要素全体の集合
例題
\(A=\{1, 2, 5, 7\}, B=\{0, 1, 5, 8\} \)において，\(A \cap B\) を求めよ。
解答
\(A \cap B=\{1, 5\}\)
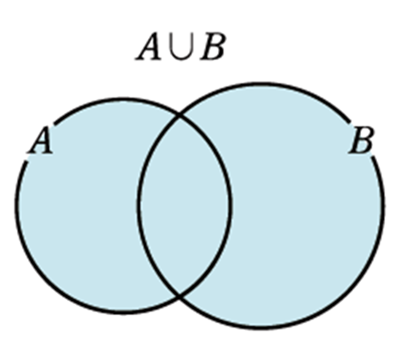
\(A, B\) の少なくとも一方に属する要素全体の集合
例題
\(A=\{1, 2, 5, 7\}, B=\{0, 1, 5, 8\} \)において，\(A \cup B\) を求めよ。
解答
\(A \cup B=\{0,1,2,5,7,8\}\)
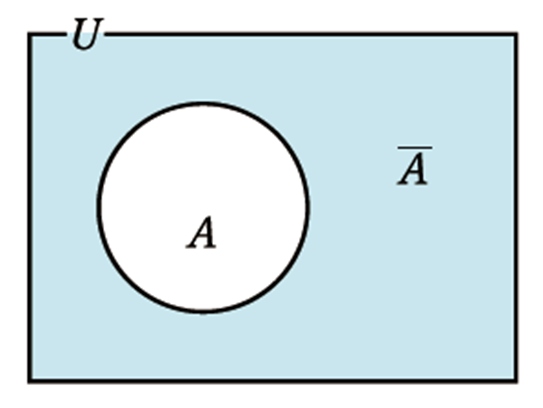
全体集合\(U\)の部分集合\(A\)に対して、\(U\)の要素で，\(A\)には属さない要素全体の集合
例題
\(U=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}\)を全体集合とするとき，
\(U\)の部分集合\(A=\{1,2,3,5,7,9\}\)において補集合\(\overline{A}\)を求めよ。
解答
\(\overline{A}=\{4,6,8\}\)
① \(\overline{ A\cap B } =\overline{ A }\cup \overline{ B }\)
② \(\overline{ A\cup B } =\overline{ A }\cap \overline{ B }\)
例題
\(U=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}\)を全体集合とする。\(U\)の部分集合\(A\),\(B\)について
\(A \cup B=\{1,2,5,7,8\}\)であるとき, 集合\(\overline{A}\cap \overline{B}\)を求めよ。
解答
\(\overline{A}\cap \overline{B}=\overline{A \cup B}=\{3,4,6,9\}\)
２．必要条件と十分条件
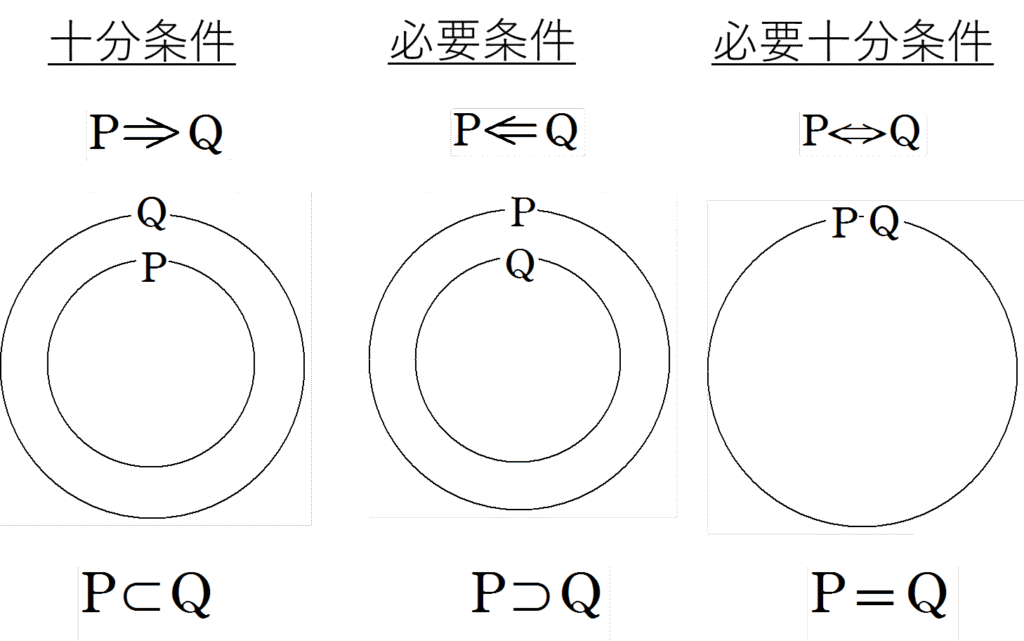
２つの条件\(p, q\)について
① 命題\(p \Rightarrow q\)が真であるとき
\(p\) は\(q\) であるための 十分条件
\(q\) は\(p\) であるための 必要条件
② 命題\(p \Rightarrow q\)と(q \Rightarrow p\)がともに真であるとき（すなわち、\(p \Leftrightarrow q\)であるとき)
\(p\) は\(q\) (\(q\)は\(p\))であるための 必要十分条件 (\(p\) と\(q\)は同値）
例題
\(x\)は実数とする。
次の□の中は，
「必要条件であるが十分条件でない」，「十分条件であるが必要条件ではない」，「必要十分条件である」，「必要条件でも十分条件でもない」
のうちそれぞれどれが適するか。
① \(x=2\) は\(x^2-5x+6=0\) であるための □。
② \(x=1,2,3\) は \((x-1)(x-2)=0\)であるための □。
③ \(|x|=0\) は \(x=0\) であるための □。
解答
① \(x^2-5x+6=0\)の解は\(x=2, 3\) より
\(x=2 \Rightarrow x^2-5x+6=0 \) は 真
\(x^2-5x+6=0 \Rightarrow x=2 \) は 偽
であるから 「十分条件であるが必要条件ではない」
② \((x-1)(x-2)=0\)の解は\(x=1, 2\)より
\(x=1, 2, 3 \Rightarrow (x-1)(x-2)=0 \) は 偽
\((x-1)(x-2)=0 \Rightarrow x=1, 2, 3 \) は 真
であるから 「必要条件であるが十分条件ではない」
③\(|x|=0\)の解は\(x=0\)より
\(|x|=0 \Rightarrow x=0\) は真
\(x=0 \Rightarrow |x|=0\) は真
であるから 「必要十分条件である」
３．条件の否定
「条件\(p\)でない」という条件を条件\(p\)の否定といい、\(\overline{p}\) で表す。
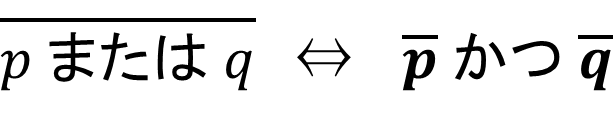
例題
次の条件の否定を求めよ。
\(x<7 または x=2\)
解答
与えられた条件の否定は
\(\overline{x<7} かつ \overline{x=2}\)
より
\(x \geq 7 かつ x \neq 2\)
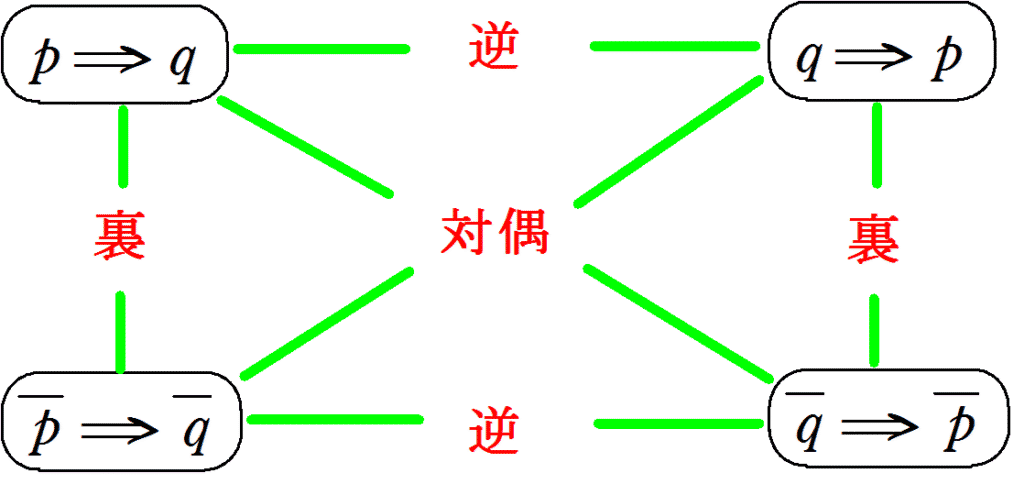
４．命題の逆・対偶・裏
例題
\(n\)を自然数とするとき，次の命題の真偽を調べよ。
また，その逆，対偶，裏を述べ，それらの真偽を調べよ。
\(n\)は\(4\)の倍数である\(\Rightarrow\) \(n\) は\(2\) の倍数である
解答
\(n\)が4の倍数であるとき、必ず2の倍数になるため、命題は真である
また、この命題の逆，対偶，裏は以下のようになる
逆：\(n\)は\(2\)の倍数である\(\Rightarrow\) \(n\) は\(4\) の倍数である 偽（反例：\(n=6\))
対偶：\(n\)は\(2\)の倍数でない\(\Rightarrow\) \(n\) は\(4\) の倍数でない 真
裏：\(n\)は\(4\)の倍数でない\(\Rightarrow\) \(n\) は\(2\) の倍数でない 偽（反例:\(n=6\))
５．命題と証明
① 対偶の利用
命題\(p \Rightarrow q\) を証明するには, その対偶\(\overline{q} \Rightarrow \overline{p}\)を証明してもよい。
（命題\(p \Rightarrow q\) とその対偶\(\overline{q} \Rightarrow \overline{p}\)の真偽は一致する）
② 背理法の利用
命題が成り立たないと仮定して矛盾を導く
例題
① \(n\)は整数とする。\(n^2\)が\(3\)の倍数でないならば，\(n\)は\(3\)の倍数でないことを証明せよ。
②\(\sqrt{2}\)が無理数であることを用いて，\(1+\sqrt{3}\)が無理数であることを証明せよ。
解答
① 対偶：「\(n\)が3の倍数ならば，\(n^2\)は3の倍数である」
ことを示せばよい。
\(n\)が\(3\)の倍数のとき，\(n=3k\)(\(k\)は整数)とすると，
\(n^2=(3k)^2=9k^2\)
より，3の倍数であるから，成り立つ。
よって、対偶が成り立つから元の命題も成り立つ。
② \(1+\sqrt{2}\)は有理数であると仮定すると
\(1+\sqrt{2}=r\)\((rは有理数)\)と表せる。
このとき，
\(\sqrt{2}=r-1\)であるが，\(r-1\)は有理数であるから， \(\sqrt{2}\)が無理数であることと矛盾する。
したがって，\(1+\sqrt{2}\)は無理数である
コメント