ここでは、【数学II】でよく利用する公式(基礎知識)を一覧にしてまとめています。
【数学II】式と証明~公式集一覧~
【式と証明】1.3次式の展開と因数分解
①\((a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3\)
②\((a – b)^3 = a^3 – 3a^2b + 3ab^2 – b^3\)
①\(a^3 + b^3 = (a + b)(a^2 – ab + b^2)\)
②\(a^3 – b^3 = (a – b)(a^2 + ab + b^2)\)
【式と証明】2.二項定理
\((a + b)^n\)
\(= {}_nC_n a^n + {}_nC_{n-1} a^{n -1}b + {}_nC_{n-2} a^{n -2}b^2\)
\(+ \cdots + {}_nC_{r} a^rb^{n-r} + \cdots + {}_nC_{0} b^n\)
【式と証明】3.多項式の割り算
\(A\) を \(B\)で割ったときの商を\(Q\), 余りを\(R\)とするとき
\(A = BQ + R\)
と表せる。
※(割られる式)=(割る式)×(商)+(余り)
【式と証明】4.分数式
①\(\displaystyle\frac{A}{B} \times \displaystyle\frac{C}{D}=\displaystyle\frac{AC}{BD}\)
②\(\displaystyle\frac{A}{B} \div \displaystyle\frac{C}{D}\)\(=\displaystyle\frac{A}{B}\times\displaystyle\frac{D}{C}\)\(=\displaystyle\frac{AD}{BC}\)
③\(\displaystyle\frac{A}{C} + \displaystyle\frac{B}{C}=\displaystyle\frac{A+B}{C}\)
④\(\displaystyle\frac{A}{C} – \displaystyle\frac{B}{C}=\displaystyle\frac{A-B}{C}\)
【式と証明】5.恒等式の性質
① \(ax^2 + bx + c = a’x^2 + b’x + c’\) が\(x\) の恒等式
⇔ \(a = a’, b = b’, c = c’\)
② \(ax^2 + bx + c = 0\) が \(x\) の恒等式
⇔ \(a = b = c = 0\)
【式と証明】6.等式・不等式の証明
①(左辺)or(右辺)を変形して,他方になることを示す
②(左辺)-(右辺)を変形して,\((左辺) – (右辺) = 0\) を示す
①(左辺)―(右辺)\(\geq 0\) を示す
②\((左辺)^2 –(右辺)^2 \geq 0\) を示す
実数\(a, b\) について
①\(a^2 \geq 0\) (等号成立は\(a = 0\) のとき成り立つ)
②\(a^2 + b^2 \geq 0\) (等号成立は\(a = b = 0\) のとき成り立つ)
\(a > 0, b > 0\) のとき
\(\displaystyle\frac{a + b}{2} \geq \sqrt{ab}\)
(等号成立は \(a = b\) のとき成り立つ)
【数学II】複素数と方程式~公式集一覧~
【複素数と方程式】1.複素数の性質
\(a, b, c, d\) は実数とする。
\(i^2 = -1\)を満たす数を\(i\)と表す。
※特に、\(a > 0\) において \(\sqrt{- a} = \sqrt{a} i \)
複素数 \(a +bi\)において
①\(a\) : 実部 , \(b\) : 虚部 という
②実数のとき, \(b = 0\)
③虚数のとき, \(b \neq 0\)
④純虚数のとき, \(a = 0, b \neq 0\)
\(a + bi = c +di ⇔ a = c かつ b = d\)
特に、\(a + bi = 0 ⇔ a = 0 かつ b = 0\)
【複素数と方程式】2.2次方程式の解の種類の判別
\(ax^2 + bx + c = 0 (a \neq 0)\) の判別式 \(D = b^2 – 4ac\) において
①\(D > 0\) ⇔ 異なる2つの実数解をもつ(実数解2個)
②\(D = 0\) ⇔ 重解をもつ(実数解1個)
③\(D < 0\) ⇔ 異なる2つの虚数解をもつ(実数解なし)
※\(D \geq 0\) ⇔ 実数解をもつ(実数解1or2個)
【複素数と方程式】3.解と係数の関係
2次方程式\(ax^2 + bx + c = 0 (a \neq 0)\) の2つの解を\(\alpha, \beta\) とするとき
和:\(\alpha + \beta = -\displaystyle\frac{b}{a}\)
積:\(\alpha\beta = \displaystyle\frac{c}{a}\)
\(ax^2 + bx + c = 0 (a \neq 0)\) の2つの解を\(\alpha, \beta\) とするとき
\(ax^2 + bx + c = a(x – \alpha)(x – \beta)\)
2数\(\alpha, \beta\) を解とする2次方程式の1つは
①\((x – \alpha)(x – \beta) = 0\)
②\(x^2 –(\alpha + \beta)x +\alpha\beta = 0\)
【複素数と方程式】4.剰余の定理
\(P(x)\) を\((x – k)\)で割った商を \(Q(x)\)、余りを\(R\)とすると
①\(P(x) = (x – k)Q(x) + R\) と表せる
② \(P(k) = R\)
【複素数と方程式】5.因数定理
多項式\(P(k) = 0\) ⇔ 多項式\(P(x)\) は \((x – k)\) を因数にもつ
【数学II】図形と方程式~公式集一覧~
【図形と方程式】1.点の座標
2点\(A(x_1, y_1), B(x_2, y_2)\)の距離ABは
AB = \(\sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}\)
2点\(A(x_1, y_1), B(x_2, y_2)\)を結ぶ線分ABについて
①\(m : n\) に内分する点は
\(\left(\displaystyle\frac{nx_1 + mx_2}{m + n}, \displaystyle\frac{ny_1 + my_2}{m + n}\right)\)
②\(m : n\) に外分する点は
\(\left(\displaystyle\frac{-nx_1 + mx_2}{m – n}, \displaystyle\frac{-ny_1 + my_2}{m – n}\right)\)
③中点は
\(\left(\displaystyle\frac{x_1 + x_2}{2},\displaystyle\frac{y_1 + y_2}{2}\right)\)
3点\(A(x_1, y_1), B(x_2, y_2), C(x_3, y_3)\) を頂点とする△ABCの重心は
\(\left(\displaystyle\frac{x_1 + x_2 + x_3 }{3},\displaystyle\frac{y_1 + y_2 + y_3}{3}\right)\)
【図形と方程式】2.直線の方程式
①点\((x_1, y_1)\) を通り,傾きが \(m\) の直線の方程式は
\(y – y_1 = m(x – x_1)\)
②点\((x_1, y_1)\) を通り,\(x\) 軸に垂直な直線の方程式は
\(x = x_1\)
2点\((x_1, y_1), (x_2, y_2)\)を通る直線の方程式は
①\(x_1 \neq x_2\) のとき
\(y – y_1 = \displaystyle\frac{y_2 – y_1}{x_2 – x_1}(x – x_1)\)
②\(x_1 = x_2\) のとき
\(x = x_1\)
【図形と方程式】3.2直線の平行・垂直
2直線\(y = m_1 x + n_1 , y = m_2 x + n_2\) について
①平行 ⇔ \(m_1 = m_2\)
②垂直 ⇔ \(m_1m_2 = -1\) ⇔ \(m_1 = -\displaystyle\frac{1}{m_2}\)
【図形と方程式】4.点と直線の距離
点\((x_1, y_1)\) と直線 \(ax + by + c = 0\) の距離\(d\) は
\(d = \displaystyle\frac{|ax_1 + by_1 + c|}{\sqrt{a^2 + b^2}}\)
※特に、原点\((0, 0)\) と直線 \(ax + by + c = 0\) の距離\(d\) は
\(d = \displaystyle\frac{|c|}{\sqrt{a^2 + b^2}}\)
【図形と方程式】5.円の方程式
中心\((a, b)\), 半径\(r\) の円の方程式は
\((x – a)^2 + (y – b)^2 = r^2\)
※特に、原点中心、半径\(r\) の円の方程式は
\(x^2 + y^2 = r^2\)
①中心と半径がわかる場合など
⇒ \((x – a)^2 + (y – b)^2 = r^2\)
②通る点がわかる場合など
⇒ \(x^2 + y^2 + lx +my + n = 0\)
【図形と方程式】6.円と直線の方程式
円の半径を\(r\) , 円の中心から直線までの距離を\(d\)とするとき
①円と直線が異なる2点で交わる ⇔ \(d < r\)
②円と直線が接する ⇔ \(d = r\)
③円と直線が交わらない ⇔ \(d > r\)
円 \(x^2 + y^2 = r^2\) 上の点\((x_1, y_2)\) における接線の方程式は
\(x_1 x + y_1 y = r^2\)
【図形と方程式】7.2つの円の位置関係
2つの円\(C_1\), \(C_2\) の半径をそれぞれ\(r , r’\)\((r > r’)\) ,中心間の距離を\(d\)とすると
- 互いに外部にある ⇔ \(d > r + r’\)
- 外接する ⇔ \(d = r + r’\)
- 2点で交わる ⇔ \(r – r’ < d < r + r’\)
- 内接する ⇔ \(d = r – r’\)
- 一方が他方の内部 ⇔ \(d < r – r’\)
【図形と方程式】8.軌跡を求める手順
- 条件を満たす点\(P\) の座標を\(x, y\)として、図示する
- \(x, y\) の関係式を求める
- 逆に,②で求めた関係式(図形)上のすべての点\(P(x, y)\) が条件を満たすことを確かめる
【図形と方程式】9.不等式の表す領域
直線 \(y = ax + b\) について、
① 不等式 \(y > ax + b\)の表す領域は直線\(y = ax + b\)の上側の部分。ただし、境界線を含まない。
② 不等式 \(y < ax + b\)の表す領域は直線\(y = ax + b\)の下側の部分。ただし、境界線を含まない。
③ 不等式 \(y \leq ax + b\)の表す領域は直線\(y = ax + b\)の上側の部分。ただし、境界線を含む。
④ 不等式 \(y \geq ax + b\)の表す領域は直線\(y = ax + b\)の下側の部分。ただし、境界線を含む。
曲線\(y = f(x)\)について
①’ 不等式\(y > f(x)\)の表す領域は、曲線\(y = f(x)\)の上側の部分。ただし、境界線を含まない。
②’ 不等式\(y < f(x)\)の表す領域は、曲線\(y = f(x)\)の下側の部分。ただし、境界線を含まない。
曲線\(x = g(y)\)について、
③’ 不等式 \(x < g(y)\)の表す領域は、曲線の左側の部分。ただし、境界線を含まない。
④’ 不等式 \(x > g(y)\)の表す領域は、曲線の右側の部分。ただし、境界線を含まない。
円 \(C : (x – a)^2 + (y – b)^2 = r^2\) について、
① 不等式 \(C : (x – a)^2 + (y – b)^2 < r^2\)の表す領域は円\(C\) の内部。ただし、境界線を含まない。
② 不等式 \(C : (x – a)^2 + (y – b)^2 > r^2\)の表す領域は円\(C\) の外部。ただし、境界線を含まない。
【数学II】三角関数~公式集一覧~
【三角関数】1.弧度法
半径1の円の弧の長さに対する角度 → 弧度法
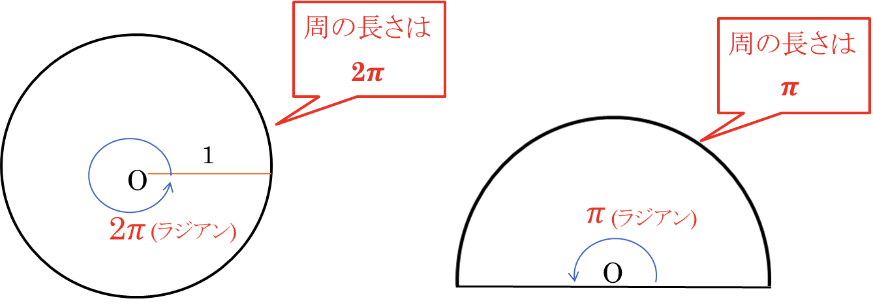
\(180^\circ = \pi\)ラジアン
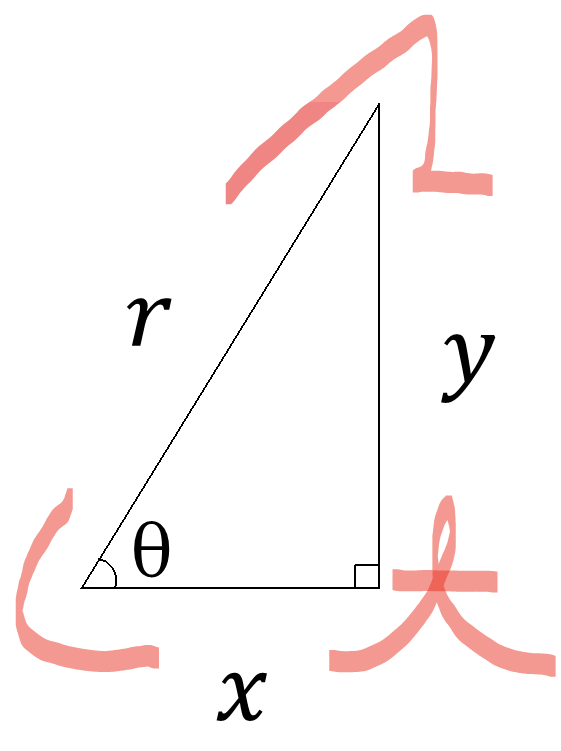
【三角関数】2.三角関数の定義
①\(\sin\theta = \displaystyle\frac{y}{r}\)
②\(\cos\theta = \displaystyle\frac{x}{r}\)
③\(\tan\theta = \displaystyle\frac{y}{x}\)
\(\theta\)の関数とみたとき、これらを三角関数という
【三角関数】3.三角関数の値
\(\cos\)の値 → 単位円上の\(x\)座標
\(\sin\)の値 → 単位円上の\(y\)座標
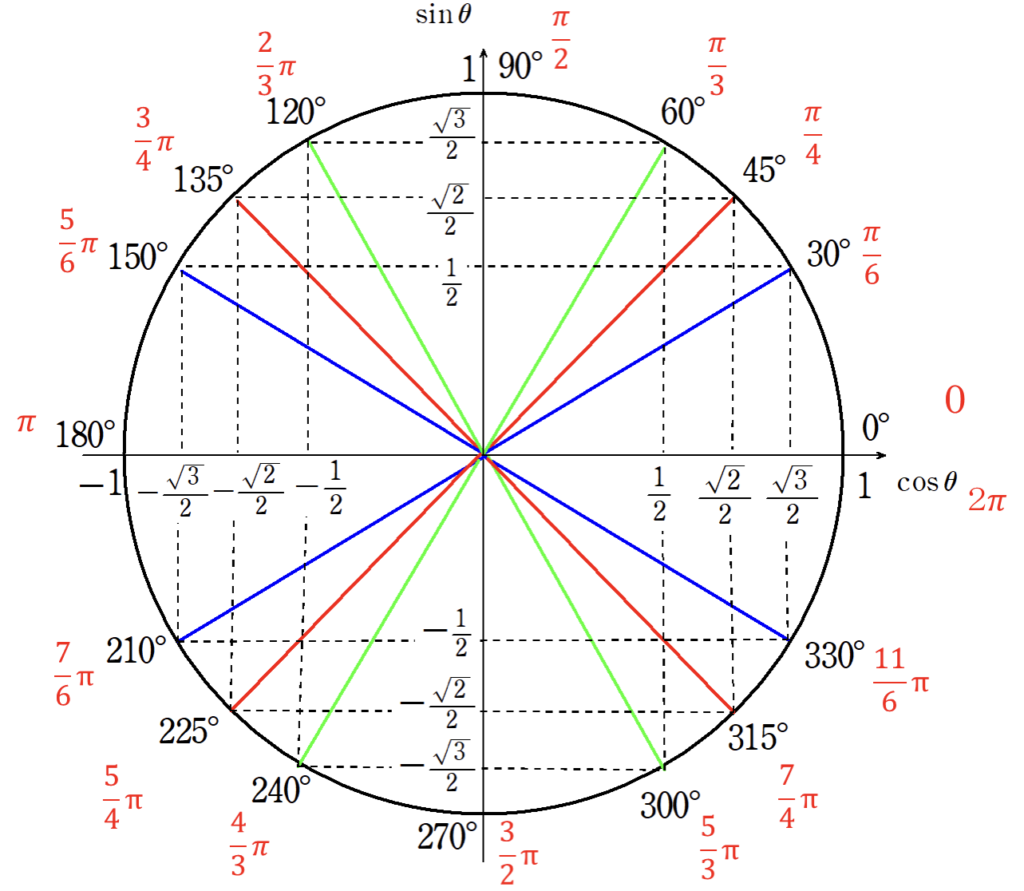
\(\tan\)の値 → 直線の傾き
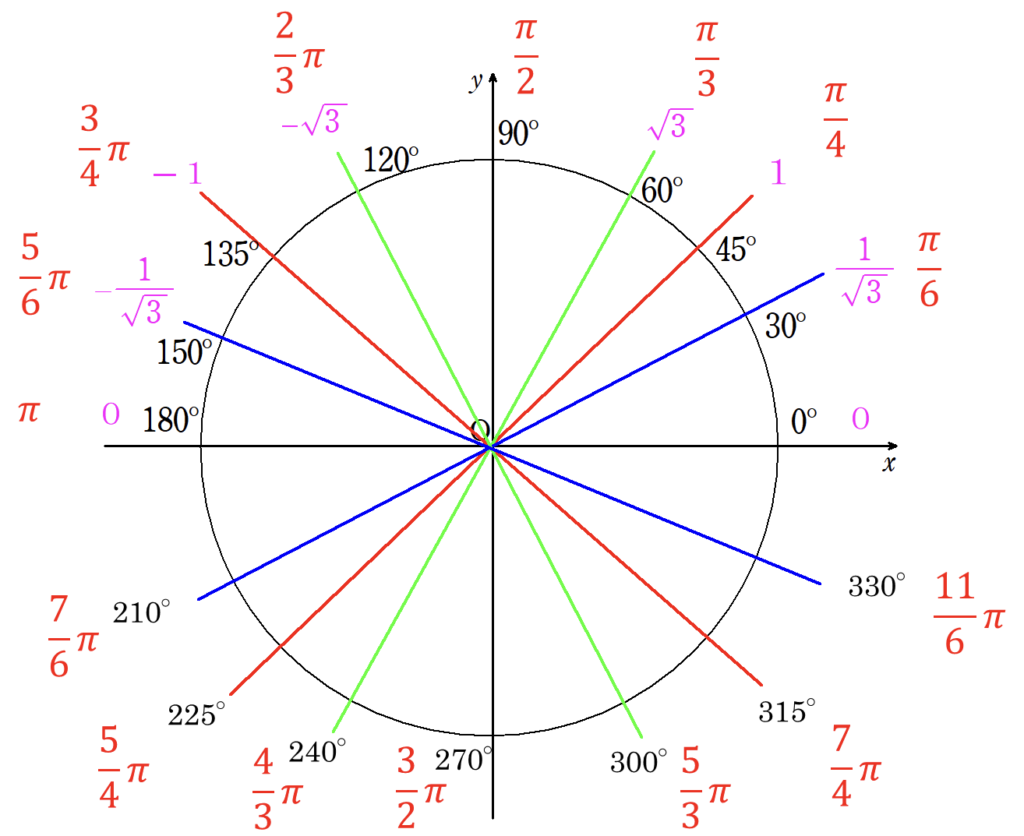
- \(-1 \leq \cos\theta \leq 1\)
- \(-1 \leq \sin\theta \leq 1\)
- \(\tan \theta\) → 実数全体
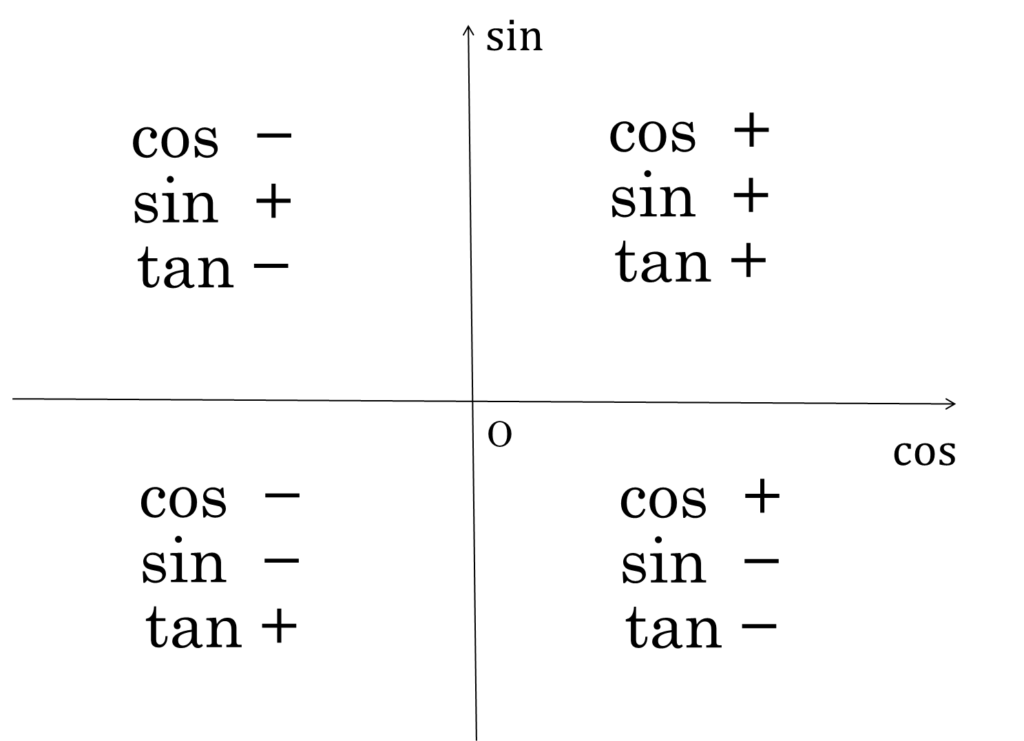
【三角関数】4.三角関数の相互関係
- \(\tan\theta=\displaystyle\frac{\sin\theta}{\cos\theta}\)
- \(\sin^2{\theta}+\cos^2{\theta}=1\)
- \(1+\tan^2{\theta}=\displaystyle\frac{1}{\cos^2{\theta}}\)
【三角関数】5.三角関数の性質
- \(\sin(\theta + 2n\pi) = \sin\theta\)
- \(\cos(\theta + 2n\pi) = \cos\theta\)
- \(\tan(\theta + n\pi) = \tan\theta\)
- \(\sin(-\theta) = -\sin\theta\)
- \(\cos(-\theta) = \cos\theta\)
- \(\tan(-\theta) = -\tan\theta\)
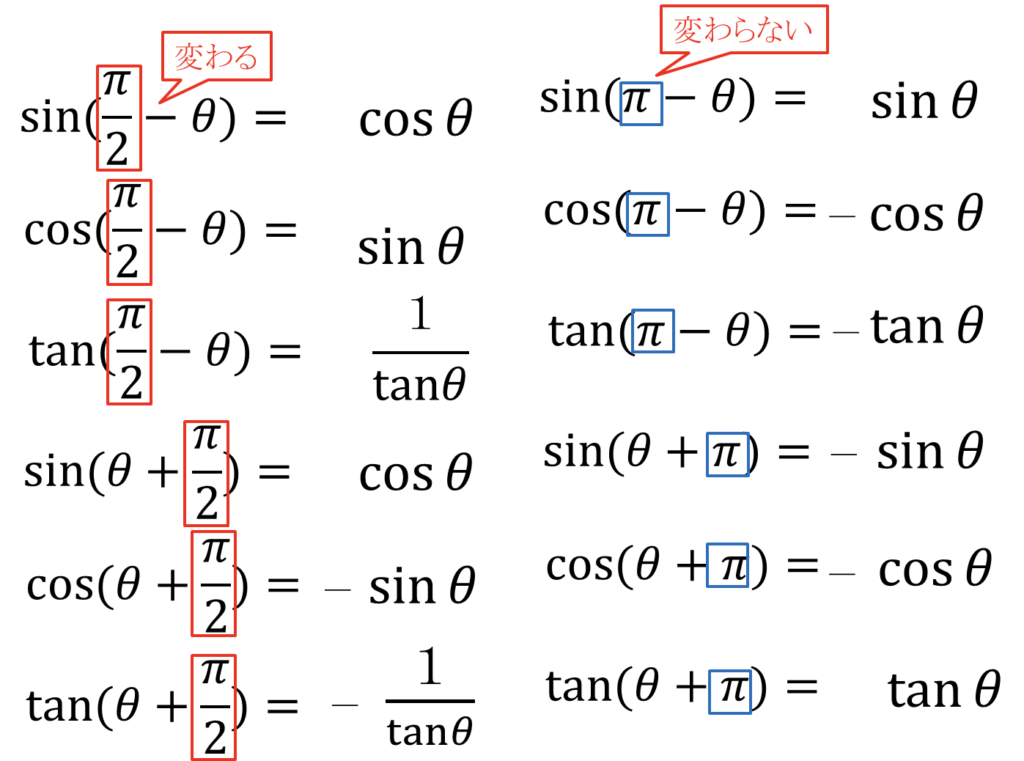
※\(\displaystyle\frac{\pi}{2}\)関連の加減 → 変わる
\(\sin ⇒ \cos\)
\(\cos ⇒ \sin\)
\(\tan ⇒ \displaystyle\frac{1}{\tan}\)
※\(\pi\)関連の加減 → 変わらない
\(\sin ⇒ \sin\)
\(\cos ⇒ \cos\)
\(\tan ⇒ \tan \)
と覚える
【三角関数】6.三角関数のグラフ
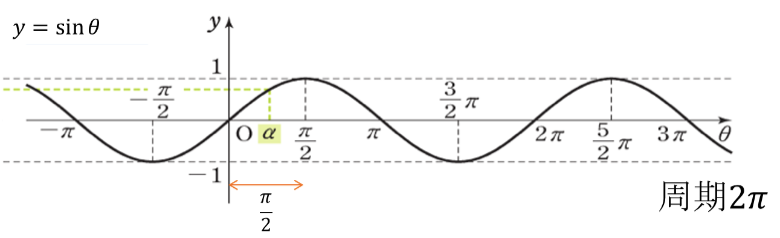
周期:\(2\pi\), 原点対称
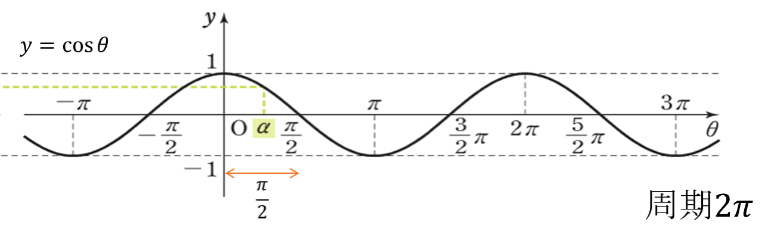
周期:\(2\pi\), \(y\)軸対称
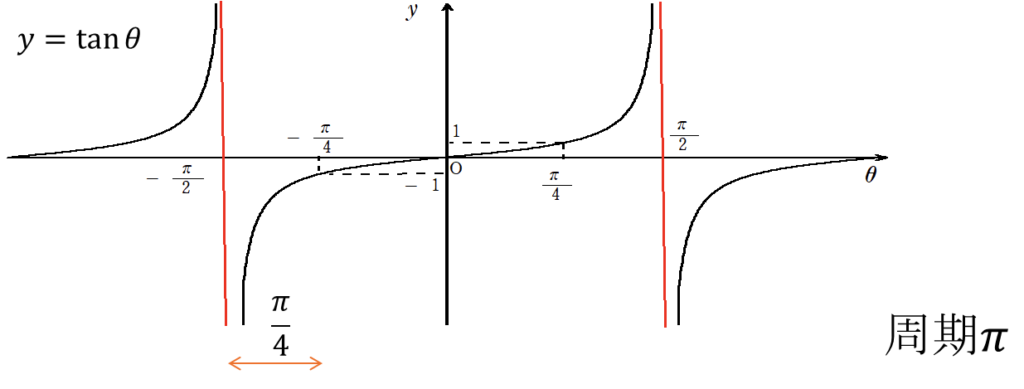
周期:\(\pi\), 原点対称
【三角関数】7.加法定理
- \(\sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta\)
- \(\sin(\alpha – \beta) = \sin\alpha\cos\beta – \cos\alpha\sin\beta\)
- \(\cos(\alpha + \beta) = \cos\alpha\cos\beta – \sin\alpha\sin\beta\)
- \(\cos(\alpha – \beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta\)
- \(\tan(\alpha+\beta) = \displaystyle\frac{\tan\alpha + \tan\beta}{1 – \tan\alpha \tan\beta}\)
- \(\tan(\alpha – \beta) = \displaystyle\frac{\tan\alpha – \tan\beta}{1 + \tan\alpha \tan\beta}\)
【三角関数】8.2倍角・半角の公式
①\(\sin2\theta = 2\sin\theta\cos\theta\)
②\(\cos2\theta = \cos^2\theta – \sin^2\theta\)
\(= 1 – 2\sin^2\theta\)
\(=2\cos^2\theta – 1\)
③\(\tan2\theta = \displaystyle\frac{2\tan\theta}{1 – \tan^2\theta}\)
①\(\sin^2\theta = \displaystyle\frac{1 – \cos2\theta}{2}\)
②\(\cos^2\theta = \displaystyle\frac{1 + \cos2\theta}{2}\)
③\(\tan^2\theta = \displaystyle\frac{1 – \cos2\theta}{1 + \cos2\theta }\)
①\(\sin^2\displaystyle\frac{\theta}{2} = \displaystyle\frac{1 – \cos\theta}{2}\)
②\(\cos^2\displaystyle\frac{\theta}{2} = \displaystyle\frac{1 + \cos\theta}{2}\)
③\(\tan^2\displaystyle\frac{\theta}{2} = \displaystyle\frac{1 – \cos\theta}{1 + \cos\theta }\)
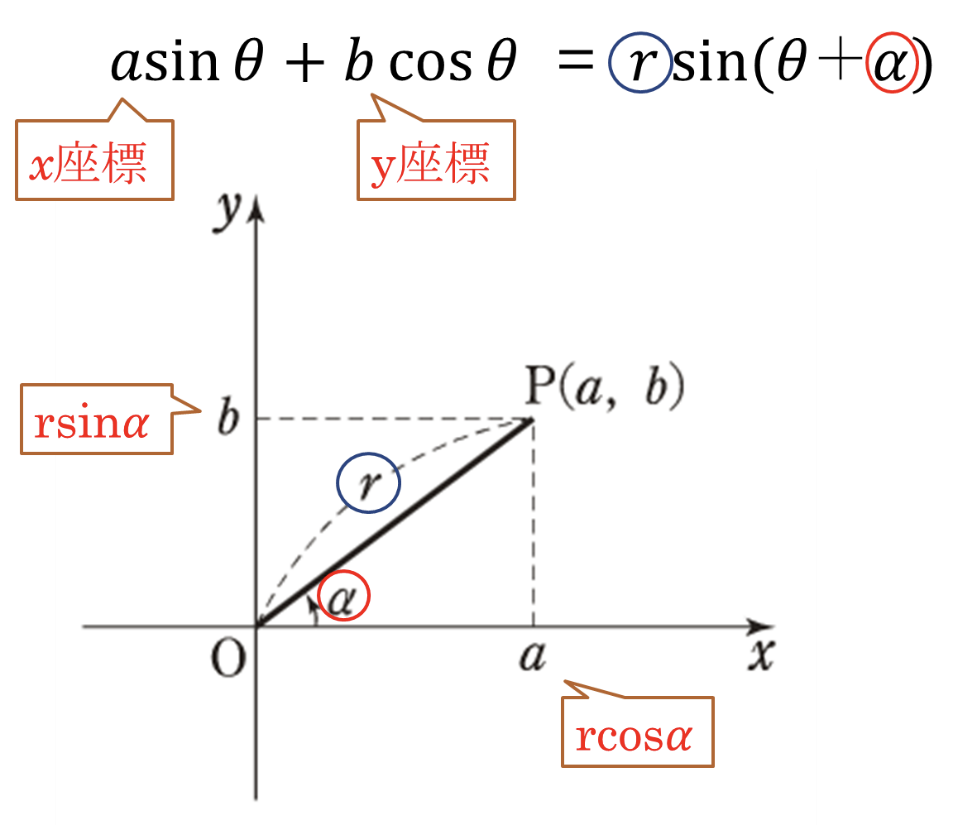
【三角関数】9.三角関数の合成
\(a\sin\theta + b\cos\theta = \sqrt{a^2 + b^2}\sin(\theta + \alpha)\)
※ただし、
\(\sin\alpha = \displaystyle\frac{b}{\sqrt{a^2 + b^2}}\)
\(\cos\alpha = \displaystyle\frac{a}{\sqrt{a^2 + b^2}}\)
【数学II】指数〜公式集一覧〜
【指数】1.累乗根の性質
\(a > 0, b > 0, m, n, p\) は正の整数とする。
- \((\sqrt[n]{a})^n = a\)
- \(\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{ab}\)
- \(\displaystyle\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\displaystyle\frac{a}{b}}\)
- \((\sqrt[n]{a})^m = \sqrt[n]{a^m}\)
- \(\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a}\)
- \(\sqrt[n]{a^m} = \sqrt[np]{a^{mp}}\)
【指数】2.有理数の指数
\(a > 0 , m, n\) は正の整数, \(r\) は正の有理数とする
\(a^{\frac{m}{n}} = \sqrt[n]{a^m}\)
※特に、\(a^{\frac{1}{n}} = \sqrt[n]{a}\), \(a^{-r} = \displaystyle\frac{1}{a^r}\)
【指数】3.指数法則
\(m , n \)は有理数とする。
① \(a^m \times a^n = a^{m+n}\)
② \((a^m)^n = a^{mn}\)
③ \((ab)^n =a^n b^n\)
※\(a^0 =1 \)
例題
次の計算をせよ。
① \(a^3 \times a^{-2} \)
② \((a^2)^{-3} \)
③ \((ab)^{-2} \)
解答
① \(a^3 \times a^{-2} = a^{3-2}=a \)
② \((a^2)^{-3} = a^{2 \times (-3)} =a^{-6} = \displaystyle\frac{1}{a^6}\)
③ \((ab)^{-2} = a^{-2} b^{-2} = \displaystyle\frac{1}{a^2b^2}\)
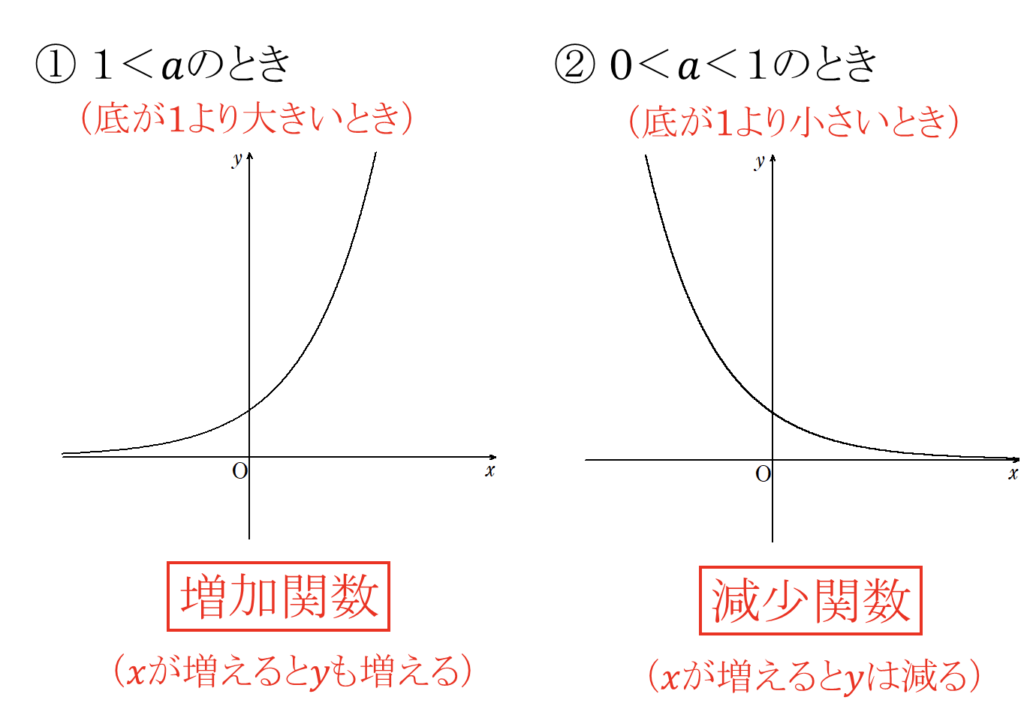
【指数】4.指数関数 \(y = a^x\) の性質
定義域:実数全体,値域:\(0 < y\)
①\(1 < a\)(底が1より大きい)とき
増加関数(\(x\)が増加すると\(y\)も増加)
②\(0 < a < 1\)(底が0より大きく、1より小さい)とき減少関数(\(x\)が減少すると\(y\)も減少)
【数学II】対数〜公式集一覧〜
【対数】1.対数の定義
\(a > 0, a \neq 1, M > 0\) とする。
\(a^p = M ⇔ p = \log_a M\)
※「\(M\) は\(a\) の何乗か(指数の逆)」の値を表す
【対数】2.対数の性質
\(a > 0, a \neq 1, M > , N > 0, k\) :実数 とする。
- \(\log_a a = 1\), \(\log_a 1 =0\), \(\log_a \displaystyle \frac{1}{a} = -1\)
- \(\log_a M + \log_a N = \log_a MN\)
- \(\log_a M – \log_a N = \log_a \displaystyle\frac{M}{N}\)
- \(\log_a M^k =k \log_aM\)
【対数】3.底の変換公式
\(a > 0, b > 0, c > 0\) で,\(a \neq 1, b \neq 1, c \neq 1\) のとき,
\(\log_ab = \displaystyle\frac{\log_cb}{\log_ca}\)
特に、\(\log_ab = \displaystyle\frac{1}{\log_ba}\)
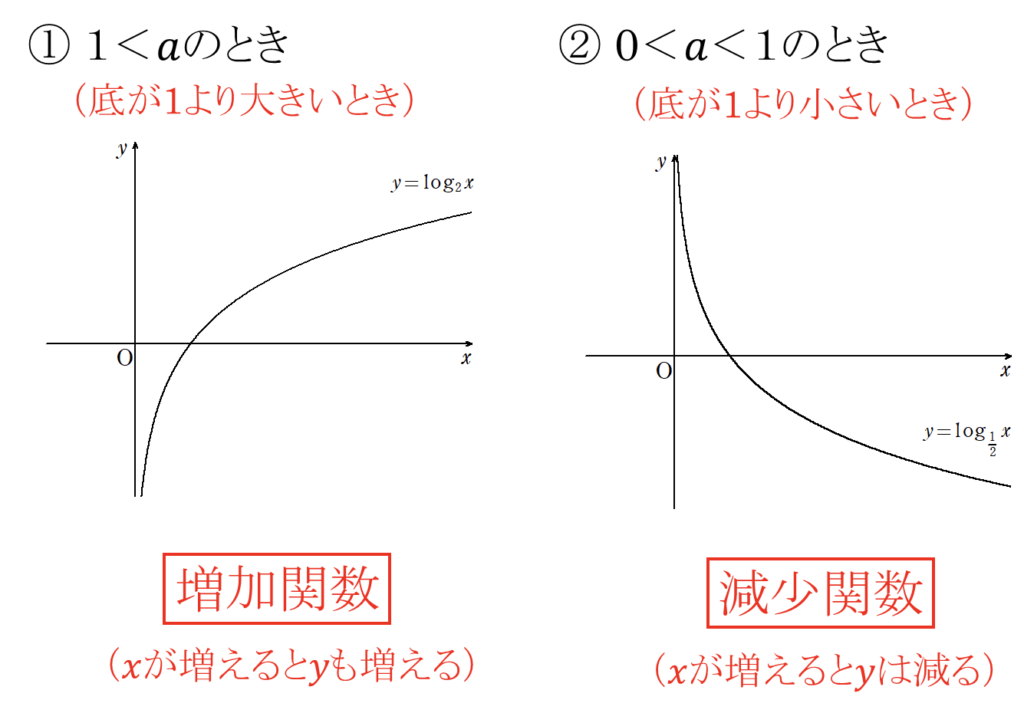
【対数】4.対数関数 \(y = \log_ax\) の性質
定義域:\(0 < x\),値域:実数全体
①\(1 < a\)(底が1より大きい)とき
増加関数(\(x\)が増加すると\(y\)も増加)
②\(0 < a < 1\)(底が0より大きく、1より小さい)とき減少関数(\(x\)が減少すると\(y\)も減少)
【対数】5.常用対数の利用
底が10 である対数を常用対数という
\(0 < x\) において
①\(n – 1 \leq \log_{10} x < n\)のとき、
\(x\) は\(n\)桁の整数
②\(-n \leq \log_{10} x < -(n-1) \)のとき、
\(x\) は小数第 \(n\) 位に初めて0でない数字が表れる
微分法〜公式集一覧〜
【微分法】1.微分係数
関数\(f(x)\) において,\(x\) が\(a\) から\(b\)まで変化するときの平均変化率は
\(\displaystyle \color{red}{\displaystyle\frac{f(b) – f(a)}{b – a}}\)
※平均変化率は中学における「変化の割合」と同じ
関数\(f(x)\) の\(x = a\) における微分係数\(f’(a)\)は
\(\displaystyle \color{red}{f’(a) = \lim\limits_{h \to 0}\displaystyle\frac{f(a+h) – f(a)}{h}}\)
※微分係数\(f’(a)\) は「関数\(y = f(x)\)の\(x = a\)における接線の傾き」を表す
【微分法】2.導関数
\(\displaystyle \color{red}{f’(x) = \lim\limits_{h \to 0}\displaystyle\frac{f(x+h) – f(x)}{h}}\)
※導関数\(f’(x)\) は「接線の傾きが出る式」を表す
\(n\)を正の整数、\(c\)を定数とするとき、
・\((x^n)’ = nx^{n-1}\)
・\((c)’ = 0 \)
\(k, l\) は定数とするとき、
- \(\{kf(x)\}’ = kf’(x)\)
- \(\{f(x) + g(x)\}’ = f’(x) + g’(x)\)
- \(\{kf(x) + lg(x)\}’ = kf’(x) + lg’(x)\)
【微分法】3.接線の方程式
曲線\(y = f(x)\)上の点\(A(a, f(a)) における接線の方程式は
\(\displaystyle \color{red}{y – f(a) = f’(a)(x – a)}\)
【微分法】4.関数の増減
関数\(y = f(x)\)において
①\(f’(x) > 0\) となる\(x\) の値の範囲ではグラフは増加する
※接線の傾きが正の範囲ではグラフは増加する
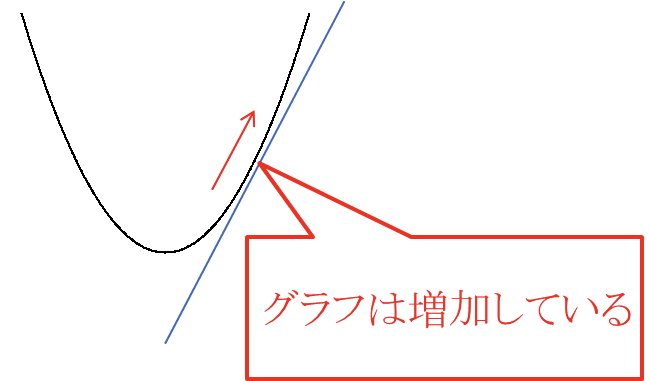
②\(f’(x) < 0\) となる\(x\) の値の範囲ではグラフは減少する
※接線の傾きが負の範囲ではグラフは減少する

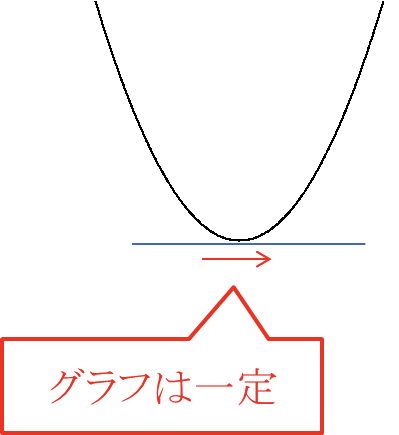
③\(f’(x) = 0\) となる\(x\) の値の範囲ではグラフは一定
※接線の傾きが0の部分ではグラフは一定となる
【微分法】5.関数の極大・極小
関数\(y = f(x)\) について
①\(f’(x)\) の符号が\(x = a\)の前後で正から負に変わるとき、
\(f(x)\)は\(x = a\)で極大になるといい、\(f(a)\)を極大値という
②\(f’(x)\) の符号が\(x = a\)の前後で負から正に変わるとき、
\(f(x)\)は\(x = a\)で極小になるといい、\(f(a)\)を極小値という
※極大値と極小値をまとめて、「極値」という。
関数\(f(x)\)が\(x = a\)で極値をとるとき、\(f’(a) = 0\)
※ただし、\(f’(a) = 0\)であっても、関数\(f(x)\)は\(x = a\)で極値をとるとは限らない
積分法〜公式集一覧〜
【積分法】1.不定積分
\(F’(x) = f(x)\) のとき
\(\int f(x) dx = F(x) + C\) (\(C\) は積分定数)
※\(F(x)\)を原始関数という
\(\int x^n dx = \displaystyle\frac{1}{n+1}x^{n+1} + C\) (\(C\) は積分定数)
\(k, l\) は定数とする
①\(\int kf(x) dx = k \int f(x) dx \)
②\(\int \{f(x) + g(x)\} dx = \int f(x) dx + \int g(x) dx \)
③\(\int \{kf(x) + lg(x)\} dx = k\int f(x) dx + l\int g(x) dx \)
【積分法】2.定積分
\(F’(x) = f(x)\) のとき
\(\int_{a}^{b} f(x) dx = \left[F(x)\right]_{a}^{b} = F(b) – F(a) \)
\(k\) は定数とする
①\(\int_{a}^{b} kf(x) dx = k \int_{a}^{b} f(x) dx \)
②\(\int_{a}^{b} \{f(x) + g(x)\} dx = \int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx \)
③\(\int_{a}^{a} f(x) dx = 0\)
④\(-\int_{a}^{b} f(x) dx = \int_{b}^{a} f(x) dx\)
⑤\(\int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx = \int_{a}^{b} f(x) dx\)
【積分法】3.定積分と微分法
\(\displaystyle \color{red}{\displaystyle\frac{d}{dx}\int_{a}^{x} f(t) dt = f(x)}\) (\(a\)は定数)
【積分法】4.面積
区間 \(a\leq x \leq b\) において
\(f(x) \geq 0\) のとき \(\displaystyle \color{red}{S = \int_{a}^{b}f(x)dx}\)
\(f(x) \leq 0\) のとき \(\displaystyle \color{red}{S = \int_{a}^{b}\{-f(x)\}dx}\)
区間 \(a\leq x \leq b\)で\(f(x) \geq g(x)\) のとき
\(\displaystyle \color{red}{S = \int_{a}^{b}\{f(x) – g(x) \}dx}\)
【積分法】5.面積公式
\(y = f(x)\) において
①\(f(x)\)が奇関数のとき
\(\displaystyle \color{red}{\int_{-a}^{a} f(x) dx = 0}\)
②\(f(x)\)が偶関数のとき
\(\displaystyle \color{red}{\int_{-a}^{a} f(x) dx = 2\int_{0}^{a} f(x) dx} \)
\(\displaystyle \color{red}{\int_{\alpha}^{\beta}(x – \alpha)(x – \beta)dx = -\displaystyle\frac{1}{6}(\beta – \alpha)^3 }\)
\(\displaystyle \color{red}{\int_{\alpha}^{\beta}(x – \alpha)^2 dx = \displaystyle\frac{1}{3}(\beta – \alpha)^3 }\)
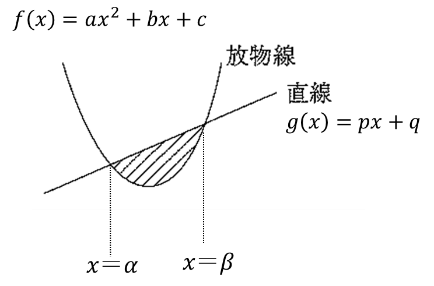
放物線 \( f(x) = ax^2+ bx + c\) と直線 \(g(x) = px+q\) の交点の \(x\) 座標を \(α, β(α<β)\)とするとき,この放物線と直線で囲まれた図形の面積 \(S\) は
\(\displaystyle \color{red}{S = \displaystyle\frac{|a|}{6}(\beta – \alpha)^3}\)
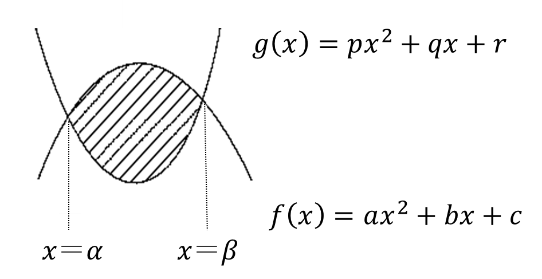
放物線 \( f(x) = ax^2+ bx + c\) と直線 \(g(x) = px^2+qx+r\) の交点の \(x\) 座標を \(α, β(α<β)\)とするとき,この2つの放物線で囲まれた図形の面積 \(S\) は
\(\displaystyle \color{red}{S = \displaystyle\frac{|a – p|}{6}(\beta – \alpha)^3}\)
放物線 \( f(x) = ax^2+ bx + c\) とその接線 \(g(x) = px+q\) の接点の \(x\) 座標を \(α\)とするとき,この放物線と接線および直線\(x = \beta\) で囲まれた図形の面積 \(S\) は
\(\displaystyle \color{red}{S = \displaystyle\frac{|a|}{3}(\beta – \alpha)^3}\)

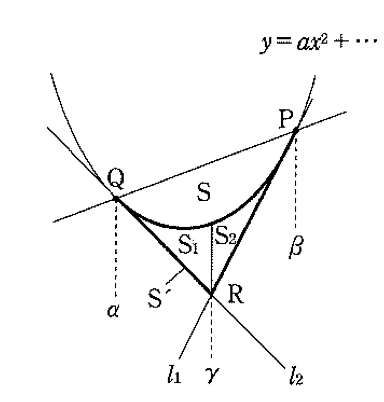
図において,放物線 \( y = ax^2 + bx + c \) と2本の接線の接点\(Q\),\(P\)の \(x\) 座標をそれぞれ \( \alpha, \beta \)(\( \alpha < \beta \))とすると,
① \(\displaystyle \color{red}{r = \displaystyle\frac{\alpha + \beta}{2}}\)
② \(\displaystyle \color{red}{S = \displaystyle\frac{|a|}{6}(\beta – \alpha)^3}\)
③ \(\displaystyle \color{red}{S’ = S_1 + S_2 = \displaystyle\frac{|a|}{12}(\beta – \alpha)^3}\)
④ \(\displaystyle \color{red}{S_1 = S_2 = \displaystyle\frac{|a|}{24}(\beta – \alpha)^3}\)
3次関数 \( y = f(x) \)(3次の係数が \( a \))とその接線 \( y = g(x) \) が,\( x = \alpha \) で接し,\( x = \beta \) で交わるとき,この3次関数と接線で囲まれた図形の面積 \( S \) は
\( \displaystyle \color{red}{ S = \frac{ |a| }{ 12 } ( \beta – \alpha)^4 } \)

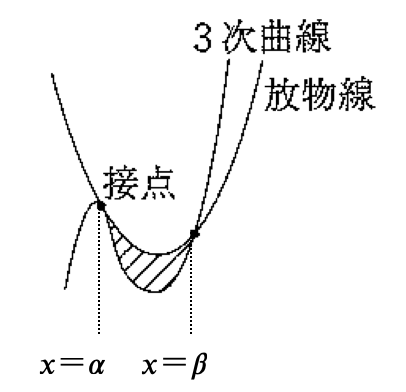
3次関数 \( y = f(x) \)(3次の係数が \( a \))と2次関数 \( y = g(x) \) が,\( x = \alpha \) で接し,\( x = \beta \) で交わるとき,この3次関数と接線で囲まれた図形の面積 \( S \) は
\( \displaystyle \color{red}{ S = \frac{ |a| }{ 12 } ( \beta – \alpha)^4 } \)







コメント