- 絶対値の外し方の基本
- 絶対値を含む方程式・不等式の基本的な解き方
- 絶対値を含む方程式・不等式の応用問題の解き方
絶対値を含む方程式・不等式の解き方
絶対値とは~外し方の基本~
数直線上における原点\(O(0)\) と点\(P(a)\) との距離を,実数\(a\) の絶対値といい、
実数\(a\) の絶対値であれば \(|a|\)
と表します。
例えば、
① \(|3| = 3\)
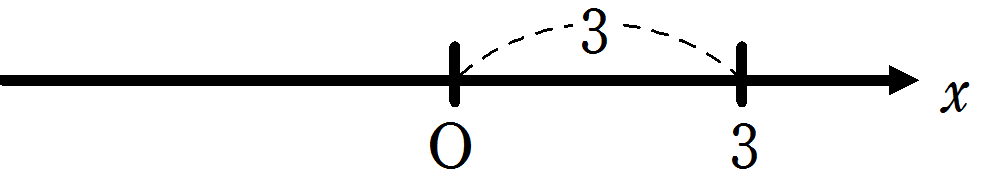
 シンスケ
シンスケ原点 O から \(3\) までの距離は\(3\)です。
したがって、絶対値の中が正のときは、絶対値はそのまま外せばOKです。
② \(|-2| = -(-2) = 2\)
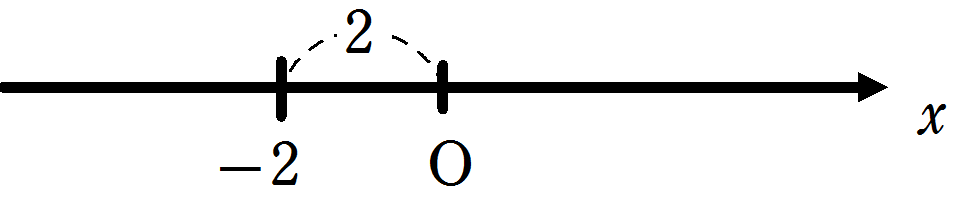
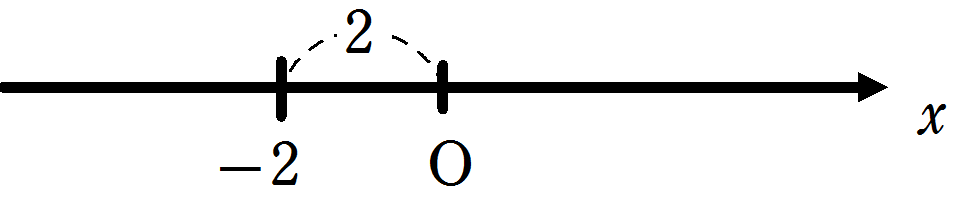



原点 O から \(-2\) までの距離は\(2\)です。
したがって、絶対値の中が負のときは、絶対値はマイナスをつけて外し、値は正になります。
したがって、基本的な絶対値の外し方は以下のようになります。
絶対値の外し方
絶対値の中が正 → そのまま外す
絶対値の中が負 → −をつけて外す
\( \begin{eqnarray} |x| = \begin{cases} x & (x \geq 0 のとき) \\ -x&(x \lt 0のとき) \end{cases}\end{eqnarray}\)
例題
次の値を求めよ。
① \(|-3|\)
② \(|3.7|\)
③ \(|\pi -4|\)
解答
① \(|-3| =-(-3)=3\)
② \(|3.7|=3.7\)
③ \(|\pi-4|=-(\pi-4)=-\pi+4\)
絶対値を含む方程式・不等式の基本的な解き方
絶対値を含む方程式・不等式の基本的な解き方をみていきましょう。
\(c\) が正の定数のとき
① 方程式 \(|x|=c\) の解は \(x=\pm c \)
② 不等式 \(|x|<c\) の解は \(-c<x<c\)
③ 不等式 \(|x|>c\) の解は \(x<-c, c<x \)
例題
次の方程式・不等式を解け。
① \(|x| = 2\)
② \(|x|<2\)
③ \(|x|>2\)
解答
① \(x=\pm 2 \)
② \(-2<x<2\)
③ \(x<-2, 2<x \)
① \(|x| = 2\)
⇒ 原点からの距離が \(2\) であるような \(x\) の値を求めよ。
という意味になります。


上記のように、原点からの距離が \(2\) であるような点の座標は \(2\) と \(-2\) の2つありますね。
したがって、
\(|x| = 2\) の解は
\(x=\pm 2 \)
となります。



マイナスの値もありますので注意しましょう。
② \(|x| < 2\)
⇒ 原点からの距離が \(2\) より小さいような \(x\) の値の範囲を求めよ。
という意味になります。
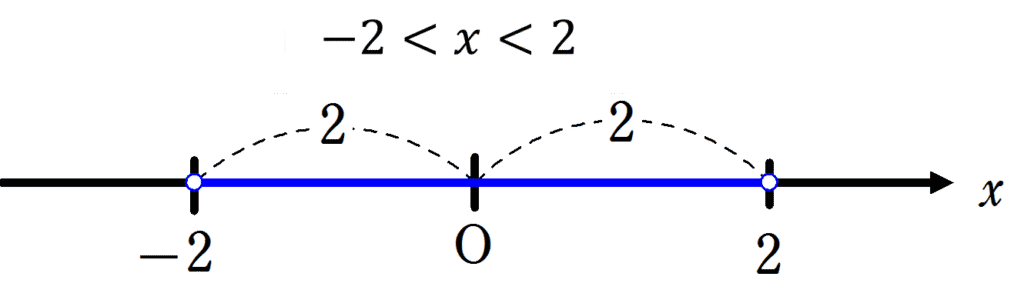

原点からの距離が \(2\) であるような点の座標は \(2\) と \(-2\) の2つありますが、このときより原点からの距離が小さい座標は上記のように\(-2\) と \(2\) の内側であればよいことがわかりますね。
したがって、
\(|x| < 2\) の解は
\(-2<x<2\)
となります。



「小さい場合は内側の範囲を答える」と覚えましょう。
① \(|x| > 2\)
⇒ 原点からの距離が \(2\) より大きいような \(x\) の値の範囲を求めよ。
という意味になります。
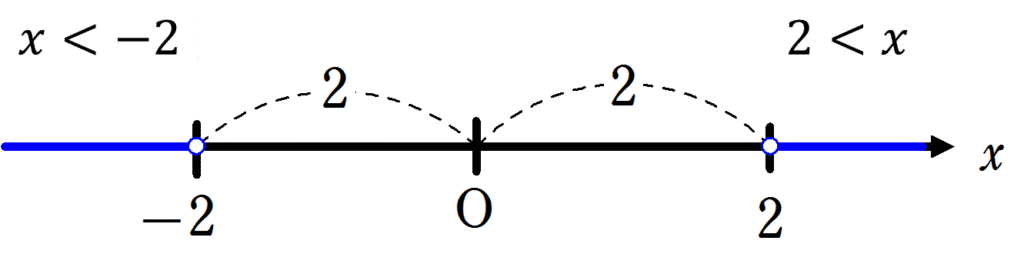

原点からの距離が \(2\) であるような点の座標は \(2\) と \(-2\) の2つありますが、このときより原点からの距離が大きい座標は上記のように\(-2\) と \(2\) の外側であればよいことがわかりますね。
したがって、
\(|x| > 2\) の解は
\(x < – 2, 2 < x\)
となります。



「大きい場合は外側の範囲を答える」と覚えましょう。
絶対値を含む方程式・不等式の応用問題の解き方
基本的な絶対値を含む方程式・不等式をふまえた上で応用問題にチャレンジしましょう。
応用問題 次の方程式・不等式を解け。
① \(|2x – 1| = 5\)
② \(|2x – 1| < 5\)
③ \(|2x – 1| > 5\)
POINT
①\(|2x – 1| = 5\)
\(2x – 1 = \pm 5\) ⇐ \( 2x – 1\) を1つの文字の塊\(A\)として考える
\(2x – 1 = -5 or 2x – 1 =5\)
\(2x = -4 or 2x = 6\)
\(x = -2, 3\)
②\(|2x – 1| < 5\)
\(-5 < 2x -1 < 5\) ⇐ \( 2x – 1\) を1つの文字の塊\(A\)として考える
\(-5+1 < 2x -1 +1 < 5 + 1\) ⇐ 1を足す
\(-4 < 2x < 6\) ⇐ 2で割る
\(-2 < x < 3\)
③\(|2x – 1| > 5\)
\(2x – 1 < -5, 5 < 2x -1\) ⇐ \( 2x – 1\) を1つの文字の塊\(A\)として考える
\(2x < -4 or 6 < 2x\)
\(x < -2 , 3 < x\)





コメント