 ラッシーくん
ラッシーくん2次関数の最大値・最小値がまったくわからないのですが求め方のコツはありますか?
このような疑問や悩みに答えます。
- 2次関数の最大値・最小値の基本的な求め方・考え方のコツ
- 定義域ありの2次関数の最大値・最小値の求め方
- 文字を含む2次関数の最大値・最小値の求め方
\(y=ax^2+bx+c\)
のように,左辺が \(x\) の 2 次式で表されるとき、\(y\)は\(x\) についての2次関数 といいます。
(ただし,\(a,b,c\) は定数で,\(a≠0\) )
今回は2次関数の最大値・最小値の基本的な求め方・考え方のコツを紹介します。



中学高校の数学教諭として15年以上現場で教えています。
特に、定義域ありの2次関数や、文字を含む2次関数の最大値・最小値の求め方がわからない方は参考にして下さい。
2次関数分野の基本公式はこちら
2次関数の最大値・最小値の求め方
基本的な考え方
まずは、2次関数の最大値・最小値の求め方の基本的な考え方をマスターしましょう。
結論、2次関数の最大値・最小値を求めるときの最大のコツは
条件を満たすグラフがかけるかどうか
という点になります。
そもそも、最大値・最小値とは、グラフの一番上の \(y\) 座標と一番下の \(y\) 座標を問われているにすぎません。
例えば、1次関数を例にしましょう。
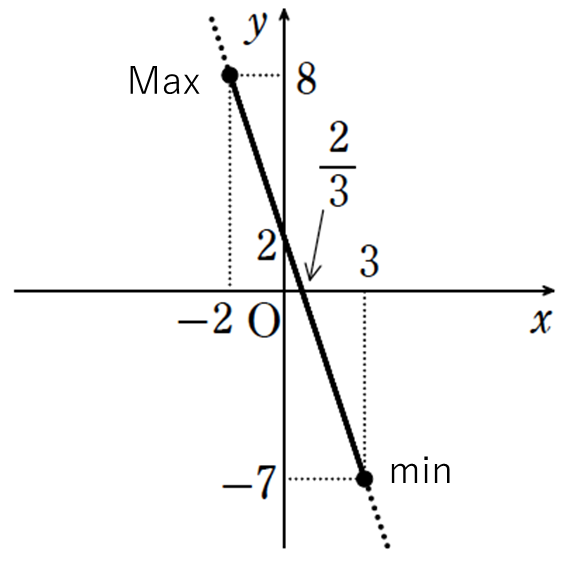

上記のような1次関数(直線)の場合はグラフの一番上の \(y\) 座標は 8 、グラフの一番下の \(y\) 座標は -7 であることは明らかですね。
したがって、
\(x=-2\) のとき最大値\(8\),\(x=3\) のとき最小値\(-7\)
がこの関数の最大値と最小値となります。
(※基本的には、最大値・最小値を与えるときの \(x\) の値も求めましょう。)



このように、2次関数に限らず、関数の最大値・最小値はグラフさえかけてしまえば、あとはグラフ上の一番上と一番下の値をみれば簡単に求めることができます。
したがって、「最大値・最小値がわからない」という場合はまずは条件を満たすグラフがかけるようになることが一番の近道となります。
定義域に制限がない場合の最大値・最小値
まずは、定義域に制限がない場合の2次関数の最大値・最小値を求めてみましょう。
基本的には、以下のステップを辿っていきます。
- 平方完成をする
- 頂点・軸・(端点を求める)
- グラフの概形をかく
- 最大値・最小値を求める
例題 2次関数\(y=2x^2-12x+22\)の最大値・最小値を求めよ。
\(y=2x^2-12x+22\)
\(y=2(x-3)^2+4\) より←①平方完成
頂点\((3, 4)\)
軸:直線\(x=3\) ←②頂点・軸を求める(今回はないが、定義域がある場合は端点も求める)
③グラフをかく
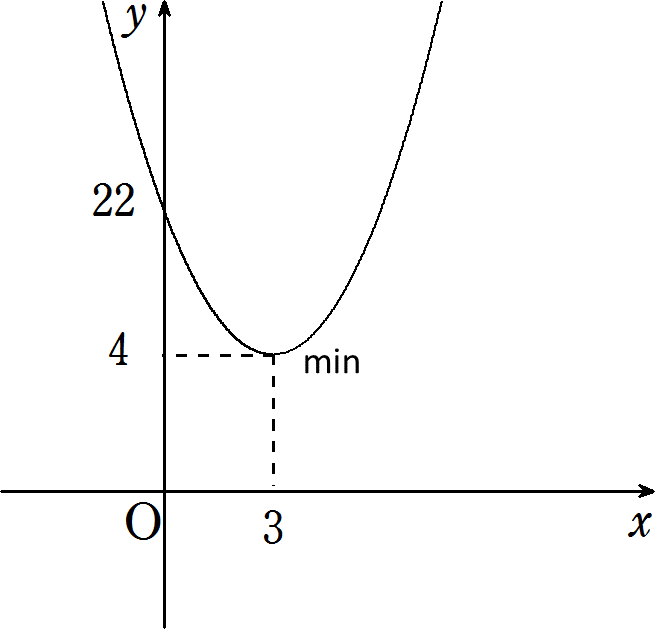
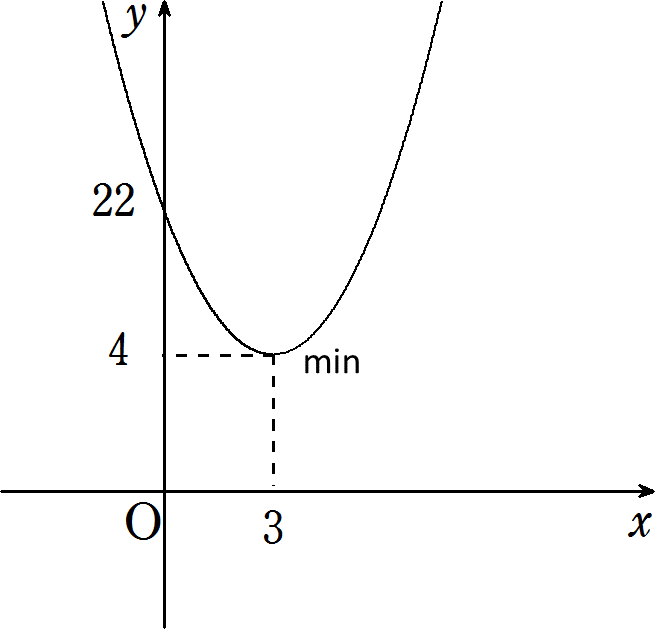
よって、グラフより
\(x=3 のとき最小値4\)
最大値なし←④最大値・最小値を求める。
1次関数と同様に、2次関数のグラフをかくことによって、最大値・最小値を求めることができます。
ただし、今回の問題の場合は、最小値は 4 と決まりますが、最大値に関してはどこまでも大きくなるため、特定の値は存在しません。
このような場合は、
最大値なし
のように解答しましょう。
例題 2次関数\(y=-2x^2+8x-5\)の最大値・最小値を求めよ。
\(y=-2x^2+8x-5\)
\(y=-2(x-2)^2+3\) より←①平方完成
頂点\((2, 3)\)
軸:直線\(x=2\) ←②頂点・軸
③グラフをかく
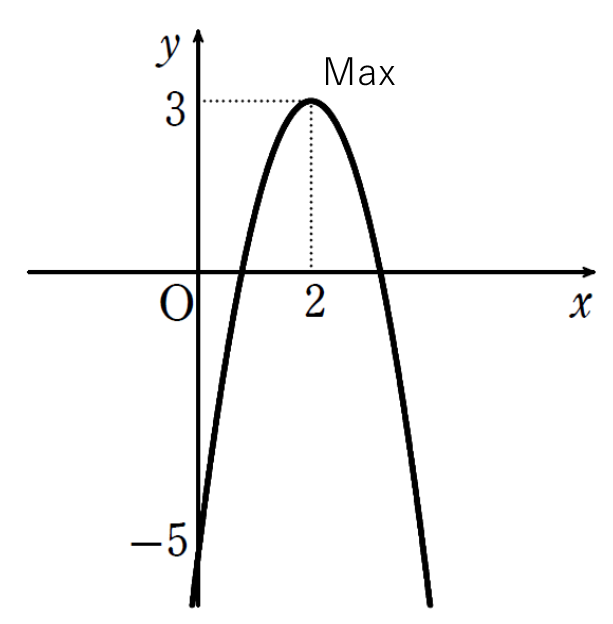

よって、グラフより
\(x=2のとき最大値3\)
最小値なし←④最大値・最小値を求める。
基本的な流れは同じですが、\(x^2\)の項の係数が負の場合は上に凸なグラフとなります。
今回は、最小値が決まらない(どこまでも小さくなる)ため、
最小値なし
となります。
定義域に制限がある場合の最大値・最小値
続いて、定義域に制限がある場合の最大値・最小値を求めてみましょう。



この定義域がある場合の最大値・最小値を理解することが重要ポイントになります。
例題 2次関数\(y=2x^2-12x+22(0 \leq x \leq 4) \)の最大値・最小値を求めよ。
\(y=2x^2-12x+22\)
\(y=2(x-3)^2+4\) より←①平方完成
頂点\((3, 4)\)
軸:直線\(x=3\)
端点:\(x=0のときy=22, x=4のときy=6\)←②頂点・軸・端点
③グラフをかく
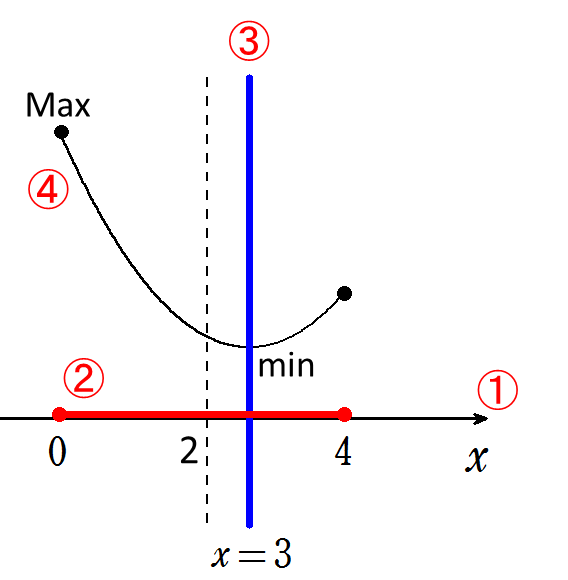

よって、グラフより
\(x=0のとき最大値22\)
\(x=3のとき最小値4\) ← ④最大値・最小値を求める。
定義域がある場合のグラフをかくときのポイント
定義域がある場合のグラフをかくときには上記のように、\(y\)軸をかかず、関数の軸に注目すると簡単にグラフをかくことができます。
手順としては以下になります。
- \(x\)軸をかく
- 定義域をかく
- 関数の軸をかく
- 概形をかく
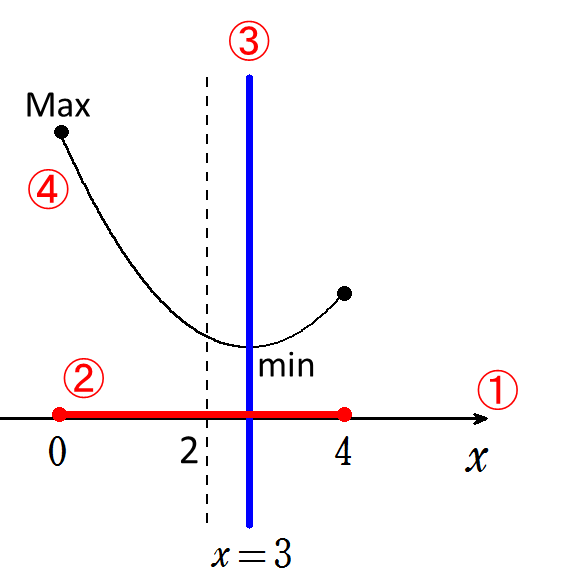

まず、\(x\)軸のみかく(\(y\) 軸はかかなくてOK)
定義域\((0 \leq x \leq 4) \)を\(x\)軸上にかく
軸:直線\(x=3\)を定義域上にかく。
※ただし、定義域の中央2(0~4の中点)よりも右側にかく
軸上に頂点がくるように、下に凸(\(x^2\)の係数に注意)な放物線をかく



ポイントは軸\(x=3\)を定義域上ある程度正確にかくことです。
特に、定義域の中央よりも軸が左側にあるか、右側にあるかが重要になります。
今回の場合は、軸が中央より右側にありますので、自然と端点の左端\(x=0\)のときが最大値になるような図になるはずです。
このように、定義域を含む場合はあえて、\(y\)軸は省略し、定義域と関数の軸の関係を考えることで驚くほど簡単に図示をすることができます。
また、上記でも明らかですが、実は2次関数の最大値・最小値は必ず以下の3つのいずれかでとります。
- 頂点
- 定義域の左端
- 定義域の右端
解答では、定義域の右端\(x=4\)のときの値も計算していますが、グラフからわかる通り、「頂点」「定義域の左橋」でとることが明らかであれば、これを計算しなくてもかまいません。



特に、大学入学共通テストなど解くスピードが求められ、かつ、途中過程も問われない場合は、この点を意識して、必要な部分のみ計算するのがおすすめです。
文字を含む場合の最大値・最小値
最後に文字を含む場合の最大値・最小値を求めてみましょう。



文字を含む場合は難易度が上がりますが、定義域がある場合の2次関数の最大値・最小値のグラフのかき方をしっかりとマスターしていればそこまで難しくありません。
応用問題 2次関数\(y=x^2-2ax+a^2+1(0 \leq x \leq 2) \)の最大値・最小値を求めよ。(\(aは定数とする\))
\(y=x^2-2ax+a^2+1\)
\(y=(x-a)^2+1\) より←①平方完成
頂点\((a, 1)\)
軸:直線\(x=a\)
端点:\(x=0\)のとき\(y=a^2+1\),
\(x=2\)のとき\(y=a^2-4a+5\)←②頂点・軸・端点を先に求めておく
③グラフをかく

よって、
①\(a\leq0\)のとき
\(x=2のとき最大値a^2-4a+5\)
\(x=0のとき最小値a^2+1\)
②\(0<a<1\)のとき
\(x=2のとき最大値a^2-4a+5\)
\(x=aのとき最小値1\)
③\(a=1\)のとき
\(x=0,2のとき最大値3\)
\(x=1のとき最小値1\)
④\(1<a<2\)のとき
\(x=0のとき最大値a^2-4a+5\)
\(x=aのとき最小値1\)
⑤\(2\leq a\)のとき
\(x=0のとき最大値a^2+1\)
\(x=2のとき最小値a^2-4a+5\)
まず、関数か定義域に文字を含む場合の最大値・最小値の求め方は原則的に場合分けが必要になります。



なぜなら、今回のように関数に文字がある場合は軸が\(x=a\)となり、一定の位置にいないからです。
定義域に文字を含む場合も同様に場合分けが必要です。
既に、記載した通り、2次関数は以下の3カ所のいずれかでしか最大値・最小値をとりません。
- 頂点
- 定義域の左端
- 定義域の右端
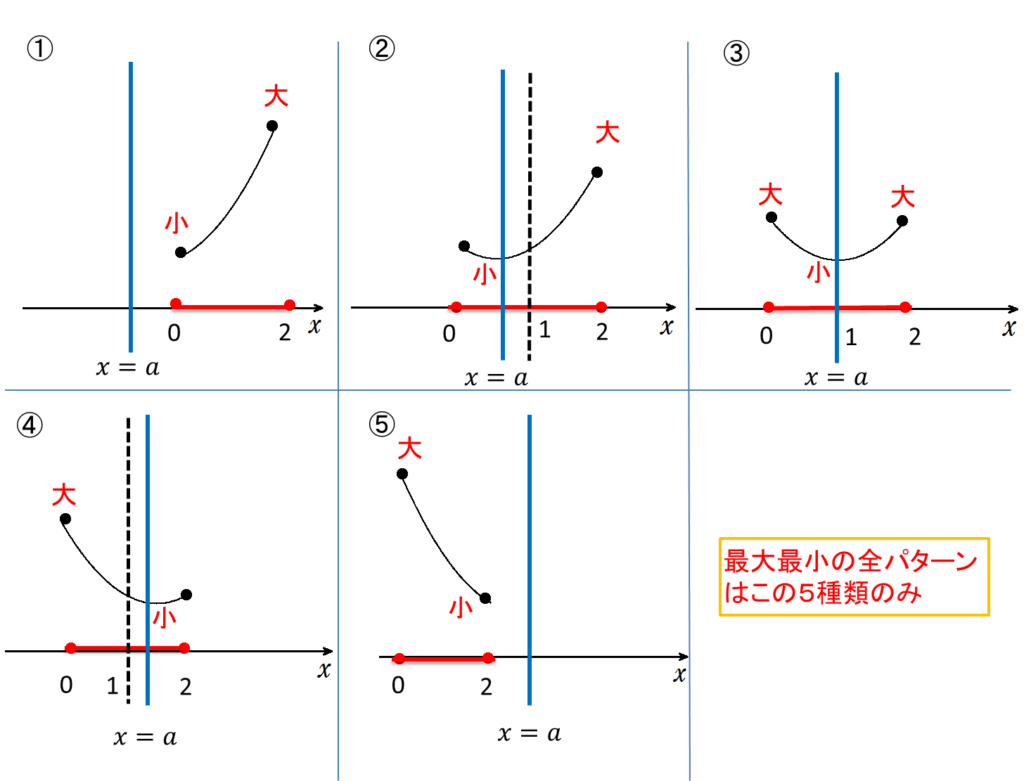
したがって、場合分けが最も多いときでも以下の5パターンのいずれかに必ずなります。





慣れないうちは、このような文字が入った最大値・最小値の問題はまずはこの5つのグラフをかくようにするのがおすすめです。
(条件に当てはまらないものは後から削除すればOK)
また、注意点としては、場合分けをした場合はそれがどのようなときなのか、書く必要があります。
上記は①~⑤と番号をふっていますが、必ずその後に(\(a=~のとき\))のような\(a\)のどのような範囲のときなのかを必ず書きましょう。
また、補足事項として、最終的な答えとしては上記の5パターンの解答の仕方でもかまいませんが、
最大値だけを問われている
最小値だけを問われている
このような問題の場合にも、5パターンすべてをかくのは大変ですよね。
上記の5パターンのグラフは最大値だけ、最小値だけを問われている場合は以下の3種類の場合分けだけできればOKです。
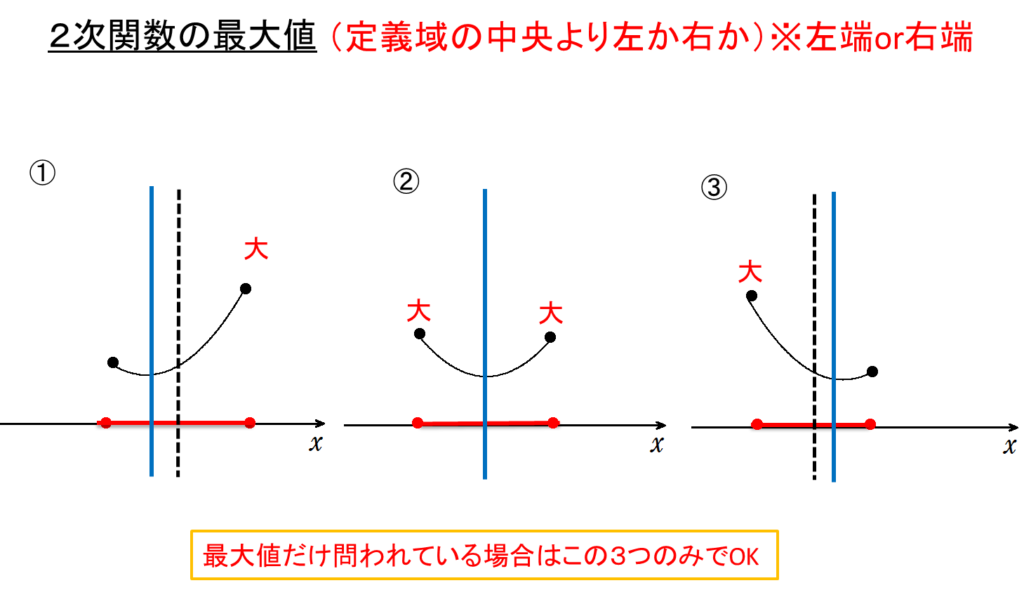

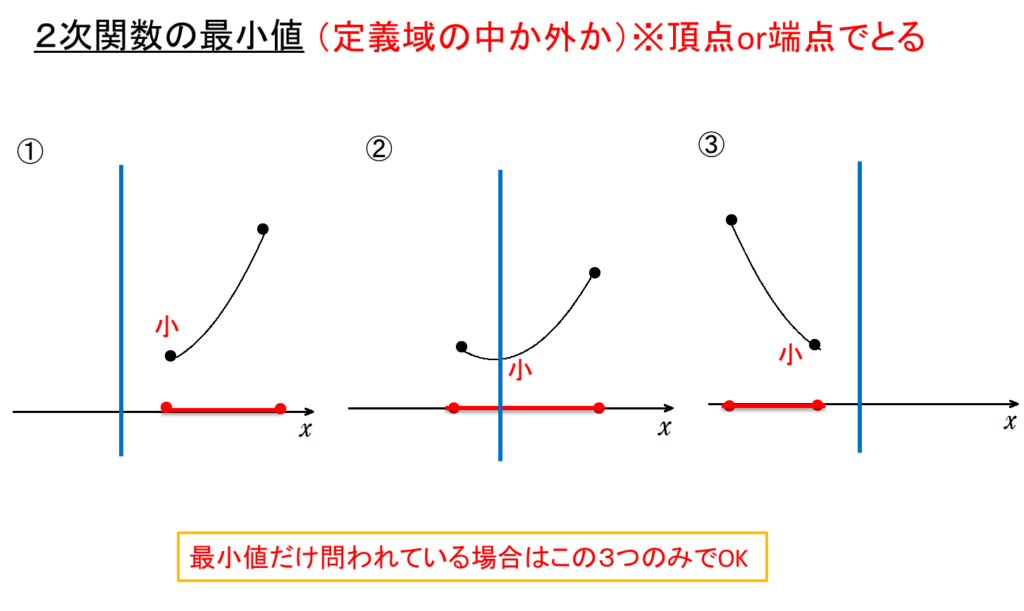

ただし、上に凸なグラフの場合は逆になるので注意!
最小値 → 定義域の中央より左か右か
最大値 → 定義域の中か外か
したがって、この応用問題においても、上記の5パターンの答え方ではなく、以下の書き方をしてもOKです。
①\(a<1\)のとき
\(x=2のとき最大値a^2-4a+5\) ←定義域の右端
②\(a=1\)のとき
\(x=0,2のとき最大値3\) ←定義域の左端と右端
③\(1< a\)のとき
\(x=0のとき最大値a^2+1\) ←定義域の左端
①\(a\leq0\)のとき
\(x=0のとき最小値a^2+1\) ←定義域の左端
②\(0<a<2\)のとき
\(x=aのとき最小値1\) ←頂点
⑤\(2\leq a\)のとき
\(x=2のとき最小値a^2-4a+5\) ←定義域の右端



問題集の解説などでは、それぞれ上記の3パターンずつで紹介されていることが多いです。
適宜、使い分けられるようになるのが一番良いですが、慣れるまではまずは先に紹介した5パターンの図示ができるようになりましょう。
今回は紹介しませんが、定義域に文字を含む問題でも同様の解き方でできます。試してみて下さい。
2次関数の最大値・最小値の求め方はまずはグラフから!
今回は2次関数の最大値・最小値の求め方を紹介しました。
最も大切なことは
条件を満たすグラフがかけるかどうか
という点になります。
数学が得意な人は一見すると、グラフをかかないで求められているように思われがちですが、必ず頭の中で図をイメージしながら解いています。
このポイントをおさえずに、応用問題に取り組もうするとわからなくなってしまいますので、注意しましょう。
また、数学の学習法を以下で紹介しています。
学習の仕方がわからない場合は是非チェックをしてみて下さい。




コメント