 ラッシーくん
ラッシーくん2次不等式がまったくわからないのですが解き方のコツはありますか?
このような疑問や悩みに答えます。



中学高校で15年以上数学教諭として現場で教えています。
- 2次不等式の解き方の基本
- 2次不等式の解き方の注意点
- 2次不等式の応用問題を解こう
\(ax^2+bx+c\geq0 , ax^2+bx+c\lt0\)
などのように,左辺が \(x\) の 2 次式になる不等式を,\(x\) についての2次不等式 といいます。
(ただし,\(a,b,c\) は定数で,\(a≠0\) )
今回は2次不等式の解き方の基本と注意点、応用問題の解き方について、解説していきます。
2次不等式・2次関数分野の基本公式はこちら
2次不等式の解き方の基本
まずは、2次不等式の解き方の基本をマスターしましょう。
応用問題もこの考え方をしっかりマスターしていることがとても重要です。
基本的な考え方
結論、2次等式を解くときの最大のコツは
両辺に\(y=\)を入れて、グラフ同士の関係性を考える
という点になります。
具体的な例をみていきましょう。
例題 \(x^2-2x-3\lt0\)を解け。
この不等式の両辺に\(y=\)を入れると以下のようになります。
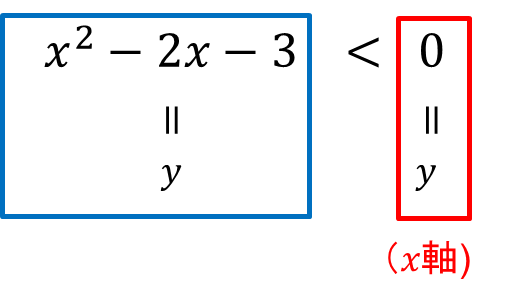




左辺は \(y=x^2-2x-3\) という2次関数、右辺は \(y=0\)すなわち\(x軸\)ですね。
したがって、この問題は
2次関数 \(y=x^2-2x-3\) が \(x\)軸より小さい(下側にあるような)\(x\)の範囲を求めよ。
このように言い換えることができるのです。
\(y=x^2-2x-3\)と\(x\)軸との交点を求めると
\(x^2-2x-3=0\)より
\((x+1)(x-3)=0\)
\(x=-1, 3\)
より、求める範囲を図示すると以下赤線部分になります。
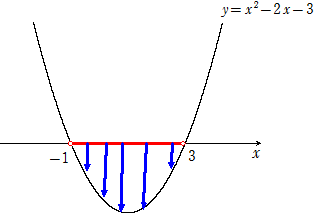

したがって、求める\(x\)の範囲は
\(-1<x<3\)
となります。
主な2次不等式のパターン
2次不等式には主に以下の3パターンがあります。
- \(x\)軸と2点で交わる
- \(x\)軸と接する
- \(x\)軸と交わらない
ただし、これらは\(x\)軸との関係性という意味では上記のようにパターン化されることが多いですが、基本的な考え方は
両辺に\(y=\)を入れて、グラフ同士の関係性を考える
という点で変わりません。



ここでも紹介はしますが、「このパターンは~このやり方」というように、覚える必要は全くありませんので、あくまでも基本に従って解いて下さい。
パターン①\(x\)軸と2点で交わる
例 \(x^2-2x-3>0\)を解け。
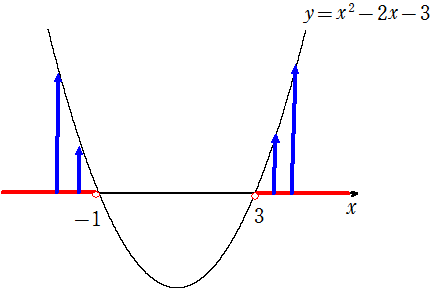

したがって、求める\(x\)の範囲は
\(x<-1,3<x\)



基本的には求めた\(x\)軸との交点の外側が答えの範囲となります。
例 \(x^2-2x-3<0\)を解け。(例題と同じ問題)
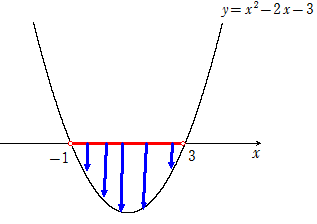

したがって、求める\(x\)の範囲は
\(-1<x<3\)



基本的には求めた\(x\)軸との交点の内側が答えの範囲となります。
パターン②\(x\)軸と接する(1点で交わる)
例えば、\(x^2-2x+1>0\)は
\(y=x^2-2x+1\)と\(x\)軸との交点を求めると
\(x^2-2x+1=0\)より
\((x-1)^2=0\)
\(x=1\)
したがって、2次関数が\(x\)軸と接する(1点で交わる)グラフとなるため、次のようになります。
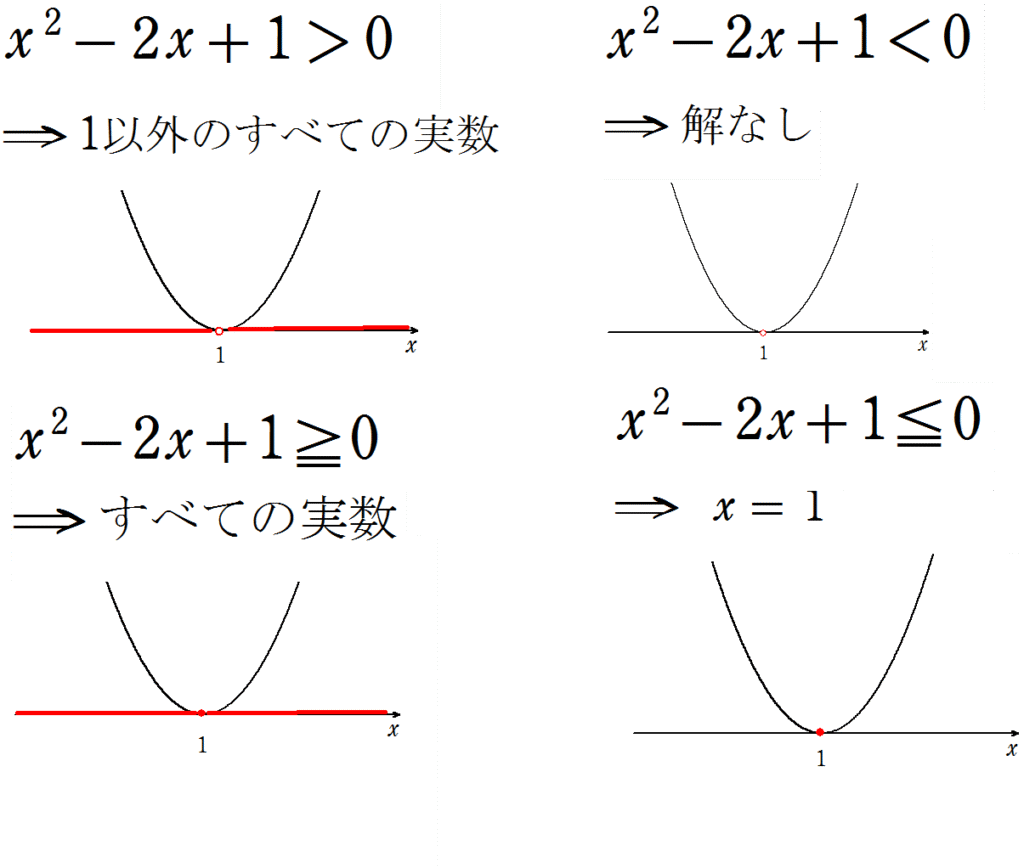
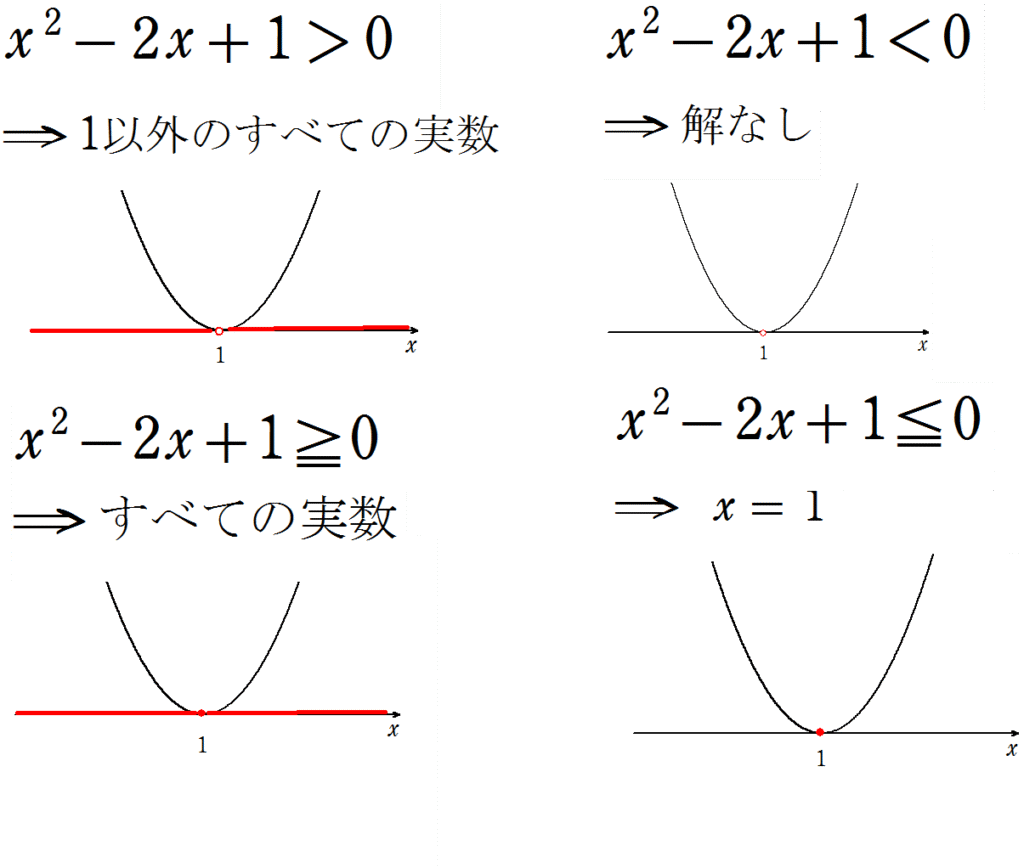
パターン③\(x\)軸と交わらない(交点なし)
例えば、\(x^2-2x+2>0\)は
方程式\(x^2-2x+2=0\)の判別式\(D<0\)より、\(x\)軸との共有点はなしとなります。
したがって、次のようになります。
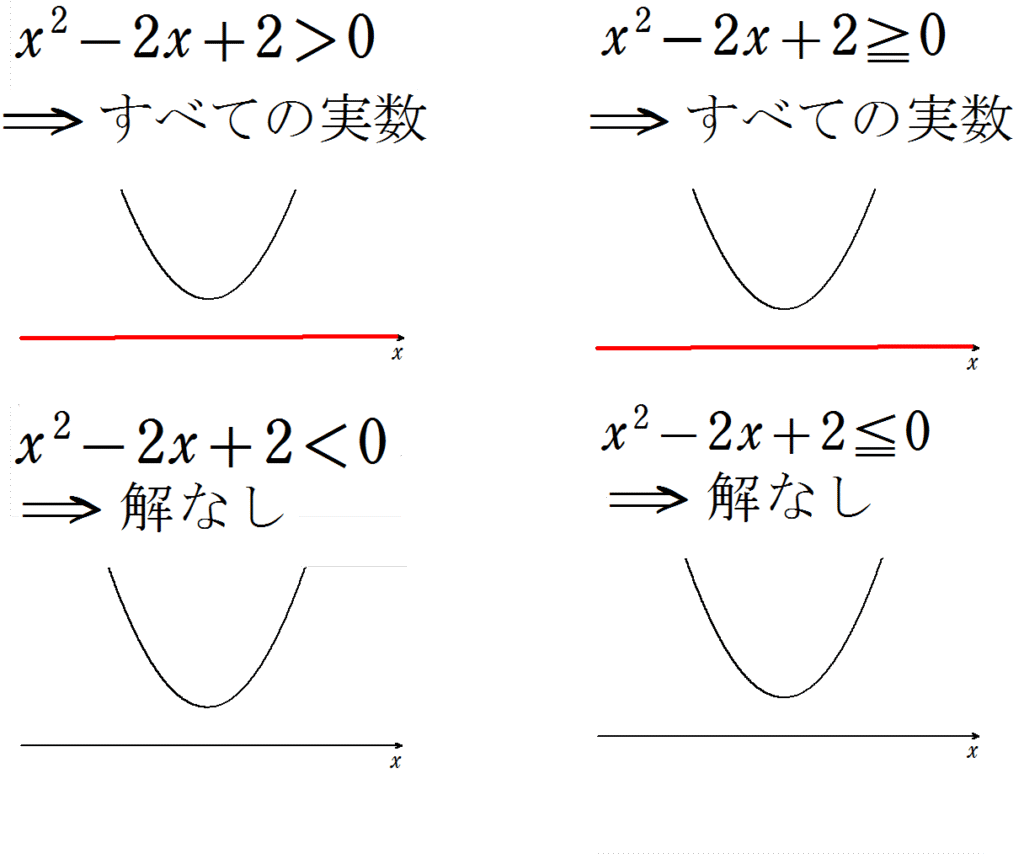

2次不等式の解き方の注意点
応用問題に触れる前に、ここで2次不等式の解き方の注意点を3点あげます。
- 慣れないうちは楽をした解き方をしない
- パターンで覚えない
- 1次不等式のような解き方はできない
慣れないうちは楽をした解き方をしない
まず、1点目は「慣れないうちは楽をした解き方をしない」という点です。
楽をした解き方というのは例えば、以下のような解き方になります。
例題 \(x^2-2x-3\lt0\)を解け。
\(x^2-2x-3<0\)より \((x+1)(x-3)<0\)
すなわち
\(-1<x<3\)
特に、\(x\)軸と異なる2点で交わる場合は、要は\(x\)軸との交点の内側が解となるため、上記のようにそのまま因数分解をして解く人が多いかと思います。



実際、私も普段は上記で解きます。
しかしながら、本記事でも紹介したような根本的な基本を理解せずに上記で慣れてしまった場合、応用問題に全く対応できなくなってしまいます。
例えば、以下のような問題です。
問題 2次不等式 \(x^2+2mx+2m+3>0 \)の解がすべての実数であるとき,定数\(m\) の値の範囲を求めよ。
このように、文字\(m\)が入った2次不等式や因数分解できない問題が応用問題では非常に多く出題されますが、楽な解き方で慣れてしまうとこのような問題には一切対応できなくなってしまうので注意しましょう。
したがって、面倒なようでも、しっかりと定着するまでは、
両辺に\(y=\)を入れて、グラフ同士の関係性を考える
という基本に忠実に解き、図(グラフ)に関してもその都度かくようにすることをおすすめします。
パターンで覚えようとしない
2つ目が「パターンで覚えようとしない」ようにしましょう。
- \(x\)軸と2点で交わる
- \(x\)軸と接する
- \(x\)軸と交わらない
この記事でも上記の3パターンを紹介しましたが、\(x\)軸との関係性という意味ではパターン化されることが多いものの根本的な考え方は変わりません。
数学が苦手な人ほどパターンを覚えようとする傾向がありますが、これは全くの逆効果になります。
数学の範囲は広いですし、公式もたくさん出てきますので、
なるべく覚えようとせず、考えながら解く
ということを大切にしましょう。



公式に関してもなるべくは、自ら考えて導き出せるようになる方が良いです。
1次不等式のような解き方はできない
3つ目はあくまでも2次不等式の解き方は本記事でも紹介したやり方になりますので、
「1次不等式のような解き方はしない」
ように注意しましょう。
これは、私が教えていても非常に多いのですが、例えば以下のような問題では注意が必要です。
例 \(x^2-4\lt0\)を解け。
上記のような問題の際に、
\(x^2-4>0\)
\(x^2>4\)
\(x>±2\)
このように解こうとする人が、経験上かなりいますが、このようなことは絶対にしないようにしましょう。



\(x>±2\)は\(x>-2\)かつ\(x>2\)なので、共通部分は\(x>2\)となってしまいます。
方程式の場合は\(x=±2\)と書くこともありますが、そもそも不等式でこの書き方は基本的にはしません。
2次不等式の応用問題の解き方
最後に、以上の基本事項と注意点をおさえつつ、一般的な2次不等式の応用問題に触れていきましょう。
問題 2次不等式 \(x^2+2mx+2m+3>0 \)の解がすべての実数であるとき,定数 \(m\) の値の範囲を求めよ。



注意点の欄で紹介した問題です。
ここまで説明した通り、
両辺に\(y=\)を入れて、グラフ同士の関係性を考える
と以下のようになります。


したがって、この問題は
2次関数 \(y=x^2+2mx+2m+3\) が \(x\)軸より常に大きい(上側にあるような)\(x\)の範囲を求めよ。
このように言い換えることができます。
条件を満たすような図(グラフ)は以下のようになります。
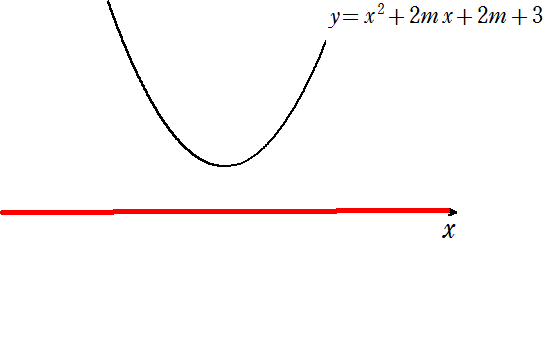

この状態であれば、2次関数が\(x\)軸より常に上側にあり、解がすべての実数になることがわかるかと思います。
そして、この状態になるときは、
2次関数 \(y=x^2+2mx+2m+3\) が \(x\)軸と交わらない
と言い換えることができるので、
結論
\(x^2+2mx+2m+3=0\)の判別式\(D<0\)となればOKとなることがわかりますね。
したがって、
\(D/4=m^2-(2m+3)<0\)
\((m^2-2m-3)<0\) … (*)
\((m+1)(m-3)<0\)
\(-1<m<3\)
となります。
(ここでは簡略化のため、簡単な方法で2次不等式(*)を解いていますが、ここでも慣れないうちはしっかりと図示をしましょう)
2次不等式は解き方の基本が重要!考え方にまずは慣れよう!
今回は2次不等式の解き方を紹介しましたが、最も大切なことは
両辺に\(y=\)を入れて、グラフ同士の関係性を考える
という点になります。
このポイントをおさえずに、応用問題に取り組もうすると途端にわからなくなってしまいますので、注意しましょう。
実は今回出てきたような
方程式や不等式を図示する(グラフ化する)
という考え方は、2次不等式の分野だけではなく、数学Ⅱ、数学Ⅲでも通用する方法です。
応用や発展レベルの問題では、方程式・不等式のような式扱いで解くのではなく、いかに図示をするかが重要になってきますので、ここでしっかり学んでおいて下さいね。
また、数学の学習法を以下で紹介しています。
学習の仕方がわからない場合は是非チェックをしてみて下さい。








コメント