ここでは、【数学I】「数と式」でよく利用する公式(基礎知識)と例題を一覧にしています。
1.多項式の乗法
\(m , n \)は正の整数とする。
① \(a^m \times a^n = a^{m+n}\)
② \((a^m)^n = a^{mn}\)
③ \((ab)^n =a^n b^n\)
※\(a^0 =1 \)
例題
次の計算をせよ。
① \(a^3 \times a^2 \)
② \((a^4)^2 \)
③ \((ab)^3 \)
解答
① \(a^3 \times a^2 = a^{3+2}=a^5 \)
② \((a^4)^2 = a^{4 \times 2} =a^8\)
③ \((ab)^3 =a^3 b^3\)
①\((a+b)^2 = a^2 + 2ab + b^2\)
\((a-b)^2 = a^2 – 2ab + b^2 \)
②\((a+b) (a-b) = a^2 – b^2 \)
③\((x+a) (x+b) = x^2 + (a+b) x + ab \)
④\((ax+b)(cx+d) = acx^2 + (ad+bc) x + bd\)
例題
次の式を展開せよ。
① \((x+3y)^2 \)
② \((2a+b) (2a-b) \)
③ \((x+3) (x+2) \)
④ \((2x+3) (3x-5) \)
解答
① \((x+3y)^2 = x^2 + 2・x・(3y) + (3y)^2 = x^2 + 6xy + 9y^2\)
② \((2a+b) (2a-b) = (2a)^2 – b^2= 4a^2 – b^2 \)
③ \((x+3) (x+2) = x^2 + (3+2) x + 3 \cdot 2 = x^2 + 5 x + 6 \)
④ \((2x+3) (3x-5) \)
\(= 2 \cdot 3 x^2 + \{ 2 \cdot (-5) + 3 \cdot 3 \} x + 3 \cdot (-5) \)
\(= 6x^2 – x -15 \)
\((a+b+c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca\)
例題
次の式を展開せよ。
\((x – 2y + z)^2 \)
解答
\((x – 2y + z)^2 \)
\(= x^2 + (-2y)^2 + z^2\)
\(+2 \cdot x \cdot (-2y)+2 \cdot (-2y) \cdot z +2 \cdot z \cdot x\)
\(= x^2 + 4y^2 + z^2 – 4xy – 4yz + 2zx\)
2.因数分解
\(AB + AC = A (B+C) \)
例題
次の式を因数分解せよ。
\(3a^3b-9a^2b^2 \)
解答
\(3a^3b-9a^2b^2 = 3a^2b(a-3b)\)
① \(a^2 + 2ab + b^2 = (a+b)^2 , a^2 – 2ab + b^2 = (a-b)^2 \)
② \(a^2 – b^2 = (a+b) (a-b) \)
③ \( x^2 + (a+b) x + ab = (x+a) (x+b)\)
④ \( acx^2 + (ad+bc) x + bd=(ax+b) (cx+d)\) ※たすきがけ
例題
次の式を因数分解せよ。
① \(x^2 + 12xy + 36y^2\)
② \(25a^2 – 9b^2 \)
③ \(x^2 +6x +5 \)
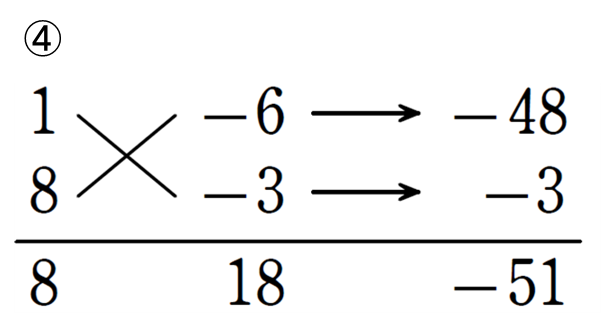
④ \( 8x^2-51x+18 \)
解答
① \(x^2 + 12xy + 36y^2\)
\(= x^2 + 2 \cdot x \cdot 6y + (6y)^2\)
\(=(x+6)^2 \)
② \(25a^2 – 9b^2 \)
\(=(5a)^2 – (3b)^2\)
\(= (5a+3b) (5a-3b) \)
③ \(x^2 +6x +5 \)
\(= x^2 + (1+5) x + 1 \cdot 5\)
\( = (x+1) (x+5)\)
④ \( 8x^2-51x+18\)
\(= (x-6) (8x-3)\)
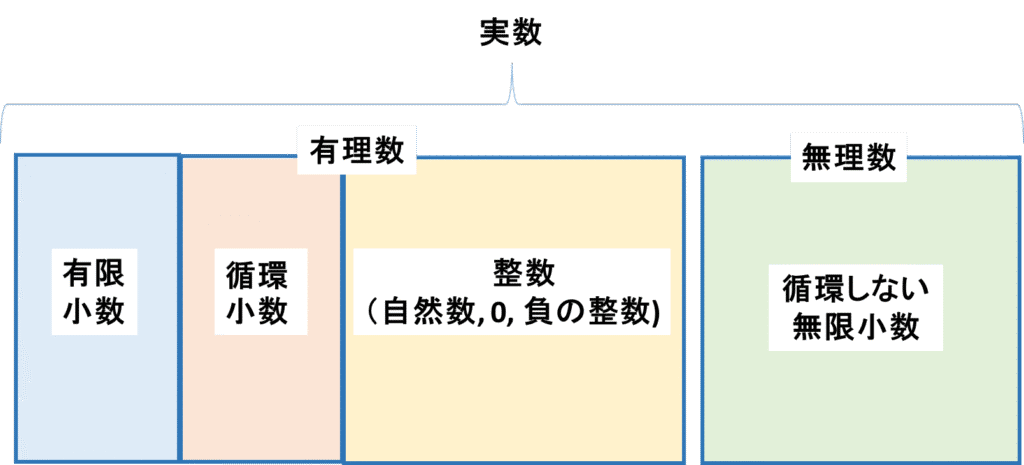
3.実数
例題
次の数の中から①自然数, ②整数, ③有理数, ④無理数 をそれぞれ選べ。
\(-2, 0, \displaystyle\frac{35}{5}, \displaystyle\frac{5}{2}, -\displaystyle\frac{7}{8},\)
\( -\sqrt{2}, \sqrt{16}, \displaystyle\frac{3}{\sqrt{3}}, (\sqrt{7})^2, \pi\)
解答
与えられた数において
\(-2\) (有理数かつ整数)
\(0\) (有理数かつ整数)
\(\displaystyle\frac{35}{5}=7\)(有理数かつ整数かつ自然数)
\(\displaystyle\frac{5}{2}=2.5\)(有限小数より、有理数)
\(-\displaystyle\frac{7}{8}=-0.875\)(有限小数より、有理数)
\(-\sqrt{2}=-1.4142 \cdots \)(循環しない無限小数より、無理数)
\(\sqrt{16}=4\)(有理数かつ整数かつ自然数)
\(\displaystyle\frac{3}{\sqrt{3}}=\sqrt{3}=1.732\cdots\)(循環しない無限小数より、無理数)
\((\sqrt{7})^2=7\) (有理数かつ整数かつ自然数)
\(\pi =3.141592 \cdots\)(循環しない無限小数より、無理数)
したがって、
① 自然数は \(\displaystyle\frac{35}{5}, \sqrt{16},(\sqrt{7})^2\)
② 整数は \(-2, 0, \displaystyle\frac{35}{5}, \sqrt{16}, (\sqrt{7})^2\)
③ 有理数は \(-2, 0, \displaystyle\frac{35}{5}, \displaystyle\frac{5}{2}, -\displaystyle\frac{7}{8}, \sqrt{16}, (\sqrt{7})^2\)
④ 無理数は \(-\sqrt{2}, \displaystyle\frac{3}{\sqrt{3}}, \pi \)
\( \begin{eqnarray} |x| = \begin{cases} x & (x \geq 0 のとき) \\ -x&(x \lt 0のとき) \end{cases}\end{eqnarray}\)
例題
次の値を求めよ。
① \(|-3|\)
② \(|3.7|\)
③ \(|\pi -4|\)
解答
① \(|-3| =-(-3)=3\)
② \(|3.7|=3.7\)
③ \(|\pi-4|=-(\pi-4)=-\pi+4\)
4.平方根
① \(a \geq 0\) のとき \((\sqrt{a})^2 =(- \sqrt{a})^2 = a, \sqrt{a} \geq 0 \)
② \( \begin{eqnarray} \sqrt{a^2}=|a| = \begin{cases} a & (a \geq 0 のとき) \\ -a&(a \lt 0のとき) \end{cases}\end{eqnarray}\)
例題
次の値を求めよ。
① \((-\sqrt{7})^2\)
② \(\sqrt{9}\)
解答
① \((-\sqrt{7})^2=7\)
② \(\sqrt{9}=\sqrt{3^2}=3\)
\(a>0, b>0, k>0 \) のとき
① \(\sqrt{a} \sqrt{b} = \sqrt{ab} \)
② \(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}} \)
③ \(\sqrt{k^2 a} = k \sqrt{a} \)
例題
次の値を求めよ。
① \(\sqrt{3}\sqrt{5}\)
② \(\frac{\sqrt{24}}{\sqrt{8}}\)
③ \(\sqrt{20}\)
解答
① \(\sqrt{3}\sqrt{5}=\sqrt{3 \cdot 5}=\sqrt{15}\)
② \(\frac{\sqrt{24}}{\sqrt{8}}=\sqrt{\frac{24}{8}}=\sqrt{3}\)
③ \(\sqrt{20}=\sqrt{2^2 \cdot 5}=2\sqrt{5}\)
5.1次不等式
① \(A < B \) ならば \(A+C < B+C, A-C < B-C\)
② \(A < B\) ならば
\(C>0\) のとき \(AC < BC, \frac{A}{C} < \frac{B}{C} \)
\(C<0\) のとき \(AC > BC, \frac{A}{C} > \frac{B}{C} \)
例題
\(a>b\) のとき,次の▢に適する不等号\(>\)または\(<\)を答えよ。
\(2a+1\) ▢ \(2b+1\)
\(3-5a\) ▢ \(3-5b\)
解答
① \(a>b\) の両辺を\(2\)倍すると
\(2a>2b\)
両辺を\(+1\)すると
\(2a+1>2b\)
よって \(>\)
② \(a>b\) の両辺を\(-5\)倍すると
\(-5a<-5b\)
両辺を\(+3\)すると
\(3-5a<3-5b\)
よって \(<\)
STEP① 不等式を \(ax > b, ax \leq b \) などの形に整理する。
STEP② 整理された不等式の両辺を \(x\) の係数 \(a\) で割る。
例題
不等式 \(-3x+2>23\) を解け。
解答
\(-3x+2>23\)
\(-3x>23-2\)
\(-3x>21\)
よって、
\(x<-7\)
STEP① それぞれの不等式を解く
STEP② 解いた不等式の共通範囲を求める
例題
次の連立不等式を解け。
\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 1 > 9 \\
3x + 5 \leq 32
\end{array}
\right.
\end{eqnarray}
解答
\(2x + 1 > 9\) を解くと
\(x > 4 \) ……①
\(3x + 5 \leq 32\)を解くと
\(x \leq 9\) ……②
①、②より
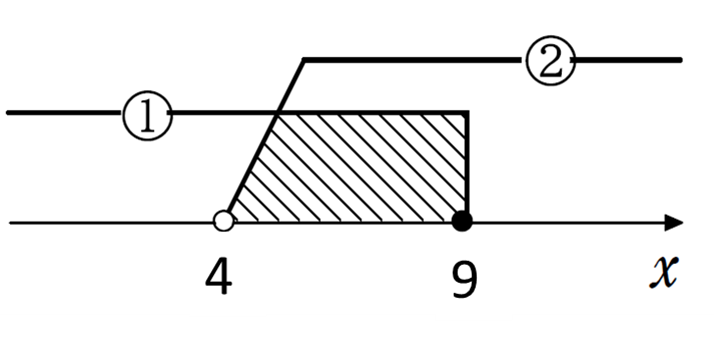
\(4 < x \leq 9\)
6.絶対値を含む方程式・不等式
\(c\) が正の定数のとき
① 方程式 \(|x|=c\) の解は \(x=\pm c \)
② 不等式 \(|x|<c\) の解は \(-c<x<c\)
③ 不等式 \(|x|>c\) の解は \(x<-c, c<x \)
例題
次の方程式・不等式を解け。
① \(|x|\)=2
② \(|x|<2\)
③ \(|x|>2\)
解答
① \(x=\pm 2 \)
② \(-2<x<2\)
③ \(x<-2, 2<x \)





コメント