数学検定準2級(1次計算技能検定)対策向け問題まとめページです。
過去問題分析より、出題されやすい問題と解答を単元別に一問一答式で出題しています。
数学検定準2級対策(1次計算技能検定)問題まとめ~一問一答式~

展開の基本公式
\((x + y)^2 – 3(2x – y)\) を展開して計算しなさい。
解答・解説
\((x + y)^2 – 3x(2x – y)\)
\(= x^2 + 2xy + y^2 – 6x^2 + 3xy\)
\(= -5x^2 +5xy + y^2\)
よって
\( \color{red}{-5x^2 +5xy + y^2}\)
\((a + 3)(2a -1) – 3a(a – 1)\) を展開して計算しなさい。
解答・解説
\((a + 3)(2a -1) – 3a(a – 1)\)
\(= 2a^2 – a + 6a -3 – 3a^2 + 3a\)
\(= -a^2 +8a -3 \)
よって
\(\color{red}{-a^2 +8a -3} \)
\((x + 3)(x – 5) – (3 – 2x)^2\) を展開して計算しなさい。
解答・解説
\((x + 3)(x – 5) – (3 – 2x)^2\)
\(= x^2 -2x -15 – (9 – 12x + 4x^2)\)
\(= x^2 -2x -15 – 9 +12x -4x^2\)
\(= -3x^2 +10x -24\)
よって
\( \color{red}{-3x^2 +10x -24}\)
\((3a + b)(-4a +5b) – (a + b)(a -b)\) を展開して計算しなさい。
解答・解説
\((3a + b)(-4a +5b) – (a + b)(a -b)\)
\(= -12a^2 + 15ab -4ab +5b^2 – (a^2 – b^2)\)
\(= -12a^2 +11ab + 5b^2 – a^2 + b^2\)
\(= -13a^2 +11ab + 6b^2\)
よって
\(\color{red}{-13a^2 +11ab + 6b^2}\)
\((2x + y)(2x – y ) – 4x(5 – x)\) を展開して計算しなさい。
解答・解説
\((2x + y)(2x – y ) – 4x(5 – x)\)
\(= 4x^2 – y^2 – 20x +4x^2\)
\(= 8x^2 – 20x – y^2\)
よって
\(\color{red}{8x^2 – 20x – y^2}\)
因数分解の基本公式
\(3x^2y – 9xy^2\) を因数分解しなさい。
解答・解説
\(3x^2y – 9xy^2\)
\(= 3xy(x -3y)\)
よって
\( \color{red}{3xy(x -3y)}\)
\(4x^2 + 12xy + 9y^2\) を因数分解しなさい。
解答・解説
\(4x^2 + 12xy + 9y^2\)
\(= (2x)^2 + 2\cdot (2x)\cdot (3y) + (3y)^2\)
\(= (2x +3y)^2\)
よって
\(\color{red}{(2x +3y)^2} \)
\(25x^2 – 16y^2\) を因数分解しなさい。
解答・解説
\(25x^2 – 16y^2\)
\(= (5x)^2 – (4y)^2\)
\(= (5x + 4y)(5x – 4y)\)
よって
\( \color{red}{(5x + 4y)(5x – 4y)}\)
\(a^2 -5ab +6b^2\) を因数分解しなさい。
解答・解説
\(a^2 -5ab +6b^2\)
\(= a^2 + (-3b-2b)\cdot a +(-3b)\cdot(-2b)\)
\(= (a – 3b)(a – 2b)\)
よって
\(\color{red}{ (a – 3b)(a – 2b)}\)
\(x^2 + xy – 20y^2 \) を因数分解しなさい。
解答・解説
\(x^2 + xy – 20y^2\)
\(= x^2 + (5y -4y)\cdot x + (5y)\cdot (-4y)\)
\(= (x+5y)(x-4y)\)
よって
\(\color{red}{(x+5y)(x-4y)}\)
ルートの計算
\(\sqrt{2} – \sqrt{18} +\sqrt{32}\) を計算しなさい。
解答・解説
\(\sqrt{2} – \sqrt{18} +\sqrt{32}\)
\(= \sqrt{2} – \sqrt{2 \cdot 3^2} +\sqrt{2 \cdot 4^2}\)
\(= \sqrt{2} – 3\sqrt{2} +4\sqrt{2}\)
\(= (1-3+4)\sqrt{2}\)
\(=2\sqrt{2}\)
よって
\( \color{red}{2\sqrt{2}}\)
\(\sqrt{5} \times \sqrt{10} \times \sqrt{45}\times \sqrt{2}\) を計算しなさい。
解答・解説
\(\sqrt{5} \times \sqrt{10} \times \sqrt{45}\times \sqrt{40}\)
\(=\sqrt{5} \times \sqrt{10} \times 3\sqrt{5}\times 2\sqrt{10}\)
\(=(\sqrt{5})^2 \times (\sqrt{10})^2 \times 3 \times 2 \)
\(=5 \times 10 \times 3 \times 2 \)
\(=300\)
よって
\(\color{red}{300} \)
\(-\displaystyle\frac{1}{\sqrt{3}} + \sqrt{27} + \displaystyle\frac{4}{\sqrt{3}}\) を計算しなさい。
解答・解説
\(-\displaystyle\frac{1}{\sqrt{3}} + \sqrt{27} + \displaystyle\frac{4}{\sqrt{3}}\)
\(=-\displaystyle\frac{\sqrt{3}}{3} + 3\sqrt{3} +\displaystyle\frac{4\sqrt{3}}{3} \)
\(= \displaystyle\frac{-\sqrt{3}+9\sqrt{3} + 4\sqrt{3}}{3}\)
\(= \displaystyle\frac{12\sqrt{3}}{3}\)
\(= 4\sqrt{3}\)
よって
\( \color{red}{4\sqrt{3}}\)
\(\sqrt{98} + \sqrt{8} -\sqrt{50}\) を計算しなさい。
解答・解説
\(\sqrt{98} + \sqrt{8} -\sqrt{50}\)
\(=7\sqrt{2} + 2\sqrt{2} -5\sqrt{2}\)
\(=4\sqrt{2} \)
よって
\(\color{red}{ 4\sqrt{2}}\)
\(\sqrt{7} \times \sqrt{21} \times \sqrt{12}\) を計算しなさい。
解答・解説
\(\sqrt{7} \times \sqrt{21} \times \sqrt{12}\)
\(= \sqrt{7} \times \sqrt{7 \cdot 3} \times 2\sqrt{3}\)
\(= (\sqrt{7})^2 \times (\sqrt{3})^2 \times 2\)
\(= 7 \times 3 \times 2\)
\(= 42\)
よって
\(\color{red}{42}\)
2次方程式の解
\(x^2 – 6x + 8 =0\) を解きなさい。
解答・解説
\(x^2 – 6x + 8 =0\)
\((x – 2)(x – 4) = 0\)
よって
\( \color{red}{x = 2, 4}\)
\(x^2 + x – 3 =0\) を解きなさい。
解答・解説
\(x^2 + x – 3 =0\)
\(x = \displaystyle\frac{-1 \pm \sqrt{1^2 – 4 \cdot 1 \cdot (-3)}}{2}\)
\(x = \displaystyle\frac{-1 \pm \sqrt{1 + 12}}{2}\)
よって
\(\color{red}{x = \displaystyle\frac{-1 \pm \sqrt{13}}{2}} \)
\(x^2 + 4x – 1 =0\) を解きなさい。
解答・解説
\(x = -2 \pm \sqrt{(-2)^2 – 1 \cdot (-1)}\)
よって
\( \color{red}{x = -2 \pm \sqrt{5}}\)
\(x^2 – 8 = 0\) を解きなさい。
解答・解説
\(x^2 – 8 = 0\)
\(x^2 = 8\)
\(x = \pm \sqrt{8}\)
よって
\(\color{red}{x = \pm 2\sqrt{2}}\)
\(x^2 – 6x + 9 = 0\) を解きなさい。
解答・解説
\(x^2 – 6x + 9 = 0\)
\((x – 3)^2 = 0\)
よって
\(\color{red}{x = 3}\)
関数\(y = ax^2\)
\(y\) は\(x\) の \(2\) 乗に比例し, \(x = 2\) のとき \(y = 8\) です。\(x = 3\) のときの \(y\) の値を求めなさい。
解答・解説
\(y\) は\(x\) の\(2\) 乗に比例するから
\(y = ax^2\)(\(a\):実数)
とおくと、
\(x = 2\) のとき \(y = 8\) より
\(8 = a \cdot 2^2 \)
\( a = 2\)
よって、\(y = 2x^2\) において
\(x = 3\) のとき
\(y = 2 \cdot 3^2\)
よって
\( \color{red}{y = 18}\)
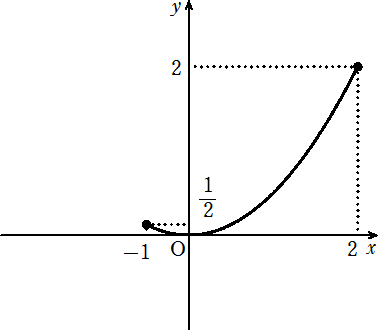
関数 \(y = \displaystyle\frac{1}{2}x^2\) において \(x\) の変域が \(-1 \leq x \leq 2\) のとき, \(y\) の変域を求めなさい。
解答・解説
\(x = -1\) のとき
\(y = \displaystyle\frac{1}{2}\cdot (-1)^2 =\displaystyle\frac{1}{2}\)
\(x = 2\) のとき
\(y = \displaystyle\frac{1}{2}\cdot 2^2 = 2\)
この関数のグラフは図のようになる
よって、\(y\) の変域は
\(\color{red}{0 \leq y \leq 2}\)
関数\(y = 3x^2\) において, \(x\) の値が \(-3\) から\(1\) まで増加するときの変化の割合を求めなさい。
解答・解説
\(x = -3\) のとき \(y = 3 \cdot (-3)^2 = 27\)
\(x = 1\) のとき \(y = 3 \cdot 1^2 = 3\)
よって
\(\displaystyle\frac{3 – 27}{1 – (-3)} = \displaystyle\frac{-24}{4} = -6 \)
より
\( \color{red}{-6}\)
\(y\) は\(x\) の\(2\)乗に比例し, \(x = 1\) のとき\(y = -5\) です。\(x = -2\) のときの\(y\) の値を求めなさい。
解答・解説
\(y\) は\(x\) の2乗に比例するから
\(y = ax^2\)(\(a\):実数)
とおくと、
\(x = 1\) のとき\(y = -5\)より
\(-5 = a \cdot 1^2 \)
\( a = -5\)
よって、\(y = -5x^2\) において
\(x = -2\)のとき
\(y = -5 \cdot (-2)^2\)
よって
\(\color{red}{y = -20}\)
関数\(y = -x^2\) において, \(x\) の値が \(2\) から\(4\) まで増加するときの変化の割合を求めなさい。
解答・解説
\(x = 2\) のとき\(y = – 1\cdot 2^2 = – 4\)
\(x = 4\) のとき\(y = – 1\cdot 4^2 = -16\)
よって
\(\displaystyle\frac{-16 – (-4)}{4 – 2} = \displaystyle\frac{-12}{2} = -6\)
より
\(\color{red}{-6}\)
相似比
次の図の△ABC において, \(DE /\!/ BC\)のとき, \(x\) の値を求めなさい。
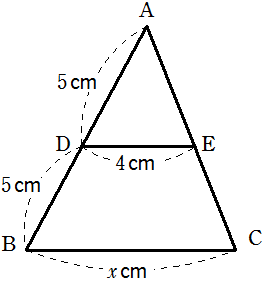
解答・解説
\(DE /\!/ BC\) のとき
△ABC∽△ADE より
AB : AD = BC : DE より,
\(10 : 5 = x : 4\)
\(5x = 40\)
\(\color{red}{x = 8}\)
2つの三角形 \(X\) と\(Y\) は相似で相似比は\(5 : 6\) です。三角形 \(X\) の周の長さが\(25\)cm のとき、
三角形 \(Y\) の周の長さを求めなさい。
解答・解説
三角形\(Y\) の周の長さを\(x\) cm とすると
相似比が \(5 : 6\) より
\(25 : x = 5 : 6\)
よって
\(5x = 25 \times 6\)
\(5x = 150\)
\(\color{red}{x = 30}\)
次の図において, \(AB /\!/ CD /\!/ EF\) のとき, \(x\) の値を求めなさい。
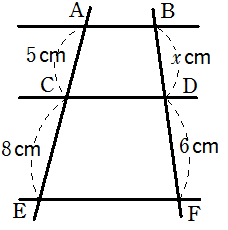
解答・解説
\(AB /\!/ CD /\!/ EF\) のとき
\(5 : 8 = x : 6\)
よって
\(8x = 30\)
\(\color{red}{x = \displaystyle\frac{15}{4}}\)
次の図の△ABC において, \(DE /\!/ BC\)のとき, \(x\) の値を求めなさい。
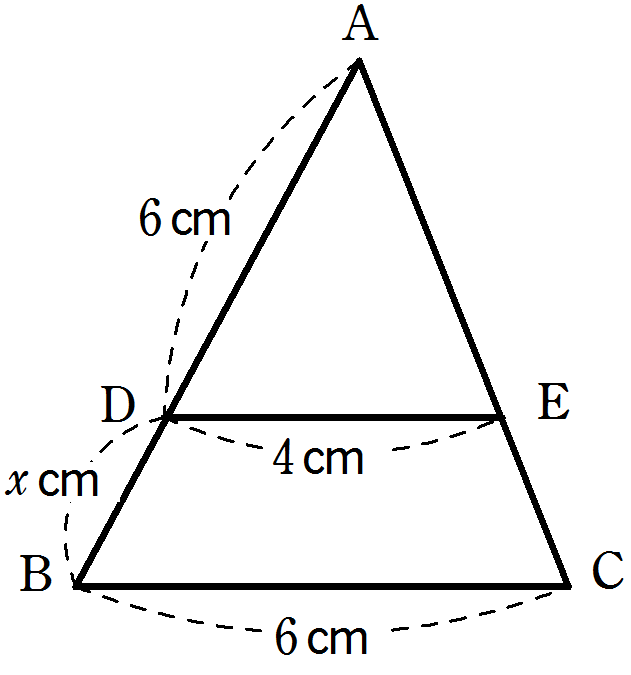
解答・解説
\(DE /\!/ BC\) のとき
△ABC∽△ADE より
AB : AD = BC : DE より,
\(x + 6 : 6 = 6 : 4\)
\(4(x + 6) = 36\)
\(x +6 = 9\)
\(\color{red}{x = 3}\)
2つの三角形 \(X\) と\(Y\) は相似で相似比は\(2 : 3\) です。三角形 \(Y\) の周の長さが\(12\) cm のとき、
三角形 \(X\) の周の長さを求めなさい。
解答・解説
三角形\(X\) の周の長さを\(x\) cm とすると
相似比が \(2 : 3\) より
\(x : 12 = 2 : 3\)
よって
\(3x = 12 \times 2\)
\(3x = 24\)
\(\color{red}{x = 8}\)
三平方の定理
右の図の直角三角形において、\(x\) の値を求めなさい。
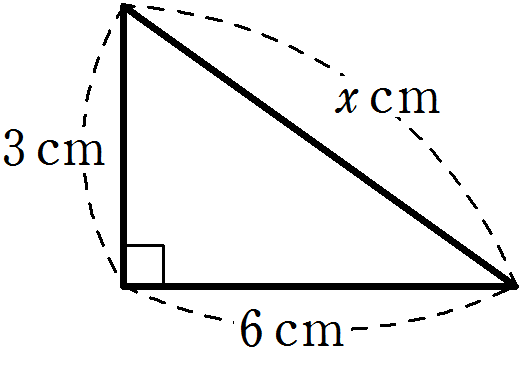
解答・解説
三平方の定理より
\(x = \sqrt{3^2 + 6^2}\)
\(x = \sqrt{45}\)
\(\color{red}{x = 3\sqrt{5}}\)
右の図の直角三角形において、\(x\) の値を求めなさい。
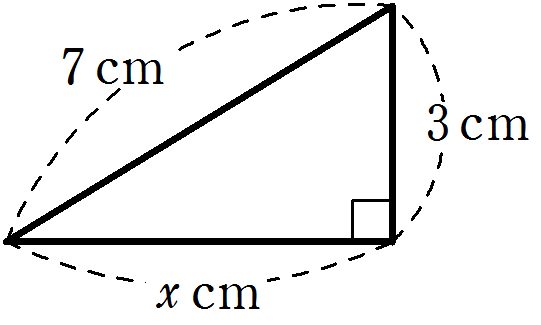
解答・解説
三平方の定理より
\(x = \sqrt{7^2 – 3^2}\)
\(= \sqrt{40}\)
\(\color{red}{x = 2\sqrt{10}}\)
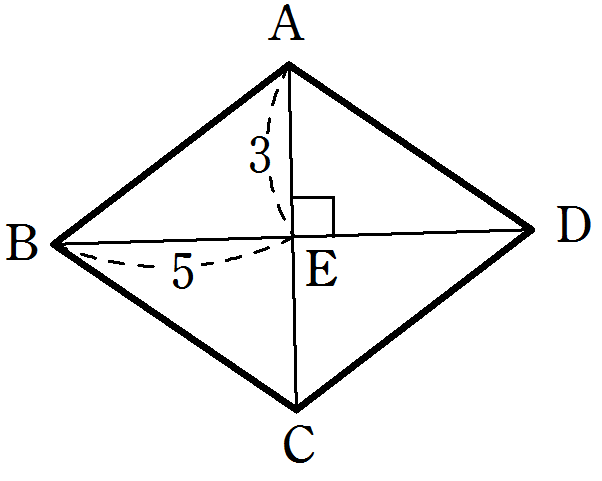
2本の対角線の長さがそれぞれ\(6\) cm, \(10\) cm であるひし形があります。このひし形の一辺の長さを求めなさい。
解答・解説
図のような\(BD = 10\), \(AC = 6\)であるひし形において
\(AC, BD\) の交点を \(E\) とすると 、
ひし形の対角線はそれぞれの中点で垂直に交わるから、
\(△ABE\) は
\(BE = 5\), \(AE = 3\), \(∠AEB = 90^{\circ}\)の直角三角形である。
したがって、三平方の定理より
\(AB = \sqrt{5^2 + 3^2} =\sqrt{34}\)
\(\color{red}{\sqrt{34}}\)cm
展開の応用
\((x^2 – 3x +1)^2\) を展開して計算しなさい。
解答・解説
\((x^2 – 3x +1)^2\)
\(= (x^2)^2 + (-3x)^2 + 1^2 + 2\cdot (x^2) \cdot (-3x) + 2\cdot (-3x) \cdot 1 + 2\cdot 1 \cdot (x^2)\)
\(= x^4 + 9x^2 + 1 – 6x^3 – 6x + 2x^2\)
\(= x^4 – 6x^3 + 11x^2 – 6x +1\)
よって
\( \color{red}{x^4 – 6x^3 + 11x^2 – 6x +1}\)
\((a^2 – 3a +1)^2\) を展開して計算しなさい。
解答・解説
\((a^2 + 2a – 3)^2\)
\(= (a^2)^2 + (2x)^2 + (-3)^2 + 2\cdot (a^2) \cdot (2a) + 2\cdot (2a) \cdot (-3) + 2\cdot (-3) \cdot (a^2)\)
\(= a^4 + 4a^2 + 9 + 4a^3 – 12a – 6a^2\)
\(= a^4 + 4a^3 – 2a^2 – 12a + 9\)
よって
\( \color{red}{a^4 + 4a^3 – 2a^2 – 12a + 9}\)
\((x^2 + 2x + 7)(x^2 – 2x + 7)\) を展開して計算しなさい。
解答・解説
\((x^2 + 2x + 7)(x^2 – 2x + 7)\)
\(= \{(x^2 + 7) + 2x\}\{(x^2 + 7) – 2x\}\)
\(= (x^2 + 7)^2 – (2x)^2\)
\(= (x^4 + 14x^2 +49) – 4x^2\)
\(= x^4 + 10x^2 +49\)
よって
\( \color{red}{x^4 + 10x^2 +49}\)
因数分解の応用
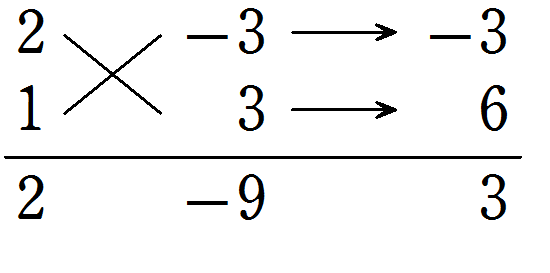
\(3x^2 -4xy – 4y^2\) を因数分解しなさい。
解答・解説
たすき掛けは次のようになる
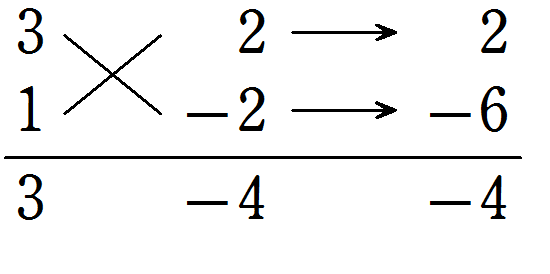
したがって
\( \color{red}{(3x + 2y)(x – 2y)}\)
\(2a^2 + 3ab – 9b^2\) を因数分解しなさい。
解答・解説
たすき掛けは次のようになる
したがって
\(\color{red}{(2a – 3b)(a + 3b)} \)
\(2a^2 b + a^2 + 4b – 4\) を因数分解しなさい。
解答・解説
\(2a^2 b + a^2 – 8b – 4\)
\(= 2a^2 b – 8b + a^2 – 4\)
\(= 2b (a^2 – 4) + (a^2 – 4) \)
\(= (a^2 – 4)(2b + 1) \)
\(= (a + 2)(a – 2)(2b + 1) \)
よって
\( \color{red}{(a + 2)(a – 2)(2b + 1)}\)
分母の有理化
\(\displaystyle\frac{3}{\sqrt{5} – \sqrt{2}} + \displaystyle\frac{3}{\sqrt{5} + \sqrt{2}}\) を計算しなさい。
解答・解説
\(\displaystyle\frac{3}{\sqrt{5} – \sqrt{2}} \times \displaystyle\frac{\sqrt{5} + \sqrt{2}}{\sqrt{5} + \sqrt{2}}\)
\(=\displaystyle\frac{3(\sqrt{5} + \sqrt{2})}{5 – 2}\)
\(= \sqrt{5} + \sqrt{2}\)
\(\displaystyle\frac{3}{\sqrt{5} + \sqrt{2}} \times \displaystyle\frac{\sqrt{5} – \sqrt{2}}{\sqrt{5} – \sqrt{2}}\)
\(=\displaystyle\frac{3(\sqrt{5} – \sqrt{2})}{5 – 2}\)
\(= \sqrt{5} – \sqrt{2}\)
よって
与式)
\( = (\sqrt{5} + \sqrt{2}) + (\sqrt{5} – \sqrt{2}) \)
\( = \color{red}{2\sqrt{5}}\)
\(\displaystyle\frac{2}{\sqrt{11} – 3} – \sqrt{11} \) を計算しなさい。
解答・解説
\(\displaystyle\frac{2}{\sqrt{11} – 3}\)
\(= \displaystyle\frac{2}{\sqrt{11} – 3} \times \displaystyle\frac{\sqrt{11} + 3}{\sqrt{11} + 3}\)
\(= \displaystyle\frac{2(\sqrt{11} + 3)}{11 – 9}\)
\(= \sqrt{11} + 3\)
よって
(与式)
\(= (\sqrt{11} + 3) – \sqrt{11}\)
\(= \color{red}{3}\)
\(\displaystyle\frac{10}{\sqrt{15} + 5} + \sqrt{15} \) を計算しなさい。
解答・解説
\(\displaystyle\frac{10}{\sqrt{15} + 5}\)
\(= \displaystyle\frac{10}{\sqrt{15} + 5} \times \displaystyle\frac{\sqrt{15} – 5}{\sqrt{15} – 5}\)
\(= \displaystyle\frac{10(\sqrt{15} – 5)}{15 – 25}\)
\(= – (\sqrt{15} – 5\)
\(= – \sqrt{15} + 5\)
よって
(与式)
\(= (- \sqrt{15} + 5) + \sqrt{15} \)
\(= \color{red}{5}\)
2次不等式の解
2次不等式\(x^2 – 10x +9 < 0\) を解きなさい。
解答・解説
\((x – 1)(x – 9) < 0\)
よって
\(\color{red}{1 < x < 9}\)
2次不等式\(x^2 – 2x – 3 > 0\) を解きなさい。
解答・解説
\((x + 1)(x -3) > 0\)
よって
\(\color{red}{x < -1, 3 < x}\)
2次不等式\(x^2 – 8x – 48 > 0\) を解きなさい。
解答・解説
\((x + 4)(x – 12) > 0\)
よって
\(\color{red}{x < -4, 12 < x}\)
2次関数
放物線 \( y = x^2 – 6x + 7\) の頂点の座標を求めなさい。
解答・解説
\(y = x^2 – 6x + 7\)
\(= (x – 3)^2 – 9 + 7\)
\(= (x – 3)^2 – 2\)
よって
\(\color{red}{頂点(3, -2)}\)
放物線 \( y = x^2 + 8x + 17\) の頂点の座標を求めなさい。
解答・解説
\( y = x^2 + 8x + 17\)
\(= (x + 4)^2 -16 +17\)
\(= (x + 4)^2 + 1\)
よって
\(\color{red}{頂点(-4, 1)}\)
\(k\) を定数とします。放物線\( y = \displaystyle\frac{1}{2}x^2 + (k -1)x – 3k + 2\) が点\((2, 1)\) を通るとき, \(k\) の値を求めなさい。
解答・解説
放物線\( y = \displaystyle\frac{1}{2}x^2 + (k -1)x – 3k + 2\) が点\((2, -3)\) を通るから
\(-3 = \displaystyle\frac{1}{2} \cdot 2^2 + (k -1) \cdot 2 – 3k + 2\)
\(-3 = 2 + 2k – 2 – 3k + 2\)
\(-3 = – k + 2\)
よって
\(\color{red}{k = 5}\)
1次不等式の応用
不等式 \(1.2x – 0.8 < 3 + x\) を求めなさい。
解答・解説
両辺を\(10\) 倍すると
\(12x – 8 < 30 + 10x\)
\(12x – 10x < 30 + 8\)
\(2x < 38\)
\(x < 19\)
よって
\(\color{red}{x < 19}\)
不等式 \(\displaystyle\frac{1}{2}x – 2 > \displaystyle\frac{2}{3}x + 3\) を求めなさい。
解答・解説
両辺を\(6\) 倍すると
\(3x – 12 < 4x + 18\)
\(3x – 4x < 18 + 12\)
\(-x < 30\)
\(x > -30\)
よって
\(\color{red}{x > -30}\)
不等式 \(\displaystyle\frac{1}{5}x + 2 > \displaystyle\frac{7}{10}x – 3\) を求めなさい。
解答・解説
両辺を\(10\) 倍すると
\(2x + 20 > 7x – 30\)
\(2x – 7x < -30 – 20\)
\(- 5x < -50\)
\(x > 10\)
よって
\(\color{red}{x > 10}\)
\(n\) 進法
\(2\) 進法で表された数\(11101_{(2)}\) を\(10\) 進法で表しなさい。
解答・解説
\(11101_{(2)}\)
\(=1 \cdot 2^4 + 1 \cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 1 \cdot 1\)
\(=16 + 8 + 4 + 1\)
\(=29\)
よって
\(\color{red}{29}\)
\(3\) 進法で表された数\(12012_{(3)}\) を\(10\) 進法で表しなさい。
解答・解説
\(12012_{(3)}\)
\(=1 \cdot 3^4 + 2 \cdot 3^3 + 0 \cdot 3^2 + 1 \cdot 3^1 + 2 \cdot 1\)
\(=81 + 54 + 3 + 2\)
\(=140\)
よって
\(\color{red}{140}\)
\(5\) 進法で表された数\(2123_{(5)}\) を\(10\) 進法で表しなさい。
解答・解説
\(2123_{(5)}\)
\(=2 \cdot 5^3 + 1 \cdot 5^2 + 2 \cdot 5^1 + 3 \cdot 1\)
\(=250 + 25 + 10 + 3\)
\(=288\)
よって
\(\color{red}{288}\)
図形の性質
次の図の△ABC において, \(3\) 点\(P, Q, R\) は
それぞれ辺\(BC, CA, AB\)上の点です。
\(3\) つの線分\(AP, PQ, CR\) が1点\(O\) で交わるとき,
\(AR:RB\) を最も簡単な整数の比で表しなさい。
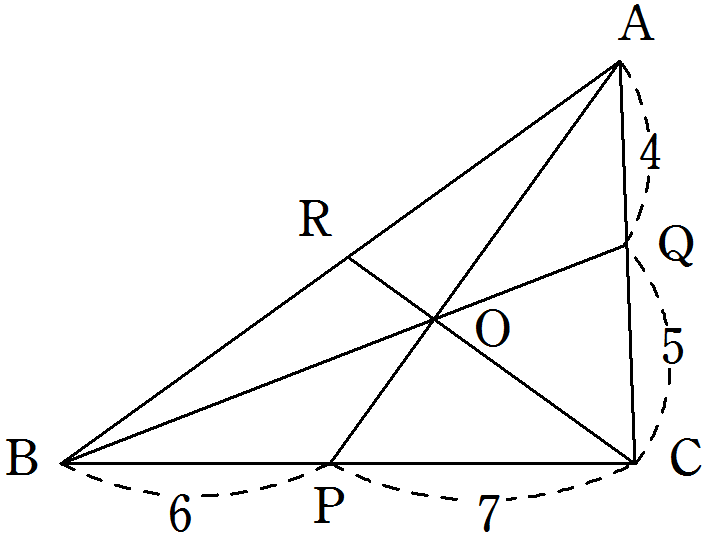
解答・解説
△ABC においてチェバの定理より
\(\displaystyle\frac{RB}{AR} \times \displaystyle\frac{PC}{BP} \times \displaystyle\frac{QA}{CQ} =1 \)
\(\displaystyle\frac{RB}{AR} \times \displaystyle\frac{7}{6} \times \displaystyle\frac{4}{5} =1 \)
\(\displaystyle\frac{RB}{AR} = \displaystyle\frac{15}{14} \)
したがって、
\(\color{red}{AR : RB = 14 : 15}\)
右の図のように,四角形ABCDが円に内接し,
\(\angle\mathrm{ADC} = 127^{\circ}\) です。
このとき,
\(\angle\mathrm{\alpha}\)の大きさを求めなさい。
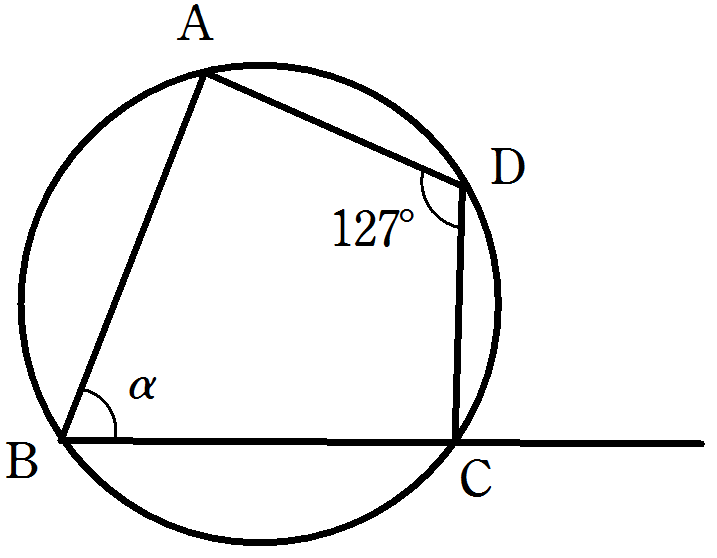
解答・解説
四角形ABCDは円に内接しているので
\(\alpha + 127 = 180\)
よって
\(\color{red}{\alpha = 53^{\circ}}\)
右の図のように,四角形ABCDが円に内接し,
\(\angle\mathrm{BAD} = 113^{\circ}\)です。
このとき,
\(\angle\mathrm{\alpha}\)
の大きさを求めなさい。
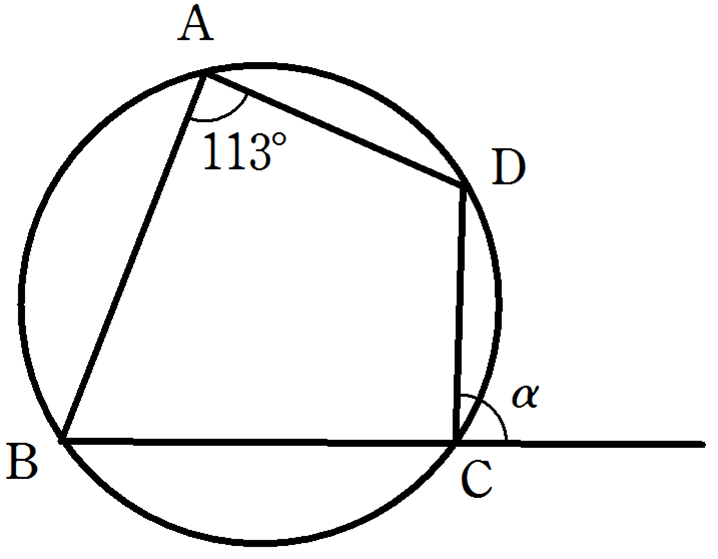
解答・解説
四角形ABCDは円に内接しているので
\(\alpha = \angle\mathrm{BAD} = 113^{\circ}\)
よって
\(\color{red}{\alpha = 113^{\circ}}\)
三角比の相互関係
\(90^{\circ} < \theta < 180^{\circ}\) で \(\sin\theta = \displaystyle\frac{3}{5}\) のとき、\(\cos\theta\) の値を求めなさい。
解答・解説
\(\sin^2 \theta + \cos^2 \theta = 1\) より
\(\cos^2 \theta = 1 – \sin^2 \theta\)
\(= 1 – \left(\displaystyle\frac{3}{5} \right)^2 \)
\(= 1 – \left(\displaystyle\frac{9}{25} \right)\)
\(= \displaystyle\frac{16}{25} \)
\(\cos\theta = \pm \sqrt{\displaystyle\frac{16}{25}} = \pm \displaystyle\frac{4}{5} \)
\(90^{\circ} < \theta < 180^{\circ}\) のとき, \(\cos\theta < 0 \)であるから
\( \color{red}{\cos\theta = -\displaystyle\frac{4}{5} }\)
\(90^{\circ} < \theta < 180^{\circ}\) で \(\sin\theta = \displaystyle\frac{1}{8}\) のとき、\(\cos\theta\) の値を求めなさい。
解答・解説
\(\sin^2 \theta + \cos^2 \theta = 1\) より
\(\cos^2 \theta = 1 – \sin^2 \theta\)
\(= 1 – \left(\displaystyle\frac{1}{8} \right)^2 \)
\(= 1 – \left(\displaystyle\frac{1}{64} \right)\)
\(= \displaystyle\frac{63}{64} \)
\(\cos\theta = \pm \sqrt{\displaystyle\frac{63}{64}} = \pm \displaystyle\frac{3\sqrt{7}}{8}\)
\(90^{\circ} < \theta < 180^{\circ}\) のとき, \(\cos\theta < 0 \)であるから
\( \color{red}{\cos\theta = -\displaystyle\frac{3\sqrt{7}}{8} }\)
\(0^{\circ} < \theta < 180^{\circ}\) で \(\cos\theta = -\displaystyle\frac{2}{3}\) のとき、\(\sin\theta\) の値を求めなさい。
解答・解説
\(\sin^2 \theta + \cos^2 \theta = 1\) より
\(\sin^2 \theta = 1 – \cos^2 \theta\)
\(= 1 – \left(\displaystyle\frac{2}{3} \right)^2 \)
\(= 1 – \left(\displaystyle\frac{4}{9} \right)\)
\(= \displaystyle\frac{5}{9} \)
\(\sin\theta = \pm \sqrt{\displaystyle\frac{5}{9}} = \pm \displaystyle\frac{\sqrt{5}}{3}\)
\(0^{\circ} < \theta < 180^{\circ}\) のとき, \(\sin\theta > 0 \)であるから
\( \color{red}{\sin\theta = \displaystyle\frac{\sqrt{5}}{3} }\)
\(\sin\theta = \displaystyle\frac{3}{5}\), \(\cos\theta = -\displaystyle\frac{4}{5}\) のとき、\(\tan\theta\) の値を求めなさい。
解答・解説
\(\tan\theta = \displaystyle\frac{\sin\theta}{\cos\theta}\) より
\(\tan\theta = \displaystyle\frac{\displaystyle\frac{3}{5}}{ – \displaystyle\frac{4}{5}}\)\(= – \displaystyle\frac{3}{4}\)
よって
\( \color{red}{\tan\theta = – \displaystyle\frac{3}{4} }\)
\(\sin\theta = \displaystyle\frac{\sqrt{5}}{3}\), \(\cos\theta = -\displaystyle\frac{2}{3}\) のとき、\(\tan\theta\) の値を求めなさい。
解答・解説
\(\tan\theta = \displaystyle\frac{\sin\theta}{\cos\theta}\) より
\(\tan\theta = \displaystyle\frac{\displaystyle\frac{\sqrt{5}}{3}}{ -\displaystyle\frac{2}{3}}\)\(= – \displaystyle\frac{\sqrt{5}}{2}\)
よって
\( \color{red}{\tan\theta = – \displaystyle\frac{\sqrt{5}}{2} }\)
集合
2つの集合 \(A = \{1, 2, 5, 6\}, B = \{2, 6, 7\}\) において、集合 \(A\cap B\) を要素を書き並べる方法で表しなさい。
解答・解説
\(A\cap B\) は集合\(A\) ,集合\(B\) の共通部分 (\(A\) かつ \(B\) )より
\(\color{red}{A\cap B = \{2, 6\}}\)
2つの集合 \(A = \{1, 2, 5, 6\}, B = \{2, 6, 7\}\) において、集合 \(A\cup B\) を要素を書き並べる方法で表しなさい。
解答・解説
\(A\cup B\) は集合\(A\) ,集合\(B\) の和集合(\(A\) または \(B\) )より
\(\color{red}{A\cup B = \{1, 2, 5, 6, 7\}}\)
2つの集合 \(A = \{1, 2, 3, 5, 6, 8\}, B = \{1, 2, 6, 7\}\) において、集合 \(A\cup B\) を要素の個数を求めなさい。
解答・解説
\(A\cup B\) は集合\(A\) ,集合\(B\) の和集合 (\(A\) または \(B\) )より
\(A\cup B = \{1, 2, 3, 5, 6, 7, 8 \}\)
よって、要素の個数は
\(\color{red}{7個}\)
順列(Pの計算)
\({}_6 \mathrm{P}_{2}\) の値を求めなさい。
解答・解説
\({}_6 \mathrm{P}_{2}\)
\(= 6 \cdot 5\)
\(= 30\)
よって
\(\color{red}{30}\)
\({}_8 \mathrm{P}_{3}\) の値を求めなさい。
解答・解説
\({}_8\mathrm{P}_{3}\)
\(= 8 \cdot 7 \cdot 6\)
\(= 336\)
よって
\(\color{red}{336}\)
\({}_5 \mathrm{P}_{4}\) の値を求めなさい。
解答・解説
\({}_5 \mathrm{P}_{4}\)
\(= 5 \cdot 4 \cdot 3 \cdot 2\)
\(= 120\)
よって
\(\color{red}{120}\)
組合せ(Cの計算)
\({}_6 \mathrm{C}_{2}\) の値を求めなさい。
解答・解説
\({}_6 \mathrm{C}_{2}\)
\(= \displaystyle\frac{6 \cdot 5}{2 \cdot 1}\)
\(= 15\)
よって
\(\color{red}{15}\)
\({}_8 \mathrm{C}_{3}\) の値を求めなさい。
解答・解説
\({}_8 \mathrm{C}_{3}\)
\(= \displaystyle\frac{8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1}\)
\(= 56\)
よって
\(\color{red}{56}\)
\({}_{30} \mathrm{C}_{28}\) の値を求めなさい。
解答・解説
\({}_{30} \mathrm{C}_{28}\)
\(= {}_{30} \mathrm{C}_{30 – 28}\)
\({}_{30} \mathrm{C}_{2}\)
\(= \displaystyle\frac{30 \cdot 29}{2 \cdot 1}\)
\(= 435\)
よって
\(\color{red}{435}\)
一問一答式の後は数学検定準2級(1次計算技能検定)の過去問題を解こう!

上記の一問一答式が終わったら、実際の過去問題にチャレンジしましょう!
過去に数学検定準2級(1次計算技能検定)で出題された問題から分析したオリジナル対策問題を以下で公開しています。
以下の3回分の問題を解くことで過去問対策になります。
オリジナル対策問題と解説が無料でダウンロードできます
対策問題一覧はこちら




コメント